Минимизация логических выражений
Теперь вы знаете, как формируется сумма произведений для произвольной таблицы истинности. Фактически для каждой таблицы истинности существует множество эквивалентных выражений и логических схем. Два логических выражения или две логические схемы считаются эквивалентными, если у них одинаковые таблицы истинности. Сформированной нами в предыдущем разделе сумма произведений для функции f1 эквивалентно, в частности, такое выражение:

 +
+ 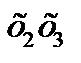
Чтобы это доказать, достаточно составить таблицу истинности данного выражения и сравнить ее с таблицей 3.2. Процесс создания таблицы истинности выражения 
 + х2х3, приведенной в табл. 3.3, можно разбить на три этапа. Сначала для каждого набора входных значений вычисляется произведение
+ х2х3, приведенной в табл. 3.3, можно разбить на три этапа. Сначала для каждого набора входных значений вычисляется произведение 
 , затем — произведение х2х3, после чего оба результата складываются для получения окончательного значения. Как видите, наша таблица истинности идентична таблице истинности функции f1, приведенной в табл. 3.2.
, затем — произведение х2х3, после чего оба результата складываются для получения окончательного значения. Как видите, наша таблица истинности идентична таблице истинности функции f1, приведенной в табл. 3.2.
Для упрощения логических выражений выполняется ряд алгебраических операций. Они основаны на двух логических законах, о которых мы еще не упоминали: дистрибутивном
w(y + z) = wy + wz
и законе исключенного третьего:
w + 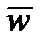 = 1
= 1
Таблица 3.3. Вычисление выражения 
 + х2х3
+ х2х3
| x1 x2 x3 |  
| х2х3 |   + х2х3 = f1 + х2х3 = f1
|
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Таблица 3.4. Использование таблиц истинности для доказательства эквивалентности выражений.
| w у z | y + z | Значение w(y + z) | wy | wz | Значение wy + wz |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
В табл. 3.4. приведено доказательство истинности дистрибутивного закона. Очевидно, что подобные законы всегда можно доказать с помощью таблиц истинности выражений, стоящих справа и слева от знака равенства. Совпадение результирующих значений в этих двух таблицах подтверждает проверяемый закон, логические законы, подобные дистрибутивному, иногда называют тождествами.
Вот еще одна форма дистрибутивного закона, которую мы приводим для полноты изложения материала, хотя она нам и не потребуется:
w +yz = (w+y)(w + z)
Целью минимизации логического выражения, представляющего заданную логическую функцию, является уменьшение стоимости ее реализации (количества используемых логических элементов). Общая схема процесса реализации логической функции такова. Сначала по описанному нами алгоритму для нее составляется сумма произведений (дизъюнктивная совершенная нормальная форма). Затем полученное выражение минимизируют до эквивалентной минимальной суммы произведений. Чтобы определить критерий минимизации, нужно ввести понятие стоимости, или величины, логического выражения.
Обычно при оценке стоимости выражения учитывается общее количество вентилей и их входных значений (входных линий), необходимых для реализации выражения в форме, показанной на рис. 3.11. Например, стоимость большей схемы на этом рисунке равна 21: 5 вентилей плюс 16 входных значений. Инверсия входных значений при подсчете игнорируется. Стоимость более простого выражения равна 9:3 вентиля плюс 6 входных значений. Теперь можно определить и критерий минимизации. Сумма произведений считается минимальной, если не существует эквивалентного ей выражения меньшей стоимости. В простых примерах, которые мы будем рассматривать в этой книге, минимальный размер выражений будет очевидным. Поэтому мы не считаем нужным приводить строгие доказательства их минимальности.
Стратегия упрощения заданного выражения заключается в следующем. Прежде всего термы-произведения разбиваются на пары, отличающиеся единой переменной, которая в одном терме дополняется ( 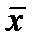 ), а во втором используется как есть (х). Затем в каждой паре общее произведение двух переменных выносится за скобки, а в скобках остается терм х+
), а во втором используется как есть (х). Затем в каждой паре общее произведение двух переменных выносится за скобки, а в скобках остается терм х+ 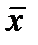 , всегда равный 1. Вот что мы получим, применив эту процедуру к первому выражению для функции f1:
, всегда равный 1. Вот что мы получим, применив эту процедуру к первому выражению для функции f1:
f1 = 

 +
+ 
 х3 +
х3 +  х2х3 + x1х2х3 =
х2х3 + x1х2х3 = 
 (
(  + х3) + (
+ х3) + (  +x1) х2х3 =
+x1) х2х3 = 
 ×1 + 1× х2х3 =
×1 + 1× х2х3 = 
 + х2х3
+ х2х3
Это выражение минимально. Соответствующая ему логическая схема приведена на уже упоминаемом нами рис. 3.11.
Сгруппировать термы попарно, с тем чтобы упростить исходное выражение, не всегда так просто, как в примере с функцией f1. В случае затруднений помогает такое правило:
w + w = w
Это правило позволяет повторять термы-произведения при необходимости объединить некоторый терм более чем с одним другим термом. Для примера рассмотрим функцию f2 из табл. 3.1. Исходная сума произведений, формируемая на основе таблицы истинности этой функции, такова:
f2 = 

 +
+ 
 х3 +
х3 +  х2
х2  + x1
+ x1 
 + x1
+ x1  х3
х3
Повторив первый терм 

 и изменив порядок следования термов (на основе коммутативного закона), мы получим:
и изменив порядок следования термов (на основе коммутативного закона), мы получим:
f2 = 

 +
+ 
 х3 + x1
х3 + x1 
 + x1
+ x1  х3 +
х3 + 

 +
+  х2
х2 
Сгруппировав термы попарно и вынеся одинаковые произведения за скобки, сможем записать следующее выражение:
f2 = 
 (
(  + х3) + x1
+ х3) + x1  (
(  + х3) +
+ х3) +  (
(  + х2)
+ х2)  =
= 
 + x1
+ x1  +
+ 

Первую пару термов можно упростить еще раз, и тогда получится минимальное выражение:
f2 =  +
+ 

На этом обсуждение способов алгебраического упрощения логических выражений завершается. Данное математическое упражнение еще раз доказывает, что ее простые логические схемы, содержащие меньше вентилей и входных значений, легче и дешевле реализовать на практике. Так что стремление минимизировать логические выражения имеет под собой чисто экономическое основание. Законы, которые мы с вами использовали для манипулирования логическими выражениями, объединены в табл. 3.5. Они приведены парами, чтобы видна была симметрия функций И и ИЛИ. До сих пор нам не представилось случая воспользоваться законами возведения в степень и де Моргана, но в следующих разделах они нам пригодятся.
Таблица 3.5. Законы двоичной логики
| Название закона | Алгебраическое тождество | |
| Коммутативный Ассоциативный Дистрибутивный Идемпотентности Возведение в степень Дополнения (закон исключенного третьего) Закон де Моргана | w + у = у + w
(w + у) + z = у + (w + z)
w + yz = (w + y)(w + z)
w + w = w
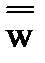 = w
w + = w
w + 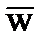 = 1
( = 1
( 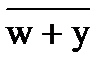 ) = wy
0 + w = w
1•w=1 ) = wy
0 + w = w
1•w=1
| wу = yw
(wy)z = w(yz)
w(y + z) = wy + wz
ww= w
w 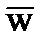 = 0 = 0
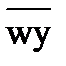 = = 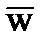 + + 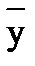 0•w = 0
1•w
0•w = 0
1•w
|
| Название закона | Алгебраическое тождество | |
| Коммутативный | w + у = у + w | wу = yw |
| Ассоциативный | (w + у) + z = у + (w + z) | (wy)z = w(yz) |
| Дистрибутивный | w + yz = (w + y)(w + z) | w(y + z) = wy + wz |
| Идемпотентности | w + w = w | ww= w |
| Закон исключенного третьего / закон противоречия | w + 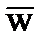 = 1 = 1
| w 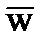 = 0 = 0
|
| Закон де Моргана | ( 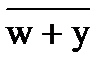 ) = wy ) = wy
| 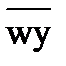 = = 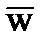 + + 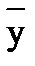
|
| Законы исключения констант | 0 + w = w | 0•w = 0 |
| 1+w=1 | 1•w=w | |
| Возведение в степень | 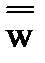 = w = w
|
Лекция 11
Дата добавления: 2016-07-05; просмотров: 3958;











