Синтез вентилей И-НЕ и ИЛИ-НЕ

А сейчас нам предстоит рассмотреть еще два базовых логических вентиля, называемых И-НЕ и ИЛИ-НЕ. Эти вентили очень широко применяются в логических схемах, что объясняется простотой их реализации. Таблицы истинности вентилей И-НЕ и ИЛИ-НЕ приведены на рис. А.7. Они представляют собой функции И и ИЛИ, к результату которых применена функция НЕ. Если мы обозначим операторы И-НЕ и ИЛИ-НЕ символами «­» и «¯», то, используя закон де Моргана (см. табл. 3.5), сможем представить их следующим образом:

х₁ ­ х₂ = = +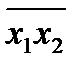

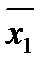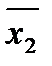
х₁ ¯ х₂ = = ×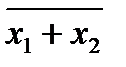

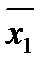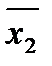
Вентили И-НЕ и ИЛИ-НЕ могут использоваться и с более чем двумя входными переменными, и действуют они в соответствии с очевидным обобщением закона де Моргана:

х₁ ­ х₂­…­x_n = = + +…+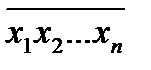

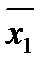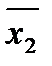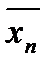
и

х₁ ¯ х₂ ¯…¯ x_n = = × …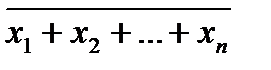

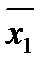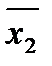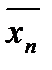
Разработка логических схем с вентилями И-НЕ и ИЛИ-НЕ не так проста, как разработка схем с вентилями И, ИЛИ и НЕ. Одной из главных трудностей в решении этой задачи является то, что по отношению к операциям И-НЕ и ИЛИ-НЕ ассоциативный закон не действует. Позже мы с вами еще вернемся к этой проблеме. Но сейчас давайте рассмотрим простую и универсальную процедуру синтеза произвольной логической функции с использованием только вентилей И-НЕ. Эту процедуру легче всего продемонстрировать на примере. Произведем алгебраическое преобразование логического выражения, соответствующего схеме с четырьмя входными переменными, которая включает три вентиля И-НЕ, имеющих по две входные переменные:

(х₁ ­ х₂) ­ (х₃ ­ x₄) = 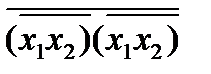= = 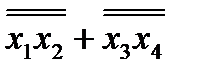х₁х₂ + х₃x₄

Для выполнения нужных преобразований мы воспользовались законами де Моргана и возведения в степень. На рис. А.8 показаны логические схемы, соответствующие этим преобразованиям. Поскольку любую логическую функцию окно синтезировать с помощью суммы произведений (И-ИЛИ) и поскольку и веденные преобразования обратимы, мы можем сделать вывод, что любую логическую функцию можно синтезировать в форме И-НЕ-И-НЕ.

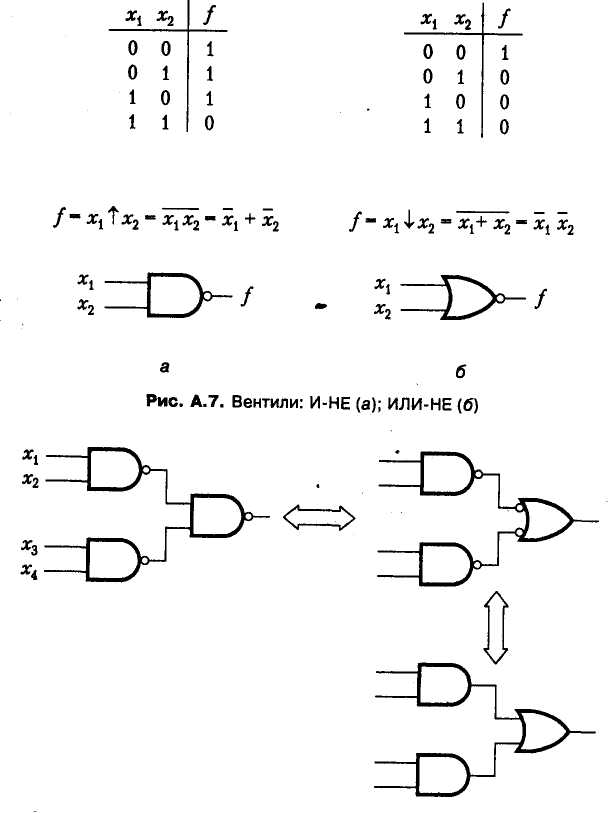
Рис. 3.16. Эквивалентные схемы на основе вентилей И-НЕ и вентилей И и ИЛИ

Причем это предположение верно для функций с любым количеством переменных. Очевидно, что общее количество входных переменных вентилей И-НЕ при этом должно быть таким же, как общее количество входных переменных вентилей И и ИЛИ.

Теперь давайте вернемся к вопросу о затруднении, возникающем вследствие того, что оператор И-НЕ не подчиняется ассоциативному закону. При разработке логической схемы на основе вентилей И-НЕ с использованием процедуры, иллюстрируемой рис. 3.16, может потребоваться вентиль И-НЕ с большим количеством входов, чем можно реализовать физически. Для схемы на основе вентилей И и ИЛИ это не проблема, поскольку благодаря ассоциативности данных операций один вентиль с большим количеством входов можно заменить несколькими вентилями с меньшим количеством входов, как на рис. 3.17, а. В случае вентиля И-HE решение не так просто. Например, функцию И-НЕ с тремя входными переменными нельзя реализовать в виде соединения двух вентилей И-НЕ, имеющих по два входа. Как показано на рис. 3.17, б, для ее реализации потребуется три вентиля И-НЕ.

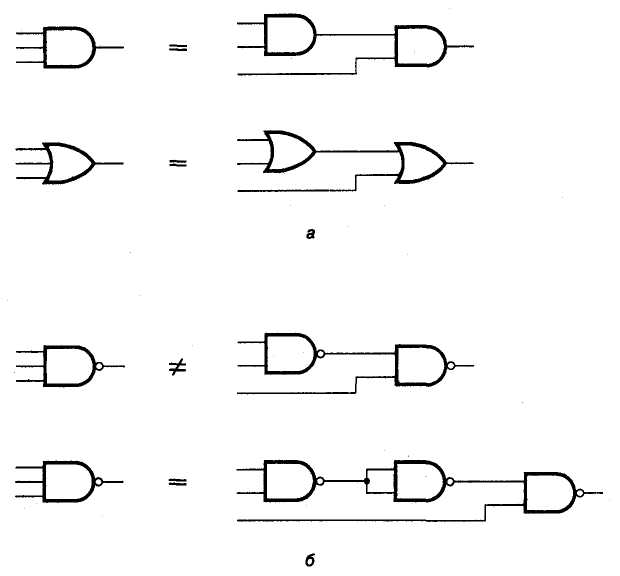
Рис. 3.17. Реализация логических функций с тремя входными переменными на основе вентилей с двумя входами: И и ИЛИ (а); И-НЕ (б)

Аналогичным образом строятся схемы на основе вентилей ИЛИ-НЕ: любая логическая функция может быть представлена в виде суммы произведений и реализована в виде эквивалентной схемы на основе вентилей ИЛИ-НЕ.

Лекция 16