Комбинации логических элементов
Цифровые системы строятся на основе комбинаций логических элементов. Такие комбинации могут быть описаны таблицей истинности, булевой функцией или логической схемой.
Рассмотрим таблицу истинности (табл. 3.3). Эта таблица описывает все возможные комбинации четырех входов (А, В, С, D). Заметим, что только комбинация 1010 даст 1 или Н-сигнал на выходе. Эквивалентная этой таблице истинности булева функция приведена в заголовке табл. 3.3. Входы подчинены операции И, что дает булеву функцию 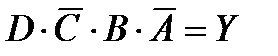 (читается как D и НЕ-С и В и НЕ -A дают на выходе Y).
(читается как D и НЕ-С и В и НЕ -A дают на выходе Y).
Таблица 3.3. получение булевой функции из таблицы истинности 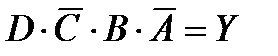
| Входы | Выход | Входы | Выход |
| D С В А | Y | D С В А | Y |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 | 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
Логическая схема построена исходя из булевой функции (см. рис. 3.8, а). Входы А и С должны быть инвертированы инверторами. На выходе использован элемент И с четырьмя входами.
Явно более простой вариант такой логической схемы приведен на рис. 3.8, б. На этой схеме инверторы 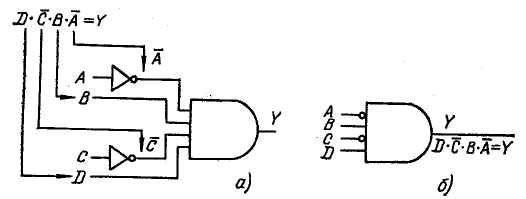
Рис. 3.8. Построение логических схем:
а — на основании булевой функции; б — упрощенный вариант
обозначены маленькими кружками, называемыми кружками инверсии, которые могут рассматриваться как LOW- активные входы. Другими словами, чтобы активизировать элемент И, на рис. 3.8, б входы А к С должны быть LOW, a входы В и D — HIGH. Так как входы D и В должны быть HIGH для активизации элемента И, их называют HIGH-активными входами.
Рассмотрим другую таблицу истинности (табл. 3.3). Здесь две комбинации входов вызовут 1 или HIGH на выходе. Булевой функцией, соответствующей этой таблице истинности, становится тогда такая: 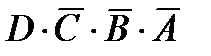 =
= 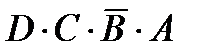 = Y (читается: D и НЕ-С и НЕ-В и НЕ-А или D и С и НЕ-В и А равно Y на выходе).
= Y (читается: D и НЕ-С и НЕ-В и НЕ-А или D и С и НЕ-В и А равно Y на выходе).
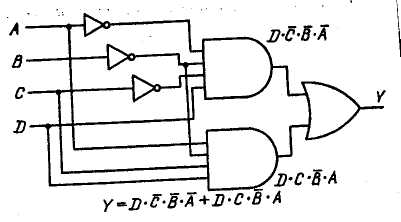
Рис. 3.9. Построение логической схемы по булевой функции
Затем на основании булевой функции получаем логическую схему (см. рис. 3.9). Заметим, что такая булева функция обусловлена сетью логических элементов И-ИЛИ, ближайшим к выходу является элемент ИЛИ. Такая специальная схема называется формой суммы произведений или реализованной формой булевой функции. Таблица 3.4 показывает состояние составляющих реализуемой булевой функции в колонке вывода таблицы истинности, где на выходе появляется 1.
Таблица 3.4. таблица истинности, соответствующая эквивалентному выражению 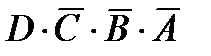 =
= 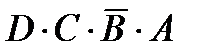 = Y
= Y
| Входы | Выход | Входы | Выход |
| D С В А | Y | D С В А | Y |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 | 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
Рассмотрим схему, которая состоит из двух вентилей И и одного вентиля ИЛИ (рис. 3.10. а). Она может быть представлена выражением
f =  •х2 + х1•
•х2 + х1• 
Схема составления таблицы истинности для этого выражения показана на рис. 3.10, б. Сначала для каждого входного значения определяются значения термов И, затем, с помощью операции ИЛИ, — результирующие значения функции f./ Таблица истинности функции f идентична таблице истинности функции Исключающее ИЛИ, так что схема с тремя вентилями, показанная на рис. 3.10, а, реализует функцию Исключающее ИЛИ с помощью вентилей И, ИЛИ и НЕ.
Логическое выражение  •х2 + х1•
•х2 + х1•  называется суммой произведений, поскольку операцию ИЛИ иногда называют суммой, а операцию И — произведением. Следует отметить, что правильнее было бы записать это выражение так: f = ((
называется суммой произведений, поскольку операцию ИЛИ иногда называют суммой, а операцию И — произведением. Следует отметить, что правильнее было бы записать это выражение так: f = ((  •х2) + (х1•(
•х2) + (х1•(  ))
))
Такая форма записи, как вы понимаете, отражает порядок применения логических операций. Для упрощения подобных выражений определяют иерархию операций И, ИЛИ и НЕ. Если в выражении отсутствуют скобки, логические операции выполняются в следующем порядке: сначала НЕ, затем И и только после этого ИЛИ. Более того, оператор «•» часто вовсе пропускают, если выражение не допускает двухзначной интерпретации.
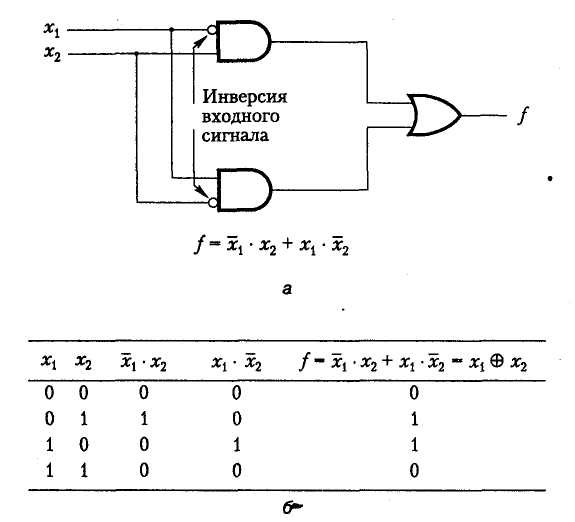
Рис. 3.10. Реализация функции Исключающее ИЛИ с использованием вентилей И, ИЛИ и НЕ: схема для функции Исключающее ИЛИ (а); таблица истинности для выражения  •х2 + х1•
•х2 + х1•  (б)
(б)
Возвращаясь к сумме произведений, мы сейчас покажем, как можно синтезировать любую логическую функцию непосредственно на основе ее таблицы истинности (табл. 3.5).
табл. 3.5. функции трех переменных
| х1 | х2 | х3 | f1 | f2 |
Предположим, мы хотим составить схему функции f1 на основе вентилей И, ИЛИ и НЕ. Для каждой строки таблицы, в которой f1 = 1, в формулу суммы произведений включается терм И со всеми тремя входными переменными. К одной, двум или трем из этих переменных по отдельности нужно применить оператор — НЕ таким образом, чтобы терм был равен 1 только в том случае, когда значения переменных соответствуют данной строке таблицы истинности. Это означает, что если в этой строке хi = 0, в произведение включается элемент 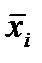 , а если хi = 1 -элемент хi. Например, в четвертой строке таблицы истинности значение функции 1 соответствует входным значениям
, а если хi = 1 -элемент хi. Например, в четвертой строке таблицы истинности значение функции 1 соответствует входным значениям
(x1 х2 х3) - (0, 1, 1)
Данной строке соответствует терм  х2х3. Составив аналогичные термы для всех строк таблицы истинности, в которых функция f1 имеет значение 1, мы получим вот такую сумму произведений:
х2х3. Составив аналогичные термы для всех строк таблицы истинности, в которых функция f1 имеет значение 1, мы получим вот такую сумму произведений:
f1 = 

 +
+ 
 х3 +
х3 +  х2х3 + x1х2х3
х2х3 + x1х2х3
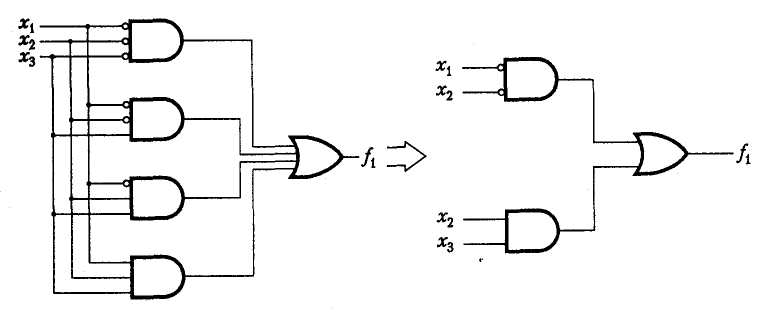
Логическая схема, соответствующая этому выражению, приведена в левой части рис. А.4. В качестве еще одного примера использования описанного алгоритма можно сформировать сумму произведений для функции Исключающее ИЛИ. Этот алгоритм может применяться с целью формирования суммы произведений и соответствующей логической схемы на основе таблицы истинности любого размера.
f1 = 

 +
+ 
 х3 +
х3 +  х2х3 + x1х2х3f1 =
х2х3 + x1х2х3f1 = 
 + х2х3
+ х2х3
Рис. 3.11. Логическая схема для функции f1 и соответствующая ей минимальная схема реализации
Упражнения
3.10. Записать выражение булевой функции таблицы истинности (табл.3.6.).
3.11. Начертить логическую схему системы, соответствующую таблице истинности (табл. 3.6).
3.12. Обратимся к рис. 3.12, б. Входы А. В и С _ (H-L) активные, тогда как вход D _____ (Н-, L-) активный.
Таблица 3.6. Таблица истинности.
| Входы | Выход | Входы | Выход |
| D С В А | У | D C В А | Y |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 | 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
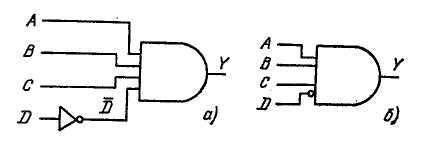
Рис. 3.12. Логическая схема (а) и ее упрощенный вариант (б)
3.13. Записать выражение булевой функции таблицы истинности (табл. 3.7).
Таблица 3.7. таблица истинности.
| Входы | Выход | Входы | Выход |
| D С В А | У | D C В А | Y |
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 | 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
3.14. Начертить логическую схему системы, соответствующую таблице истинности (табл. 3.7).
Решения
3.10. Единицу на выходе дает единственное сочетание входов. Выражение булевой функции получается в виде 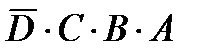 = Y 3.11. Выражением реализуемой функции для табл. 3.6 будет
= Y 3.11. Выражением реализуемой функции для табл. 3.6 будет 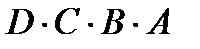 = Y. Его реализация осуществляется схемой, представленной на рис. 3.12, а. На рис. 3.12, б приведено другое возможное решение. 3.12. На рис. 3.12, б входы А, В и С являются Н-активными, а вход D—L-активный. Действительно, элемент И с четырьмя входами может быть активизирован (1 на выходе) только тогда, когда входы А, В к С будут Н-активными, а вход D—L-активный. 3.13. Н-уровень на выходе получается при двух сочетаниях входов согласно таблиц истинности (табл. 3.7). Для этих двух случаев и получено выражение булевой функции
= Y. Его реализация осуществляется схемой, представленной на рис. 3.12, а. На рис. 3.12, б приведено другое возможное решение. 3.12. На рис. 3.12, б входы А, В и С являются Н-активными, а вход D—L-активный. Действительно, элемент И с четырьмя входами может быть активизирован (1 на выходе) только тогда, когда входы А, В к С будут Н-активными, а вход D—L-активный. 3.13. Н-уровень на выходе получается при двух сочетаниях входов согласно таблиц истинности (табл. 3.7). Для этих двух случаев и получено выражение булевой функции 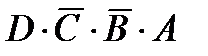 +
+ 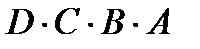 = Y.
= Y.
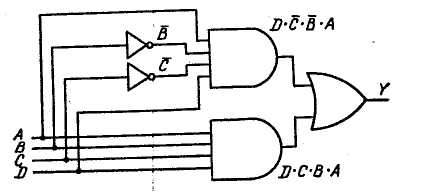
Рис. 3.13. Логическая схема, соответствующая табл. 3.7
3.14. Выражением булевой функции для этой таблицы истинности будет 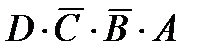 +
+ 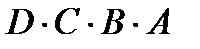 = Y, на основании которого строим логическую схему рис. 3.13.
= Y, на основании которого строим логическую схему рис. 3.13.
Дата добавления: 2016-07-05; просмотров: 4056;











