Минимизация функций с использованием карты Карно

При минимизации функций f₁ и f₂ из табл. 3.2 нам приходилось искать наиболее активные способы преобразования исходных выражений. Например, далеко не очевидным было решение повторить терм на первом шаге минимизации функции f_2.- Для того чтобы как можно быстрее получить минимальное выражение, представляющее логическую функцию нескольких переменных, можно воспользоваться графическим представлением таблицы истинности, называемым картой Карно. Для функции трех переменных карта Карно представляет собой прямоугольник, составленный из восьми квадратов, расположенных в два ряда по четыре в каждом (рис. 3.14, а). Каждый квадрат соответствует конкретному набору значений входных переменных. Например, третий квадрат в верхнем ряду представляет значения (x₁ х₂, х₃) = (1, 1, 0).

Поскольку в таблице истинности функции трех переменных содержится восемь строк, карта должна состоять из восьми квадратов. Значения внутри квадратов — это значения функции при соответствующих значениях переменных.

Главная идея карты Карно заключается в том, что расположенные рядом по горизонтали и по вертикали квадраты отличаются значениями только одной переменной. Если два смежных квадрата содержат единицы, это означает возможность алгебраического упрощения соответствующей пары термов. Например, на карте функции f₂ (рис. 3.14, а) единицы в двух крайних слева квадратах верхнего ряда соответствуют термам и х₂ . Эта пара термов упрощается следующим образом:

+ х₂ .= .

что мы и сделали в предыдущем разделе при минимизации алгебраического выражения для функции f₂. Минимизированное произведение, соответствующее группе квадратов, — это произведение входных переменных, значения которых одинаковы для всех квадратов этой группы. Если значение входной переменной х_i равно нулю для всех квадратов группы, тогда переменная х_i входит в результирующее произведение. Квадраты с левого края карты считаются смежными с квадратами с ее правого края. Так, в карте функции f₂ имеется группа из четырех единиц, состоящая из крайнего слева столбца и крайнего справа столбца карты, Соответствующая группа термов упрощается до одного терма , содержащего единственную переменную, поскольку только переменная х₂ имеет одинаковые значения во всех квадратах группы.

Рис. 3.14. Минимизация функций с использованием карт Карно: карта для трех переменных (а); карта для четырех переменных (б);

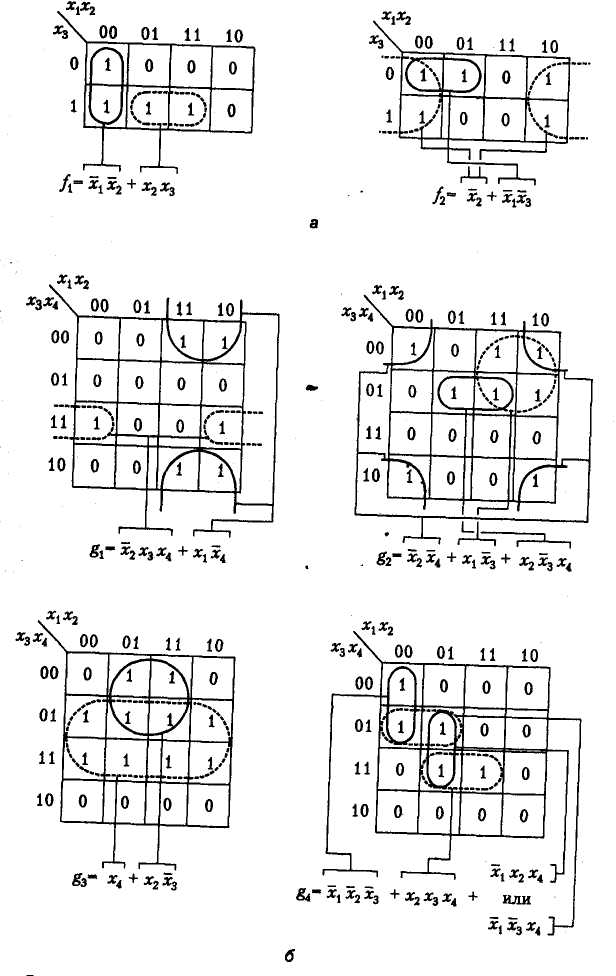
Карты Карно могут использоваться и для минимизации функций более чем трех переменных. Карту для четырех переменных можно составить из двух карт для трех переменных. Два примера таких карт показаны на рис. 3.14, б, и под каждой из них приведено минимальное выражение для представляемой ею функции Если на карте для трех переменных квадраты можно группировать по два и по четыре, то на карте для четырех переменных их можно группировать еще и по восемь. Пример такой группировки показан на карте функции g₃ Обратите внимание, что четыре угловых квадрата можно объединить в одну группу, как на карте функции g₂, где на их основе составлен терм 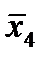. Как и в случае карты для трех переменных, терм, соответствующий группе квадратов, представляет собой произведение переменных, значения которых одинаковы для всех квадратов этой группы. Так, в группе из четырех квадратов в правом верхнем углу карты функции g₂ во всех квадратах х₁ = 1 и х₃ = 0, поэтому эту группу представляет терм х1 . Остальные две переменные, х₂ и x₄ имеют в квадратах этой группы разные значения. Карты Карно можно использовать и для функций пяти переменных. В этом случае для представления функции используются две карты для четырех переменных: одна из них соответствует значению 0 пятой переменной, а другая – ее значению 1.

Общая процедура формирования на карте Карно групп из двух, четырех, восьми и т. д. квадратов определяется просто. Две смежные пары квадратов, содержащих единицы, можно объединить в группу из четырех квадратов. Две смежные группы по четыре квадрата можно объединить в группу из восьми квадратов.

В общем случае количество квадратов в группе должно быть равным 2^k, где k — целое число.

Теперь давайте рассмотрим процедуру получения с помощью карты Карно минимальной суммы произведений. Как видно на рис. 3.14, большей группе квадратов соответствует произведение меньшего числа переменных. Поэтому для получения минимального выражения нужно объединить все квадраты на карте, содержащие единицы, в как можно меньшее количество групп, выбирая наибольшие из них, так чтобы при этом охватить все единицы. Для примера рассмотрим карту функции g2 приведенную на рис. 3.14, б.

Как вы уже знаете, единицы по ее углам составляют группу из четырех квадратов, представляемую термом 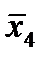. Еще одна группа из четырех квадратов располагается в правом верхнем углу и представлена термом х₁ . Эти две группы охватывают все единицы на карте, за исключением одной единицы в квадрате (х₁, х₂, х₃, х₄) = (0,1,0,1). Наибольшая группа единиц, включающая этот квадрат, — это группа из двух квадратов, представленная термом х₂ х₄. Таким образом, минимальное выражение для функции g₂ должно быть следующим:

g₂ = 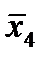+ х₁ + х₂ х₄

Минимальные выражения для других функций, представленных на рис. 3.14, б, формируются аналогичным образом. Обратите внимание, что в случае функции g₄ существует два альтернативных выражения: одно включает терм х₂х₄ а второе — терм х₄.Такое случается довольно часто.

Во всех наших примерах составить минимальное выражение достаточно просто. Вообще-то для этой цели существуют формальные алгоритмы, но мы их рассматривать не будем.