Электронные логические вентили

Наш пример с выключателями, замкнутыми и разомкнутыми электрическими цепями и лампочками, иллюстрирующий идею логических переменных и функций, удобен тем, что он очень прост и каждому знаком. При этом представленные логические концепции применимы к электрическим цепям, используемым в обработки информации в цифровых компьютерах.

Физическими переменными в данном случае являются не положения выключателей и замкнутые или разомкнутые цепи, а электрическое напряжение и ток. Для примера рассмотрим схему, предназначенную для работы со входным напряжением +5 В или 0 В. Возможные значения выходного напряжения в ней тоже составляют +5 или 0 В. Если мы договоримся, что значение +5 В представляет логическую единицу, а знание 0 В — логический нуль, тогда функционирование этой схемы можно будет описать с помощью таблицы истинности той логической операции, которую она реализует.

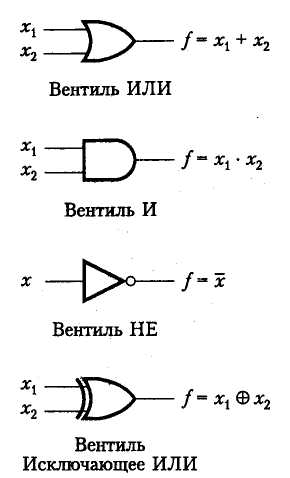
С применением транзисторов можно сконструировать простые электронные схемы, которые будут выполнять логические операции И, ИЛИ, Исключающее ИЛИ и НЕ. Эти базовые схемы традиционно называют вентилями (gates).

Стандартные обозначения вентилей всех четырех типов приведены на рис. 3.2. Если операция НЕ применяется ко входному или выходному значению логического вентиля, для нее используется упрощенное обозначение — просто маленький кружок.

Пока мы с вами поговорим о том, как с помощью базовых вентилей конструируются логические схемы, реализующие более сложные логические функции.

Рис. 3.2. Стандартные обозначения логических вентилей.

В табл. 3.2 приведены семь основных логических элементов цифровых систем. В таблице истинности 0 означает низкий уровень напряжения (LOW), a 1 — высокий (HIGH).

В правой колонке приведены булевы функции (Дж. Буль (1815-1864)—английский математик и логик, им заложены основы математической логики), выполняемые каждым из логических элементов.

Таблица 3.2.

Логические функции	Обозначения логических элементов	Таблицы истинности	Булева функция
Инвертор НЕ (NOT)		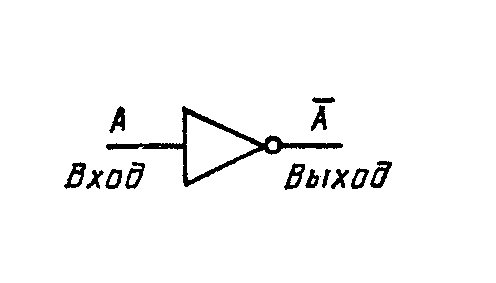Вход Выход А 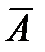0 1 1 0	А=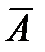
И (AND)   НЕ-И (NAND)		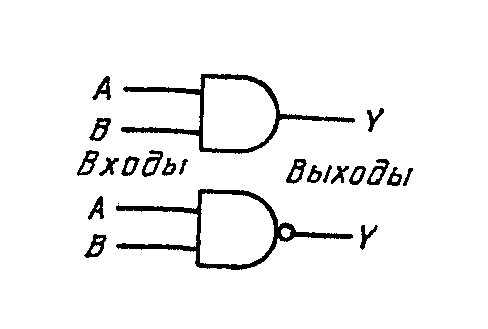Входы Выходы А В И НЕ-И 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0	A×B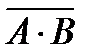=Y     =Y

Логические функции	Обозначения логических элементов	Таблицы истинности	Булева функция
ИЛИ (OR)     НЕ-ИЛИ (NOR)		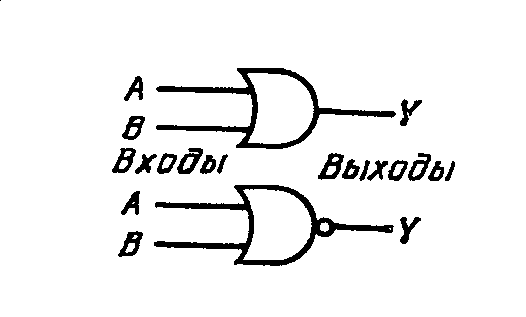Входы Выходы В А ИЛИ НЕ-ИЛИ 0 0 0 1 0 1 1 0 1 0 1 .0 1 1 1 0	A+B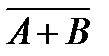=Y     =Y
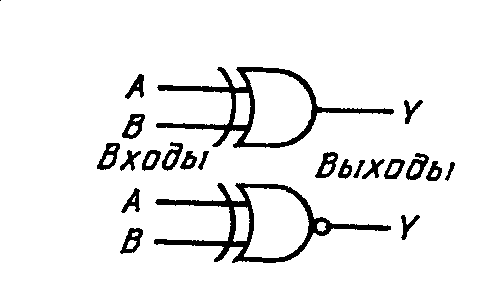
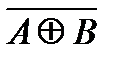ИЛИ ИСКЛЮЧАЮЩЕЕ (XOR)     НЕ-ИЛИ ИСКЛЮЧАЮЩЕЕ (XNOT-OR)		Входы Выходы В A XOR HE-XOR 0 0 0 1 0 1 1 0 1 0 1 0 1 1 0 1	A B=Y     =Y

Приведенный на рис. 3.3 пример несколько поясняет способ преобразования информации логическими элементами.

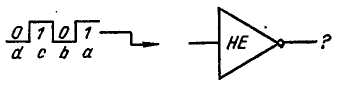
рис. 3.3 Пример инверсии

Каким будет сигнал на выходе инвертора (часто называется элементом отрицания НЕ) на рис. 3.3, когда на его вход поступает импульс а? Согласно второй строке таблицы истинности (табл. 3.2) на выходе должен быть 0, т.е. значение, противоположное входному сигналу. Когда на вход инвертора подается импульс b (О или LOW), выход перейдет в состояние 1 (Н-состояние). Импульс с вызовет LOW (L-состояние) на выходе, тогда как импульс d вызовет на выходе Н-состояние. Процесс инверсии называется также дополнением или отрицанием.

Булевой функцией дополнения является А= 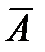(говорят НЕ— А). Черта сверху А читается как НЕ и означает, что надо инвертировать или дополнить (до 1) переменную, над которой она стоит.

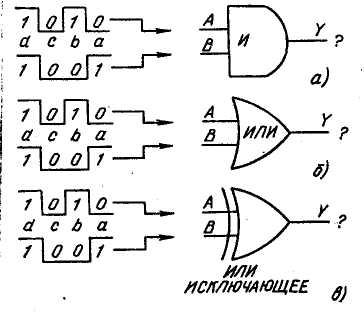
На рис. 3.4, а приведен другой пример — элемент И с двумя входами. Импульсами а на его входах являются 0 и 1. Согласно таблице истинности (табл. 3.2) это должно; вызвать 0 (LOW) на выходе. Импульсы а, б и с вызовут на выходе L-уровень. Когда же оба входа элемента И станут HIGH (см. импульсы d на рис. 3.4,а), выход становится равным 1 или HJGH.

Рассмотрим задачу, приведенную на рис. 3.4, б. В этом случае тетрады 1010 (на входе А) и 1001 (на входе В) совместно поступают на вход логического элемента ИЛИ. Тетрада на выходе может быть определена по таблице истинности (табл.3.2).

В результате логической операции ИЛИ над 1010 и 1001 получим на выходе 1011. Отметим, что функция ИЛИ сначала выполняется с импульсами а, затем б и т. д.

Рис. 3.4. Выполнение логических операций: а - И; б - ИЛИ; в - ИЛИ ИСКЛЮЧАЮЩЕЕ.

Какой будет тетрада на выходе, если 1010 и 1001 будут подвергнуты операции ИЛИ ИСКЛЮЧАЮЩЕЕ (XOR), как показано на рис. 3.4, в? Согласно таблице истинности XOR видим, что результатом операции XOR с тетрадами 1010 и 1001 будет 0011.

Таким образом, микропроцессор может выполнять логические операции. Обычно микропроцессоры наделены способностью выполнять команды логических операций НЕ (дополнение или отрицание), И, ИЛИ и ИЛИ ИСКЛЮЧАЮЩЕЕ. Эти команды выполняются побитно аналогично приведенным в табл. 3.2 и на рис. 3.3, 3.4.

Упражнения

3.1. Перечислить семь логических функций.

3.2. Перечислить четыре логические функции, которые могут быть выполнены, как правило, одной командой.

3.3. Если МП выполняет функцию 1100 И 1011, тетрадой выхода будет ____.

3.4. Если МП выполняет функцию 0011 ИЛИ 1000, тетрадой выхода будет ___.

3.5. Если МП инвертирует (операция НЕ) тетраду1001, результатом будет ___.

3.6. Если МП выполняет функцию 0011 ИЛИ ИСКЛЮЧАЮЩЕЕ 0110, результатом будет ____.

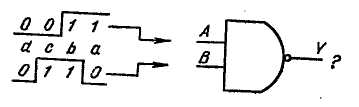
Записать выходы элемента НЕ-И на рис. 3.5

Рис. 3.5. К упражнению 3.7

3.7. Записать выходы элемента НЕ-ИЛИ на рис. 3.6.

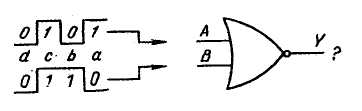Рис. 3.6. К упражнению 3.7

3.8. Записать выходы элемента НЕ-ИЛИ ИСКЛЮЧАЮЩЕЕ на рис. 3.7.

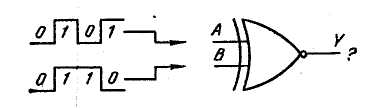Рис. 3.7. К упражнению 3.8

Решения

3.1. См. табл. 3.2. Семь логических функций: НЕ (инверсия), И, НЕ-И, ИЛИ, НЕ-ИЛИ, ИЛИ ИСКЛЮЧАЮЩЕЕ, НЕ-ИЛИ ИСКЛЮЧАЮЩЕЕ. 3.2. НЕ, И, ИЛИ и ИЛИ ИСКЛЮЧАЮЩЕЕ. 3.3. См. табл.3.2. Результат 1000. 3.4. См. табл. 3.2— таблица истинности ИЛИ. 1011. 3.5. 0110. 3.6.0101. 3.7. См. таблицу истинности в табл. 3.2. Импульсы на выходе будут иметь значения: при импульсах а—1; при импульсах б — 0; при импульсах с—1; при импульсах d—1; 3.7. При импульсах а— 0; при импульсах b — 0; при импульсах с — 0; при импульсах d— 1. 3.8. При импульсах а—0; при импульсах b — 0; при импульсах с— 1;при импульсах d — 1.

Лекция 10