Логические элементы

В цифровых компьютерах информация представляется и обрабатывается с помощью электронных логических схем. Логические схемы оперируют двоичными переменными, принимающими одно из двух значений (обычно таковыми являются нуль и единица).

Используемые для обработки цифровых сигналов устройства называются логическими элементами, и для их идентификации используют логические символы.

Рассказ о двоичной логике проще всего начать с простого примера, знакомого многим из вас. Представьте себе обычную электрическую лампочку, состояние которой (включена/выключена) управляется двумя выключателями, х₁ и х₂. Каждый из выключателей может находиться в одном из двух возможных положений, 0 или 1 (рис. 3.1, а).

Это означает, что его можно представить как двоичную переменную. Поэтому пусть имена переключателей служат и именами соответствующих им двоичных переменных. Еще на рисунке показаны источник питания и сама лампочка. То, как выключатели будут управлять включением и выключением лампочки, зависит от соединения их проводов. Свет горит лишь в том случае, если образуется замкнутый контур, соединяющий лампочку с источником питания. Пусть условие включения лампочки представляет двоичная переменная f.

Если лампочка включена, значит, f = 1, а если она выключена, то f = 0. Таким образом, условие f = 1 указывает, что в цепи существует как минимум один замкнутый контур, а условие f = 0 означает, что замкнутого контура нет. Очевидно, что f является функцией двух переменных, х₁ и х₂.

Теперь давайте рассмотрим существующие способы управления лампочкой. Для начала, предположим, что она будет гореть при условии, что хотя бы один из переключателей находится в положении 1, то есть f = 1, если

х₁ = 1 и х₂ = 0

или

х₁ = 0 и х₂ = 1

или

х₁ = 1 и х₂ = 1

Соединения, реализующие этот тип управления, показаны на рис. 3.1,б. Рядом со схемой приведена представляющая эту ситуацию логическая таблица истинности. В таблице перечислены все возможные пары установок переключателей и соответствующие им значения функции f. В терминах математической логики эта таблица представляет функцию ИЛИ (OR) переменных х₁ и х₂.

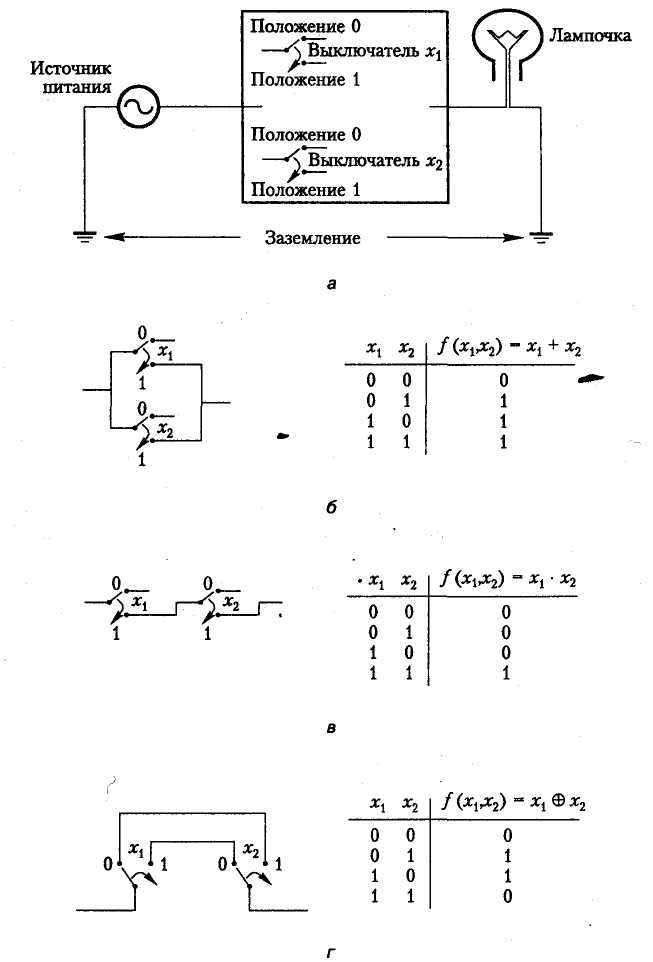
Рис. 3.1. Схемы включения электрической лампочки: лампочка, управляемая двумя выключателями (а); параллельное соединение выключателей — схема ИЛИ (б); последовательное соединение выключателей — схема И (в); соединение выключателей по схеме Исключающее ИЛИ (г)

Операцию ИЛИ обычно представляют алгебраическим знаком <+» или «Ú» так что

f = х₁ + х₂ = х₁ Ú х₂

Мы говорим, что х₁ и х₂ являются входными переменными, а f — это выходная функция.

Следует указать некоторые важнейшие свойства операции ИЛИ. Прежде всего, она коммутативна, то есть

х₁ + х₂ = х₂ + х₁

Данная операция может распространятся на n переменных, так что функция

f = х₁ + х₂ + ...+ x_n

принимает значение 1, если это же значение имеет хотя бы одна переменная x_n . Проанализировав таблицу истинности, вы увидите, что

1 + х = 1

и

0 + х = х

А теперь предположим, что лампочка должна загораться только в том случае, если оба выключателя находятся в положении 1. Такая схема соединения выключателей с соответствующей ей таблицей истинности показана на рис. 3.1, в. Эта схема соответствует функции И (AND), для обозначения которой используется символ <•> или «Ù»:

f = х₁•х₂ = х₁ Ù х₂

Вот важнейшие свойства операции И:

х₁•х₂ = х₂• х₁

1•х = х

0•х = 0

Функцию И тоже можно распространить на n переменных:

f = х₁•х₂ • ... • х_n

Эта функция имеет значение 1 только в том случае, если все переменные х имеют значение 1. Она представляет такую же схему, как на рис. 3.1, в, в которой правда, последовательно соединено большее количество выключателей.

Последний вариант соединения выключателей также достаточно распространен. Здесь выключатели подсоединены с двух концов ступенчатого контура, так что лампочку можно включать и выключать с помощью любого из них. Это означает, что если свет включен, изменением положения любого из выключателей его можно выключить, а если свет выключен, изменением положения любого из выключателей его можно включить.

Предположим, что лампочка не горит, когда оба выключателя находятся в положении 0. Переключение же любого из них в положение 1 включает лампочку. Теперь предположим, что лампочка горит, если х₁ = 1, х₂ = 0. Переключение х₁ в положение 0 выключает лампочку. Более того, для ее выключения можно также установить х₂ в положение 1, то есть f = 0, если x₁ = х₂ =1. Соединение, которое реализует этот способ управления лампочкой, показано на рис. 3.1, г. Соответствующая логическая операция, представляемая символом «Å», называется Исключающее ИЛИ (EXCLUSIVE-OR или XOR). Приведем ее важнейшие свойства:

x₁ Å х₂ = х₂ Å x₁

1 Å х =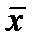

0 Å х = х

где 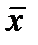обозначает функцию НЕ (NOT) от переменной х. Эта функция переменной f = 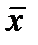имеет значение 1, если х = 0, и значение 0, если х = 1. В подобном случае мы говорим, что входное значение х инвертируется или дополняется.