Шестнадцатеричные числа
Двоичные числа
Вычислительные машины работают с двоичными числами. Двоичная система счисления или система с основанием 2 использует только цифры 0 и 1. Эти двоичные числа названы битами (от binary digit). Физически в цифровых электронных системах бит 0 представлен напряжением LOW (низким), а бит 1—напряжением HIGH (высоким).
Человеческая деятельность предполагает использование десятичной системы счисления. Десятичная система, или система с основанием 10, содержит 10 цифр (от 0 до 9). Она также характеризуется значением позиции (или весом). В табл. 2.1 показано, например, что десятичное число 1327 равно одной тысяче, плюс три сотни, плюс два десятка, плюс семь единиц (1000+300+20+7=1327).
Двоичная система обладает также свойством уравновешивания.
Таблица 2.1. Значения позиций десятичных чисел
| Степень основания | 103 102 101 100 |
| Значения позиций | 1000 100 10 1 |
| Десятичные | 1 3 2 7 1000 + 300 + 20 + 7=1327 |
В табл. 2.2 приведены десятичные значения первых четырех двоичных позиций. Двоичное число 1001 (произносится: один, нуль, нуль, один) преобразовано, таким образом, в свой десятичный эквивалент 9. Бит единицы двоичного числа в табл. 2.2 называется младшим битом (МБ), бит восьмерки— старшим битом (СБ).
Таблица 2.2. Значения позиций двоичных чисел
| Степень основания i | 23 22 21 20 |
| Значения позиций | 8 4 2 1 |
| Двоичное Десятичное | СБ. МБ 1 0 0 1 8 + 0 + 0 + 1=9 |
В табл. 2.3 приведены десятичные числа от 0 до 15, а также их двоичные эквиваленты. Те, кто работает в области использования ЭВМ, должны, по меньшей мере, запомнить эти двоичные числа.
Таблица 2.3. Десятичные числа и их двоичные эквиваленты
| десятичные | двоичные |
| 10 1 | 8 4 2 1 |
| 1 0 1 1 1 2 1 3 1 4 1 5 | 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
Как преобразовать двоичное число 1011 0110 (т.е. один, нуль, один, один, нуль, один, один, нуль) в его десятичный эквивалент? Процедура преобразования выполняется в соответствии с табл. 2.4. Десятичные значения каждой позиции записаны под каждым битом, затем десятичные числа суммируются (128+32+16+4+2=182), что дает 182.
Таблица 2.4. Двоично-десятичные преобразования
| Степень основания | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | ||
| Значение позиций | ||||||||||
| Двоичное Десятичное | + | + | + | + | 0 = 182 |
Обычно основание системы счисления указывается индексами. Таким образом, число 1011 01102 является двоичным (или основания 2), а число 18210 — десятичным: 1011 01102 = 18210. Как преобразовать десятичное 155 в его двоичный эквивалент? Процедура преобразования приведена на рис.2.1.
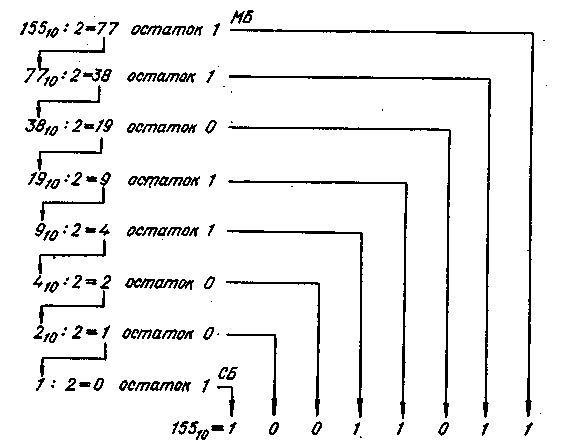
Рис. 2.1. Двоично-десятичные преобразования
Десятичное 155 сначала делится на 2, что дает нам частное 77 и остаток 1. Этот остаток становится МБ двоичного числа и помещается в эту позицию (см. рис. 2.1). Затем частное (77) перемещается, как показывает стрелка, и становится следующим делимым. Затем каждое частное последовательно делится на 2 до тех пор, пока не получится частное, равное 0, и остаток, равный 1 (см. предпоследнюю строку на рис. 2.1). Последняя строка на рис. 2.1 дает нам результат 15510=1001 10112.
Упражнения
2.1.Большинство людей в своей практической деятельности использует десятичную систему, цифровая ЭВМ использует ______ систему.
2.2.В двоичной системе бит означает ___________ .
2.3.Число 10010 является __________ числом.
2.4.Записать двоичное число один, один, нуль, нуль в цифровой форме.
2.5.Что означает сокращение МБ?
2.6.Преобразовать в десятичный код следующие двоичные числа: а) 0001; б) 0101; в) 1000; г) 1011; д) 1111;
е) 0111.
2.7. Преобразовать в десятичный код следующие двоичные числа: а) 10000000; 6)00010000; в) 00110011; г) 0110 0100; д) 0001 1111; е) 1111 1111. 2.8. Преобразовать в двоичный код следующие десятичные числа: а) 23; б) 39; е) 55; г) 48.
2.9. 20410=__________ 2 2.10. 1110 11102 =_____ 10
Решения
2.1. Двоичную или основания 2. 2.2. Двоичную цифру (binary digit). 2.3. Десятичным (основания 10). 2.4. 11002. 2.5. Младший бит. 2.6. Обратимся к табл. 2.3: a) 00012=110; б) 01012=510; в) 1000s=810; г) 10112= = 1110; д) 11112=1510; е) 01112=710. 2.7. Следуем процедуре, приведенной в табл. 2.2: а) 1000 00002=12810; б) 0001 00002=1610; в) 0011 00112=5110; г) 0110 01002=10010; д) 0001 11112=3110; е) 1111 11112=25510.2.8. См. рис. 2.1:
а) 2310: 2= 11, остаток 1 (МБ) б) 3910:2=19, остаток 1 (МБ)
11:2= 5, остаток 1 19 : 2= 9, остаток 1;
5 :2= 2, остаток 1 9 :2= 4, остаток 1;
2 : 2= 1, остаток 0 4:2=2, остаток 0;
1 :2= 0, остаток 1 (СБ); 2 :2- 1, остаток 0;
1 :2= 0. остаток 1 (СБ);
в) 5510:2=27, остаток 1 (МБ) г) 4810: 2=24, остаток 0 (МБ);
27 :2=13, остаток 1; 24 :2 = 12, остаток 0;
13 :2= 6, остаток 1; 12. :.2= 6, остаток 0;
6 : 2= 3, остаток 0; 6 : 2= 3, остаток 0;
3 : 2= 1, остаток 1; 3 : 2= 1, остаток 1;
1:2= 0, остаток 1 (СБ); 1 : 2= 0, остаток 1 (СБ).
2.9. Обратиться к рис. 2.1: 20410 =1100 11002 2.10. Обратиться к табл. 2.2: 1110 11102=23810.
Лекция 4
Шестнадцатеричные числа
Ячейка памяти типичной микро-ЭВМ может содержать двоичное число 1001 1110. Такая длинная цепь нулей и единиц сложна для запоминания и неудобна для ввода с клавиатуры. Число 1001 1110 могло бы быть преобразовано в десятичное, что дало бы 158ю, но процесс преобразований занял бы много времени. Большая часть систем микроинформатики использует шестнадцатеричную форму записи, чтобы упростить запоминание и использование таких двоичных чисел, как 1001 1110.
Шестнадцатеричная система счисления (hexadecimal)', или система с основанием 16, использует 16 символов от 0 до 9 и А, В, С, D, Е, F. В табл. 2.5 приведены эквиваленты десятичных, двоичных, и шестнадцатеричных чисел.
Заметим из табл. 2.5, что каждый шестнадцатеричный символ может быть представлен единственным сочетанием четырех бит, Таким образом, представлением двоичного числа 1001 1110 в шестнадцатеричном коде является число 9Е. Это значит, что часть 1001 двоичного числа равна 9, а часть 1110 равна Е (конечно, в шестнадцатеричном коде). Следовательно, 1001 11102=9E16. (He следует забывать, что индексы означают основание системы счисления.)
-Как преобразовать двоичное число 111010 в шестнадцатеричное? Надо начать с МБ и разделить двоичное число на группы из 4 бит. Затем надо заменить каждую группу из 4 бит эквивалентной шестнадцатеричной цифрой: 10102=А, 00112=3, следовательно, 1110102= 3A16.
Как преобразовать шестнадцатеричное число 7F в двоичное? В этом случае каждая шестнадцатеричная цифра должна быть заменена своим двоичным эквивалентом из 4 бит.
Таблица 2.5. Десятичные, шестнадцатеричные и двоичные эквиваленты
| Десятичные | Шестнадцатеричные | Двоичные ые | |||
| А В С D E F |
В примередвоичное число 0111 заменено шестнадцатеричной цифрой 7, а 11112 заменяет F16, откуда 7F16= 1111 01112.
Шестнадцатеричная запись широко используется для представления двоичных чисел, поэтому необходимо табл.2,5 также запомнить.
Таблица 2.6. Преобразование шестнадцатеричного числа в десятичное
| Степень шестнадцати | 163 | 162 | 161 | 160 | ||||
| Значение позиции | ||||||||
| Шестнадцатеричное Десятичное | x | + | С 256 X | + | 6 16 X 6 | + | Е X - | =1137410 |
Преобразуем шестнадцатеричное число 2С6Е в десятичное. Процедура действий соответствует табл. 2.6. Значениями позиций первых четырех шестнадцатеричных цифр являются соответственно слева направо 4096, 256, 16 и 1. Десятичное число содержит 14 (Е]6) единиц, 6 чисел 16, 12 (C16) чисел 256 и 2 числа 4096. Каждая цифра умножается на соответствующий ей вес, получается сумма, которая и дает нам десятичное число 11374.
Преобразуем десятичное число 15797 в шестнадцатеричное. На рис. 2.2 показана процедура действий. В первой строке 1579710 разделено на 16, что дает частное 98710 и остаток 510, который преобразуется затем в свой шестнадцатеричный эквивалент (510=516) и становится цифрой младшего разряда (МР) шестнадцатеричного числа.
Первое частное (987) становится делимым во второй строке и снова делится на 16, что дает частное 61 и остаток 11 или шестнадцатеричное В. В третьей строке 61 делится на 16, дает частное 3 и остаток 1310 или D16, а в четвертой строке делимое 3 делится на 16, дает частное 0 и остаток 310 или 316. Когда частное равно 0, как в четвертой строке, преобразование заканчивается. 316 становится цифрой старшего разряда (СР) результата, т.е. 3DB516.
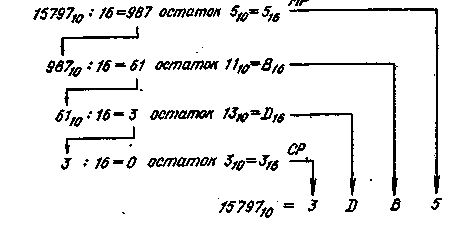
Рис. 2.2. Десятично-шестнадцатеричное преобразование
Упражнения
2.11. Шестнадцатеричная запись широко используется как сокращенная форма записи ____ (двоичных, десятичных) чисел.
2.12. Шестнадцатеричная система имеет основание____ .
2.13. Записать следующие шестнадцатеричные числа в двоичной форме: а) С; б) 6; в) F; г) Е; д) 1А; е) 3D; ж) АО; з) 8В; и) 45; к) D7.
2.14. Преобразовать следующие двоичные числа в шестнадцатеричный код: а) 1001; б) 1100; в) 1101; г) 1111; д) 1000 0000; е) 0111 1110; ж) 001 0101; з) 1101 1011.
2.15. Преобразовать следующие шестнадцатеричные числа в десятичный код: а) 7Е; б) DB; в) 12А3; г) 34CF.
2.16. 21710=__________ 16.
2.17.48373,0=__________ 16.
Решения
2.11.Двоичных 2.12.16. 2.13. Используя табл. 2.5 и процедуру, приведенную § 2.2, получаем: а) СН=11022; б) 6Н=01102; в) РН= 11112; г) Е2Н=1110 00102; д) 1АН=0001 10102; е) 3DH=0011 11012; ж) АОН=1010 0000;
з) 8ВН=1000 10112; и) 45Н=0100 01012; к) D7H=1101 01112.: 2.14. а) 11012=9Н; б) 11002=СН; в) 11012=DH; г) 11112=FH; д) 1000 00002=80Н; е) 0111 11102=7ЕН; ж) 001 01012=15Н; з) 1101 10112=DBH. 2.15. а) 7ЕН=(16*7) + (1*14) = 12610; б) DBH=(16*13) + (1 *14)=21910; в) 12A3H=(4096*1) + (256*2) + (16*10)+(1*3) = 4771010; г) 34CFH= (4096*3) -Н (256*4) + (16* 12) + (1*15) = 13519,0.
2.16.21710=D9H— действия следующие: 21710: 16=13, остаток 910=9Н (МР); 1310: 16= 0, остаток 1310=DH (CP).
2.17.4837310: 16=3023, остаток 510=5Н (МР); 3023 : 16= 188, остаток 1510=FH; 188:16= 11, остаток с 1210=СН; 11 : 16= 0, остаток 1 1110= ВН (СР). Таким образом, 4837310=BCF5H.
Дата добавления: 2016-07-05; просмотров: 5410;











