Дополнительный код. Арифметика в дополнительном коде

Сама ЭВМ обрабатывает информацию обычно в двоичном коде. Однако если нужно использовать числа со знаком, используется специальный дополнительный код, что упрощает аппаратные средства ЭВМ.

На рис. 2.6,а приведено обычное изображение регистра МП или ячейки памяти вне МП. Такой регистр представляют пространством из 8 бит данных.

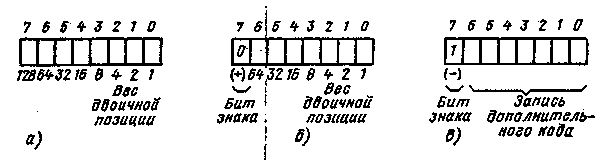
Рис. 2.6. Изображение регистра МП или ячейки памяти:

а — расположение двоичных позиций; б — идентификация положительных чисел нулем в знаковом бите; в — идентификация отрицательных чисел единицей в знаковом бите

Таблица 2.10. Десятичные числа со знаком и их представление в дополнительном коде

Позиции бит пронумерованы от 7 до 0, а веса двоичных позиций указаны в основании регистра, бит 7 имеет вес 128, бит 6 — 64 и т. д.

На рис. 2.6, б и в показаны типовые структуры 8-разрядных регистров для размещения чисел со знаком. В обоих случаях бит 7 является знаковым. Он указывает, является ли число положительным (+) или отрицательным (—). При 0 в знаковом бите число положительно, при 1 — отрицательно.

Если, как показано на рис. 2.6,б, число положительно, оставшиеся ячейки памяти (6-0) содержат двоичное 7-разрядное число. Например, если регистр на рис. 2.6,б содержит 0100 0001, это соответствует числу +65 ₁₀ (64+1, знаковый бит положителен). Если в него записано 0111 1111, содержимым будет +127₁₀ (знаковый бит положителен: 64+32+4+16+8+4-+2+1), что является наибольшим. Если, как это показано на рис. 2.6, в, регистр содержит то же число со знаком, но отрицательное, он будет содержать дополнительный код этого числа. В табл. 2.10 запись в дополнительном коде положительных и отрицательных чисел. Заметим, что все положительные числа имеют 0 в старшем бите, остальные биты составляют двоичное число. Все отрицательные числа имеют 1 в старшем разряде. Рассмотрим строку +0 в табл. 2.10: запись в дополнительном коде +0 будет 0000 0000. В ближайшей нижней строке видим, что запись в дополнительном коде — 1 следующая: 1111 1111. Рассмотрим пошаговое перемещение в обратном направлении от 0000 0000 до 1111 1111.

Какой будет запись в дополнительном коде числа —9? Рассмотрим этапы преобразования. Они следующие:

Десятичное число 9 Этап 1. Запись десятичного числа без знака (9)

Двоичное число 0000 1001 Этап 2. Преобразование десятичного числа в двоичный код (0000 1001)

Дополнение до 1 1111 0110 Этап 3. Получить обратный код двоичного числа заменой нулей единицами, а единиц —нулями (1111 0110) (обратный или ин версный код)

Дополнение до 2 +1 Этап 4. Прибавить единицу к обратному коду. Здесь прибавить -1 к 1111 0110, что дает

(дополнительный 11110111 11110111

код)

Полученный результат является дополнительным кодом положительного десятичного числа. В приведенном примере дополнительным кодом числа 9 является 1111 0111. Заметим, что знаковый бит —1, это означает, что рассматриваемое число (1111 0111) отрицательно.

Каким будет десятичный эквивалент числа 1111 0000, записанного в форме дополнительного кода? Процедура преобразований в это случае следующая:

Дополнительный код 1111 0000 Этап 1. Запись дополнительного кода (1111 0000).

Дополнение до 1 0000 1111 Этап 2. Получается обратный код дополнительного кода заменой нулей единицами единиц нулями(0000 1111)

Двоичное число +1 Этап 3.Добавить 1 0001 0000=16

Таким образом, формирование обратного кода и добавление 1 являются теми же процедурами, которые мы проводили при преобразовании двоичного числа в дополнительный код. Однако следует отметить, что, хотя мы получили двоичное число 0001 0000= 16₁₀ , исходная запись дополнительного кода 1111 0000= -16₁₀ , т.е. имеем отрицательное число, поскольку старший бит в дополнительном коде является 1.

Упражнения

2.32. Когда числа со знаком помещаются в 8-разрядный регистр микропроцессора, старший (7-й) бит называется___ 2.33. Установить, являются ли следующие числа в дополнительном коде положительными или отрицательными:

а) 0111 0000; б) 1100 1111; в) 1000 1111; г) 0101 0101.

2.34. Используя табл. 2.10, дать дополнительный код следующих десятичных чисел со знаком: а) +1; б) -5; в) +127; г) -1; д) -2; е) -128.

2.35. Используя процедуру, приведенную в § 2.6, дать дополнительный код следующих десятичных чисел со знаком: а) —10; б) —21; в) —34; г) —96.

2.36. Расположение бит в дополнительном коде_______ (в ДДК, в двоичном коде) одинаково для положительных двоичных чисел.

2.37. Используя процедуру, приведенную в § 2.6, дать десятичные эквиваленты следующих чисел в дополнительном коде: а) 1111 1011; б) 0000 1111; в) 1000 1111; г) 0111 0111.

Решения

2.32. Знаковым. 2.33. а) 0111 0000 в дополнительном коде положительно, так. как знаковый бит — 0; б) 1100 1111 в дополнительном коде отрицательно, так как знаковый бит—1; в) 1000 1111 в дополнительном коде отрицательно, так как знаковый бит—1; г) 0101 0101 в дополнительном коде положительно, так как знаковый бит—Д 2.34. См. табл. 2.10: а) +1=0000 0001; б) +5=0000 0101; в) +127=0111 1111; г) —1 = 1111 1111; д) —5=1111 1110; е) —128 = 1000 0000. 2.35. В соответствии с рекомендациями § 2.6 имеем следующие результаты: а) этап 1 (преобразование десятичного числа в двоичный код): 10₁₀= 0000 1010₂; этап 2 (получение обратного кода): 0000 1010-1111 0101; этап 3 (добавление 1): 1111 0101 + 1 = 1111 0110 (доп. код); б) этап 1: 21₁₀=0001 0101₂; этап 2: 0001 0101-1110 1010; этап 3: 1110 1010+1 == 1110 1011 (доп. код); в) этап 1: 34₁₀=0010 0010₂; этап 2: 0010 0010₂-1101 1101; этап 3: 1101 1101+1 = 1101 1110 (доп. код); г) этап 1: 96₁₀=01100 0000₂; этап 2: 0110 0000₂-1001 1111; этап 3: 1001 1111+ 1 = 1010 0000 (доп. код). 2.36. В двоичном коде. 2.37. а) 1111 1011(доп. код) =— 5₁₀ б) 0000 1111 (доп. код) =+15; в) 1000 1111 (доп. код) = -113; г) 0111 0111 (доп. код)=+ 119