Емкостной элемент схемы замещения электрической цепи.

Из физики известно, что i(t)=CdU_c (t)/dt, тогда

U_с(t)=(1/C) ò i(t)dt=(1/wC)×I_m (-coswt)=X_c I_m sin(wt-p/2)=U_m sin(wt-p/2),

где X_c=1/wC - ёмкостное сопротивление,

U_m=X_С I_m - амплитуда напряжения на ёмкостном сопротивлении.

Напряжение на конденсаторе отстаёт от тока на p/2.

+j

I

UC

i(t)

uc(t)

0

C

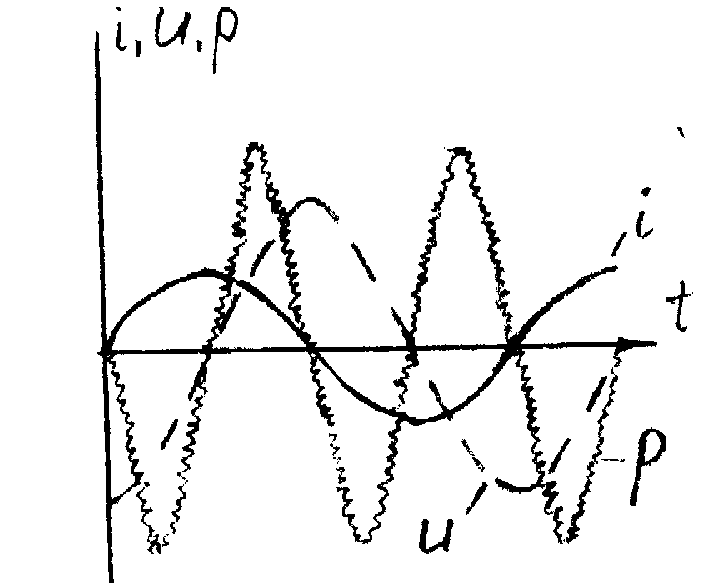
Рис 5.10. Векторная диаграмма тока и напряжения для ёмкости.

Рис 5.11. Зависимости тока, напряжения и мощности на ёмкости.

Мгновенная мощность на конденсаторе p_c(t)= I_m U_m /2(-sin2wt)

Из графиков для L и C следует, что в 1-ю четверть периода Р на индуктив­ности положительна Þ индуктивность потребляет энергию из источника , а Р на конденсаторе отрицательна Þ конденсатор в эту четверть периода отдаёт энергию источнику.

Тестовые вопросы по теме

1) Что называется переменным током.

2) Мгновенные значения тока, напряжения и ЭДС (определение и формула).

3) Что называется фазой, начальной фазой, единицы измерения фазы.

4) Что называется действующим значением переменного тока. Формула.

5) Три формы записи комплексного числа.

6) Что называют поворотным множителем

7) Что такое комплексно сопряжённое число.

8) Записать комплексные функции времени тока и напряжения.

9) Что называется векторной диаграммой.

10) Записать амплитудное и действующее значение тока

11) Что такое векторная диаграмма, как она строится?

12) Три формы записи комплексного числа.

13) Активное сопротивление в цепи синусоидального тока. Векторная диаграмма его.

14) Индуктивное сопротивление. Формула. Векторная диаграмма тока и напряжения на катушке индуктивности.

15) Ёмкостное сопротивление. Формула. Векторная диаграмма тока и напряжения на конденсаторе.

Лекция 6.

Последовательное соединение L,C,R на переменном токе. Комплексное сопротивление и резонанс напряжений.

Z= R+j(X_L –X_C)=R+j(wL-1/wC) – комплексное сопротивление,

Z= R+jX- алгебраическая форма записи комплексного числа,

X= X_L –X_C.– реактивное сопротивление.

Z=z×e^jj - показательная форма записи,

z=Ö(R²+X²)- модуль комплексного сопротивления,

j=arctg(X/R)=arcsin(X/Z)=arcos(R/Z)-аргумент комплексного сопротивления. Для определения аргумента желательно использовать arctg(X/R)и arcsin(X/Z), т.к. cos – функция чётная и нельзя определить знак

+j

+1 R

Z R

R R

R

X R

Если параметры цепи подобраны таким образом, что справедливо |Lw|>|1/Cw|, то X>0 и j>0 и напряжение опережает ток на j= arctg(X/R) – цепь носит индуктивный характер (X_L>X_C). Если справедливо |Lw|<|1/Cw|, то X<0, j<0, напряжение отстает от тока. В этом случае принято говорить, что цепь имеет емкостный характер (X_L<X_C).

Рис. 6.1. Векторная диаграмма сопротивлений.

Резонанс напряжений .

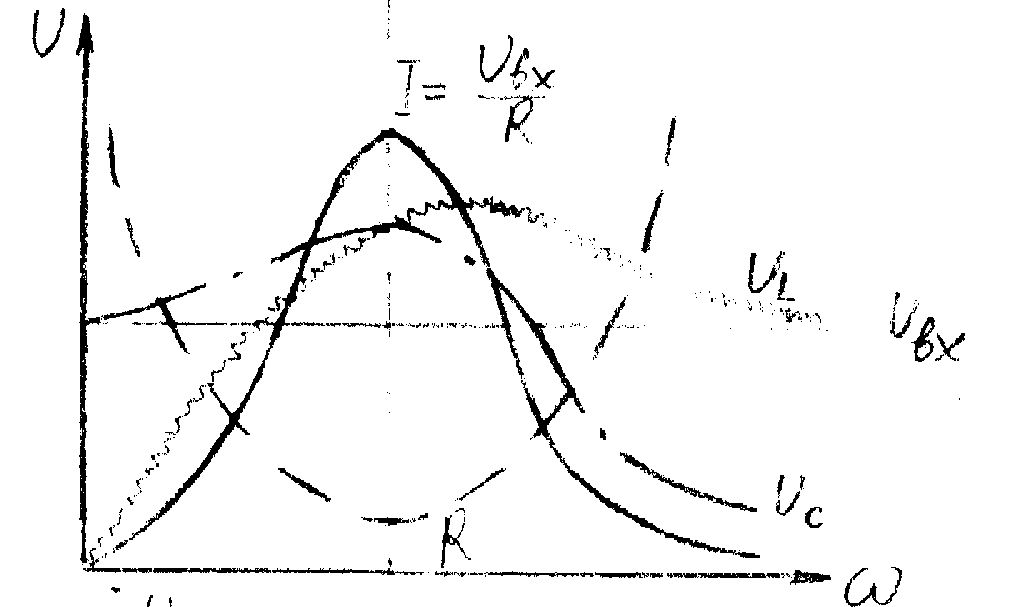
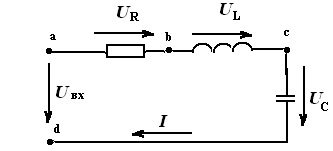
Рис. 6.2. Схема последовательной RLC цепи и зависимости тока и напряжений на элементах схемы от частоты.

1. u(t)= u_R(t)+ u_C(t)+ u_L(t) – закон Кирхгофа для мгновенных значений?

U_вх=U_R+Uc+U_L – для комплексных значений.

2. Z= R+j(X_L –X_C )

3. I∙Z=I∙R+jI∙X ; гдеX=X_L-X_C

4. Uвх =U_R +j(U_L-Uc) – входное напряжение

5. I²Z=I²R+jI²X; Мощность цепи - S=P+jQ

S= 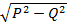–полная мощность

P=I²R=Scosj= 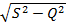- активная мощность

Q= I²X= Ssinj= 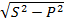- реактивная мощность.

При изменении частоты входного сигнала может быть: X_L=X_C; wL=1/wc. В этом случае сопротивление будет носить чисто активный характер Z=R, и ток в контуре будет совпадать по фазе с выходным напряжением: I=U_вх/R. Такое явление называется резонансом.

w=w_р= 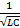=2pf, f_р= 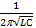(в опытах f=50 Гц).

Ток будет максимальным и будет определяться активным сопротивлением, когда частота равна f_р (резонансная).

Когда частота равна 0, сопротивление X_C=∞, ток равен 0, Uс=U_вх. С увеличением частоты I растет, Uc - растёт, затем спадает. Если сопротивление R мало, то при резонансе напряжений ток в цепи резко возрастает по сравнению со значениями тока при частоте отличной от f_р. Одновременно U_L и U_C могут превысить напряжение питания U. Такое превышение получается если:

U_L = U_C = I∙wL = I/wc >U_вх , wL = 1/wC>R

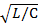>R – условие превышения напряжения на реактивных элементах по сравнению с входным напряжением.

При резонансе U_L=U_C , IZ=IR+jIX

Ток в цепи одинаковый, тогда U_L и U_C>U_вх

При резонансе: IZ=IR+jIX_L –jIX_C, X_L=X_C и Uвх =IR

Вывод: напряжение на индуктивном и ёмкостном сопротивлениях больше, когда X_L=X_C>R,

u_вх(t)=u_R(t)+u_C(t)+u_L(t) -мгновенное значение напряжения на элементах цепи.