Символический метод расчёта.

При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд, в котором синусоидально изменяющиеся функции изображаются векторами на комплексной плоскости. Комплексный метод расчёта, предложил в 1893-1897гг. Чарльс Протеус Штейнмец. Из курса математики известно, что комплексное число может быть записано в показательной или алгебраической форме:

,

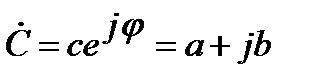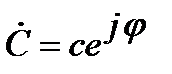
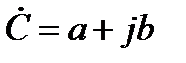
где с - модуль комплексного числа; φ- аргумент; a=Re( 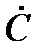) – действительная часть; b=Im( 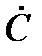) - мнимая часть; j - мнимая единица, j = .

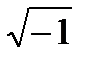С помощью формулы Эйлера можно перейти от показательной формы записи комплексного числа к алгебраической:

;

; .

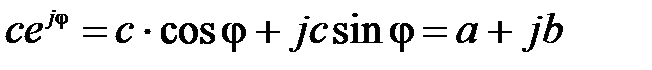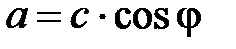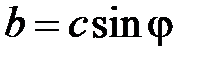От алгебраической формы записи переходят к показательной форме с помощью формул:

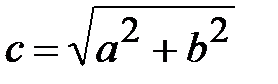; φ=arctg .

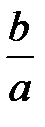Комплексное число может быть представлено в виде радиус - вектора на комплексной плоскости с длиной, равной модулю c, расположенного в начальный момент времени под углом φ относительно вещественной оси (рис.5.5).

Рис 5.5. Векторное обозначение комплексного числа.

Умножим комплексное число на множитель e^jβ. Радиус - вектор на комплексной плоскости повернется на угол βпротив часовой стрелки. Множитель e^jβ называется поворотным:

.

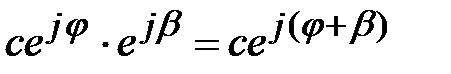Отметим очевидные соотношения при следующих значениях угла β:

,

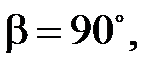
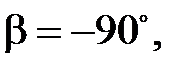
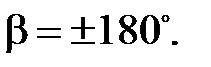
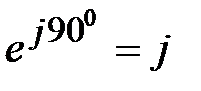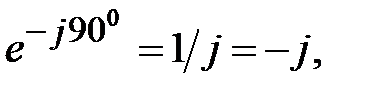
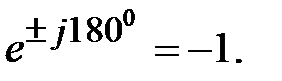
Умножение вектора на j является операцией его поворота в сторону опережения на 90^о (против часовой стрелки) по отношению к исходному вектору, умножение на (-j) – соответственно поворот его на 90^о в сторону отставания. Умножение вектора на -1(смена знака) означает его поворот на 180^о в любом направлении поворота.

Два комплексных числа, имеющие равные модули и равные, но противоположные по знаку аргументы, называют комплексно сопряжёнными числами. Если исходное комплексное число 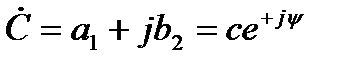, то комплексно сопряжённым числом будет .

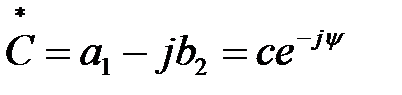Свойства комплексно сопряжённых чисел:

;

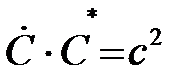Re( 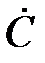)=( )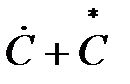/2, Im( 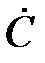)=( )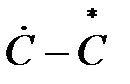/2j.

Если 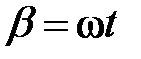, то вектор, умноженный на 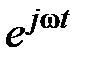, превратится во вращающийся со скоростью ωрадиус-вектор.

Выражение 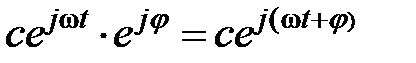является комплексной функцией времени. Применительно к синусоидальным напряжениям и токам получим их комплексные функции времени:

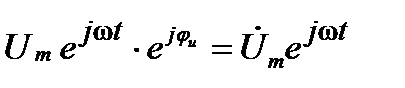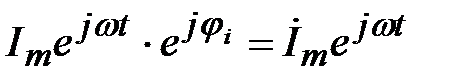, , (2.5)

где 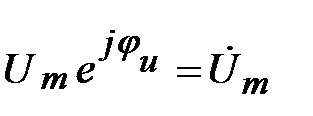, 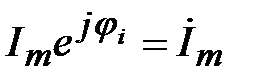- комплексные амплитуды напряжения и тока (исходное положение векторов в комплексной плоскости).

Найдем мнимую часть комплексной функции времени для напряжения.

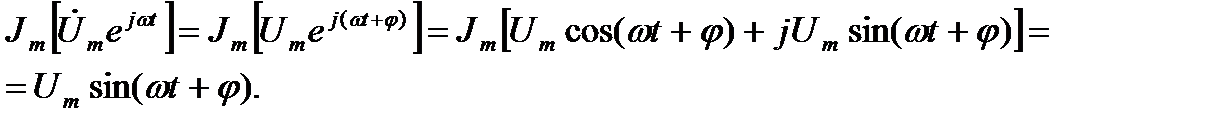
Мгновенное синусоидальное напряжение (ток, напряжение, ЭДС) является мнимой частью соответствующей комплексной функции времени.

Таким образом, синусоидальные функции времени могут быть представлены векторами в комплексной плоскости, вращающимися против часовой стрелки с постоянной угловой скоростью ω, проекции которых на мнимую ось изменяются по синусоидальному закону.

Для единообразия принято на комплексной плоскости изображать вектора синусоидально изменяющихся во времени величин для момента времени .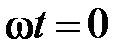

При расчетах цепей вместо комплексных амплитуд токов и напряжений используют комплексные действующие значения, которые в 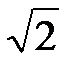раз меньше. Совокупность векторов на комплексной плоскости, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты, называют векторной диаграммой.