Построение векторных диаграмм.

UR R

Uвх R

j

UL R

+j

I

+1 R

UC R

R

UX R

Рис. 6.3. Векторная диаграмма напряжений на элементах схемы.

По действительной оси откладываем величину общую для всех элементов цепи. Для последовательного соединения это будет – ток. Ток откладывается в одном масштабе, а напряжение в другом. Масштаб напряжения и масштаб тока могут не совпадать.

j- угол сдвига между током и напряжением, j=arctg(X_L-X_C)/R

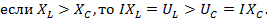
juR

jI R

jI R

I

UC R

Uвх=UR R

UL R

+j

I

+1 R

UC R

R

a) R

b)

I

UR R

Uвх R

UL R

j

+j

+1 R

R

Рис. 6.4. Векторная диаграмма напряжений на элементах схемы

при резонансе a) и отсутствии его b), во втором случае начальная фаза тока больше нуля.

Если U_L=U_c, то U_R=U_вx , если X_L<X_C, то U_L< U_C.

j_I – начальный угол тока,

j – угол сдвига между I и U,

j_u – начальный угол напряжения.

Топографическая диаграмма –векторная диаграмма, построения по определенным правилам.

Для этого определяют комплексное значение потенциалов точек (всех) относительно одной, потенциал которой принимается за 0. При этом любому потенциалу будет соответствовать своя точка на комплексной плоскости. Переносят комплексные значения потенциалов на комплексную плоскость и рисуют соответствующие вектора.

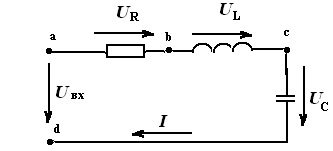
Рис. 6.4. Схема последовательной RLC цепи.

b

UC

I

c

Uвх

Uab

UL

UR

a

d

+1

+j

Рис. 6.5. Топографическая диаграмма RLC цепи.

Принимаем потенциал узла j_a=0. Проводим вектор U_Rпо направлению тока, т.к. направление U_R всегда совпадает с направлением I. Попадаем в точку (b). От этой точки откладываем вектор U_L , попадаем в точку (с). От этой точки откладываем вектор U_C и попадаем в точку (d). Соединив точки a и d получим вектор входного напряжения U_вх . В топографической диаграмме можно определить разность потенциалов между другими точками, например, между a и c.

При подключении вольтметров к элементам вышеприведённой схемы может оказаться, что второй закон Кирхгофа не выполнятся. Сумма показаний вольтметров на элементах схемы может быть больше показания вольтметра входного. Дело в том, что вольтметры показывают действующее значение напряжения, а складывать нужно вектора. Вольтметр показывает только длину вектора, но не его направление.

Тестовые вопросы по теме

1. Активное, реактивное и полное комплексное сопротивления цепи. Треугольник сопротивлений. Векторная диаграмма напряжений и токов.

2. Активная, реактивная, полная и комплексная проводимость цепи. Треугольник проводимостей. Векторная диаграмма напряжений и токов.

3. Резонансные явления в электрических цепях при последовательном соединении R,L,C - элементов, условия резонанса, векторная диаграмма, резонансные кривые.

4. Добротность, физический смысл добротности.

5. Полное комплексное сопротивление цепи. Формула.

6. Треугольник сопротивлений.

7. Что называется резонансом в электрических цепях.

8. Условие наступления резонанса напряжений.

9. Как можно добиться режима резонанса в последовательной цепи (какие параметры схемы изменять).

10. Нарисовать цепи, в которых можно наблюдать резонанс напряжений.

11. При каком условии напряжения на реактивных элементах схемы будут превышать входное напряжение.

12. При каком условии напряжения на реактивных элементах схемы по величине будут меньше входного напряжения.

13. При каком условии напряжения на реактивных элементах схемы будут по величине равны входному напряжению.

14. К источнику синусоидального напряжения u(t)=U_mSinωt подключены, последовательно соединённые резистор и конденсатор, к которым подключены вольтметры электромагнитной системы. На сопротивлении вольтметр показывает 9 В, на конденсаторе - 12 В. Определить U_m.

15. На вход последовательного RLC контура подано напряжение u(t)=141Sin628t, параметры контура: R = 10 Ом, L = 25,5 мГн, С = 398 мкФ. Определить падения напряжения на элементах контура.

16. К источнику синусоидального напряжения u(t)=U_mSinωt подключены, последовательно соединённые резистор и индуктивность, к которым подключены вольтметры электромагнитной системы. На сопротивлении вольтметр показывает 8 В, на конденсаторе - 6 В. Определить U_m.

17. На вход последовательного RLC контура подано напряжение u(t)=141Sin628t, параметры контура: R = 100 Ом, L = 25,5 мГн, С = 398 мкФ. Определить падения напряжения на элементах контура.

18. Определить модуль полного сопротивления цепи, состоящей из последовательно соединённых RLC элементов с номиналами: R = 10 Ом, X_L = 21 Ом, X_C = 11 Ом.

19. Определить угол сдвига между током и напряжением в цепи, состоящей из последовательно соединённых RLC элементов с номиналами: R = 10 Ом, X_L = 21 Ом, X_C = 11 Ом.

Лекция 7.

Резонанс токов.

б)

0

t

0

Z R

R

I1,I2,I R

I2

I2

I

I1

Z R

Z R

Z R

I

Uвх R

L

R1

C

R2

Z R

I1 R

L

R1

C

R2

I1 R

I2 R

I2 R

Рис. 7.1. Схема параллельной RLC цепи а) и временные

диаграммы её параметров б).

Явление резонанса в схеме, образованной двумя параллельными ветвями с разнохарактерными реактивными сопротивлениями называется резонансом токов.

Ток I₁ отстает от напряжения, I₂ опережает его.

Обозначим: комплексную проводимость

Y = 1/Z = 1/(R+jx) = (R-jx)/(R²+x²)= g – jb = Ye^-jj

где: g = 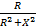– активная проводимость;

b = 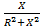– реактивная проводимость;

Y = 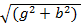– модуль полной комплексной проводимости;

j = arctg(b/g) = arccos(g/Y) = arcsin(b/Y) – аргумент комплексной проводимости.

Полная проводимость между точками a и b будет иметь вид:

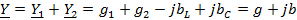
где: = ; = .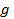

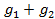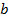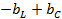Полное сопротивление цепи будет иметь вид

Z = = ,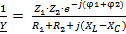

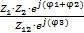Здесь в знаменателе:

Z₁+Z₂=R₁+R₂+j(X_L-X_C )=R+jX=Z₁₂∙e^jj3 ,

R₁+R₂=R – активное сопротивление,

X_L-X_C=X - реактивное сопротивление,

Z₁₂= 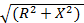⁾- модуль комплексного сопротивления;

j₃=arctg (X/R)аргумент комплексного сопротивления.

Тогда, исходя из вышеизложенного, формула полного сопротивления примет вид:

Z₁₂ .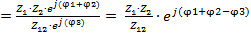

Uвх R

а)

I1

I2

U

+j

Рис. 7.2. Векторная диаграмма (качественная) параллельной цепи.

Если активные сопротивления равны 0, то токи под прямым углом (j₁=j₂=90⁰) нет резонанса токов.

В этой схеме резонанс наступает, когда модули реактивных проводимостей равны между собой (b₁=b₂).

I=I₁ +I₂; I₁=U_abY₁=U_ab(g₁-jb₁)

I₂=U_abY₂=U_ab(g₂+jb₂)

Y₂=(R+jX₂)/[(R-jX₂) (R+jX₂)]

Y₁=1/(R₁+jX₁)

X₁=X_L; X₂=X_C

Резонанс: (|b₁|=|b₂|-условие параллельного резонанса);

I=U((g₁ +g₂)+j(b₁-b₂))

w_p=w₀∙ 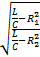– резонансная частота,

w₀= 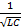- резонансная частота идеального контура,

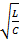=ρ - волновое сопротивление контура.

Резонанс – явление при котором ток в не разветвлённой цепи контора совпадает с напряжением подаваемым на этот контор ( ток с выхода генератора совпадает по фазе с напряжением).

Если R₁=R₂=0, то w_p=w₀= 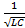и контор называется идеальным и его входное сопротивление при резонансе Z_вх=¥.

+1

I

C

Рис. 7.3. Схема идеального LC контура.