Метод узловых потенциалов.

Основан на применении 1-го закона Кирхгофа

Е1

R1

R7

J6

R6

Е2

R2

R3

R4

R5

a

b

c

d

Рис. 4.9. Эквивалентная схема к расчёту по методу узловых потенциалов.

Составить уравнения по методу узловых потенциалов для узлов a,b,c. Потенциал узла dприравниваем к 0 (рис. 4.8).

Для узла a:

j_a(1/(R₁+R₇)+1/R₃+1/R₄+1/R₅)-j_b(1/R₃+1/R₄)-j_c(1/(R₁+R₇))=

=E₁/(R₁+R₇)+E₃/R₃=I_a.

Для узла b:

-j_a(1/R₃+1/R₄)+j_b(1/R₃+1/R₄+1/R₂)=E₂/R₂-E₃/R₃₌I_b.

Для узла с:

-j_a/(G₁+G₇)+j_c(1/(G₁+G₇)+1/G₆)=-E₁/(G₁+G₇) - J=I_c.

В общем виде уравнение для к-го узла:

j_{k 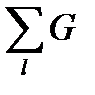kl}- j_{i 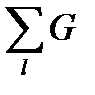kl}= + _k

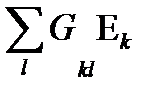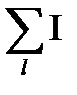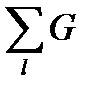_kl-проводимость.

j_k-потенциалк-го узла.

åG_kl-сумма узловых проводимостей к-го узла, представляя собой сумму проводимостей ветвей, подключенных к к-му узлу. Это собственная про­водимость к-го узла.

åI_k-алгебраическая сумма источников токов ветвей, подключённых к к-тому узлу.

åE_kG_kl-алгебраическая сумма произведений E ветвей, сходящихся в к-м узле на проводимости этих ветвей.

Правило:

Если Е и ток источника направлены к узлу, то в правой части уравнения берётся знак ²+².

I. j_a(1/(G₁+G₇)+1/G₃+1/G₄+1/G₅)-j_b(1/G₃+1/G₄)-j_c/(G₁+G₇)=

=E₁/(G₁+G₇)+ +E₃/G₃=I_a

-j_a( 1/G₃+1/G₄)+j_b( 1/G₃+1/G₄+1/G₂)= E₂/G₂- E₃/G₃=I_b

- j_a/(G₁+G₇)+j_c(1/(G₁+G₇)+1/G₆)= -E₁/(G₁+G₇)-I=I_c

или

II. j_a×G_aa+j_b×G_ab-j_c×G_ac=I_a

j_a×G_ba+j_b×G_bb=I_b

j_a×G_ca+j_c×G_cc=I_c

Решая систему относительно потенциалов. Токи в ветвях определяется разностью потенциалов между узлами по следующим формулам:

I₁=(j_c-j_a+E₁)G₁ I₄=(j_a-j_b)G₄

I₂=(j_b-E₂)G₂ I₅=G₅j_a

I₃=(j_a-j_b-E₃)G₃ I₆=G₆j_c

Тестовые вопросы по теме.

1. Назовите основные методы расчёта электрических цепей.

2. Что такое простая цепь, определение, пример схемы.

3. Расчёт схем по методу свёртывания и раз­вертывания, алгоритм.

4. Расчёт схем по методу наложения, алгоритм.

5. Расчёт схем по уравнениям Кирхгофа, алгоритм.

6. Расчёт схем по методу контурных токов, алгоритм.

7. Расчёт схем по методу узловых потенциалов, алгоритм.

8. Расчёт схем по методу эквивалентного двухполюсника, алгоритм.

9. Что такое собственная проводимость узла?

Лекция 5.

Переменный ток.

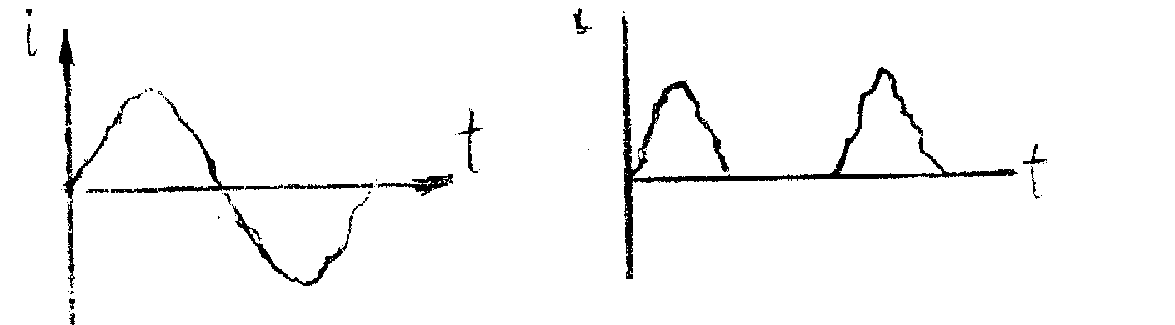
Переменным током называется ток, величина и направление которого изменяются во времени.

а) переменный ток, б) импульсный ток

Рис 5.1. Графические изображения переменного и импульсного токов:

Мгновенное значение переменного тока определяется выражением:

где: I_m - амплитуда, w = 2pf (с^-1) - круговая частота,

f = 1/T (Гц) – циклическая частота, Т – период, j_i - начальная фаза

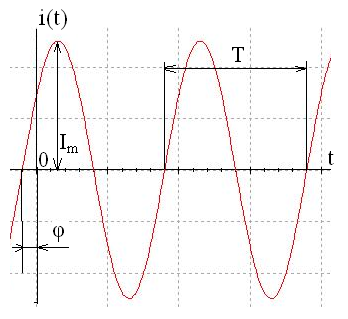
Рис 5.2. Осциллограмма синусоидального тока.

Если начало синусоиды сдвинуто влево относительно начала отсчёта (0), т.е. синусоида в момент времени, равный нулю, имеет положительное значение, то начальная фаза – положительна. Если начало синусоиды сдвинуто вправо относительно начала отсчёта (0), т.е. синусоида в момент времени, равный нулю, имеет отрицательное значение, то начальная фаза – отрицательна.