Случайные величины (повторение из курса ТВИМС)

Определение 1.4.1. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно. Пусть опыт – сеанс игры в кости (кость – кубик, рис. 1.5). Суть игры состоит в выбрасывании кубика (кубиков) и дальнейшем подсчёте очков на верхней грани кубика, количество которых и определяет победителя. Разновидности игры предполагают разный подсчёт очков. Итак, до опыта (выбрасывания кубика, a priori) мы не знаем число очков, которое выпадет на верхней грани кубика. После опыта (a posteriori) верхней гранью кубика может быть одна из граней, показанная на рис. 1.4 [10, 11].

или- или- или

Рисунок 1.4 – Варианты верхних Рисунок 1.5 – Кубик (кость) для

граней кубика, которые могут выпасть игры в кости

при его бросании при игре в кости

2-й вариант определения 1.4.1. Переменная величина называется также случайной, если в результате опыта она может принимать действительные значения с определёнными вероятностями.

Определение 1.4.2. Вероя́тность – степень (относительная мера, количественная оценка) возможности наступления некоторого события [10, 12]. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае – маловероятным или невероятным.

В теории вероятностей и математической статистике понятие вероятности формализуется как числовая характеристика события – вероятностная мера (или её значение) – мера на множестве событий (подмножеств множества элементарных событий), принимающая значения от 0 до 1. Значение 1 соответствует достоверному событию. Невозможное событие имеет вероятность 0 (обратное, вообще говоря, не всегда верно). Если вероятность наступления события равна p, то вероятность его ненаступления равна 1-p. В частности, вероятность 1/2 означает равную вероятность наступления и ненаступления события. Простой пример для игры в кости: вероятность того, что на кубике, показанном на рис. 1.5, выпадет число «5» (как на рис. 1.5), равна при равновероятных исходах бросания 1/6 (так же, как и для любого другого числа на кубике).

Простейший подсчет вероятности наступления единичного случайного равновероятного (равновозможного) события. Классическое определение вероятности основано на понятии равновозможности исходов. В качестве вероятности выступает отношение количества исходов, благоприятствующих данному событию, к общему числу равновозможных исходов. Например, вероятность выпадения «орла» или «решки» при случайном подбрасывании монетки равна 1/2, если предполагается, что только эти две возможности имеют место, и они являются равновозможными. Предположим, вы хотите выяснить насколько вероятно событие «выпадение числа «пять» на игральной кости с 6-ю сторонами (рис. 1.4) [10, 13]. «Выпадение пятёрки» – это событие, а 6 – это число возможных исходов. Вот еще несколько примеров, которые помогут вам разобраться:

Пример 1: Какова вероятность выбрать выходной день, случайно выбирая число? «Выбор выходного дня» – это событие, а число возможных вариантов равняется числу дней в неделе – семи.

Пример 2: В банке с мармеладом находится 6 синих, 10 красных и 4 белых мармеладных шарика. Если предположить, что шары перемешаны и вытаскиваются случайным образом, какова вероятность вытащить красный? «Вытащить красный» – это событие, а число возможных исходов равняется числу шариков в банке, 20.

Алгоритм простейшего подсчета вероятности наступления единичного случайного равновероятного (равновозможного) события: разделите число желаемых событий на общее число возможных событий. Вы получите вероятность происшествия единичного события. В случае с выпадением числа «пять» на игральной кости (на игральной кости только одна «пятёрка»), вероятность можно выразить 1/6, 0.166, или 16.6%. Простейший подсчет вероятности наступления единичного случайного равновероятного (равновозможного) события для других примеров приведен ниже:

Пример 1: Какова вероятность выбрать выходной день, случайно выбирая число?

Так как в неделе два выходных, то число желаемых событий будет 2, а число возможных событий равно 7. Вероятность будет равна 2/7, или 0.285, или 28.5%.

Пример 2: Какова вероятность вытащить красный шарик?

Число желаемых событий равняется количеству красных шариков в банке – 10, общее число событий равняется 20. Вероятность будет равна 10/20 =1/2, или 0.5, или 50%.

Дополнительные вопросы по рассмотренной тематике («Вычисление вероятности множества случайных событий», «Как перевести шансы в вероятность», «Формула полной вероятности» [11–13]) студентам предлагается повторить самостоятельно.

Всё вышесказанное относится к дискретным (прерывным) случайным величинам.

Определение 1.4.3. Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения Х=х_i, которые можно перенумеровать [10, 11].

Р(Х=х_i)=p_i, i=1, 2 , 3…, 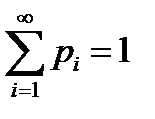(1.1)

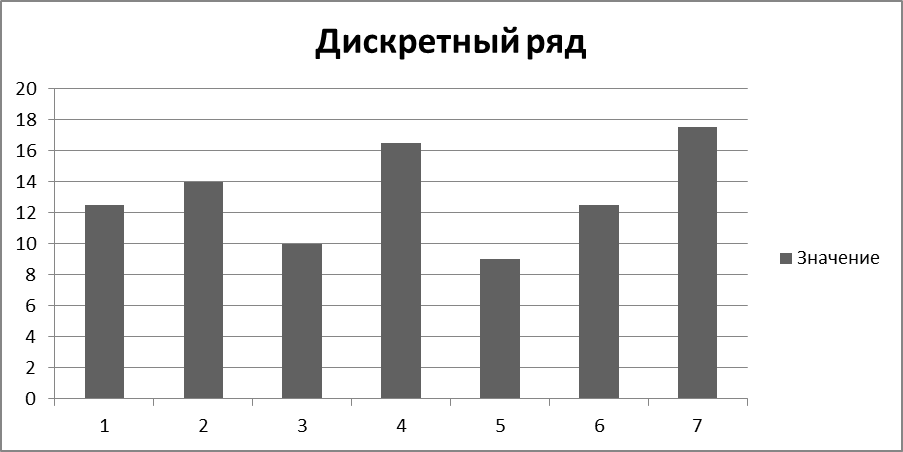
На рис. 1.6 показано представление дискретной случайной величины, зависящей от времени, в виде дискретного ряда.

Определение 3.4. Случайная величина Х называется непрерывной, если для любых a<b существует такая неотрицательная функция f(x), что [10, 11]

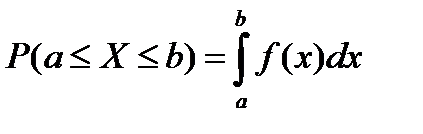(1.2)

Другими словами, непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток.

Время

Рисунок 1.6 – Представление дискретной случайной величины, зависящей от времени, в виде дискретного ряда

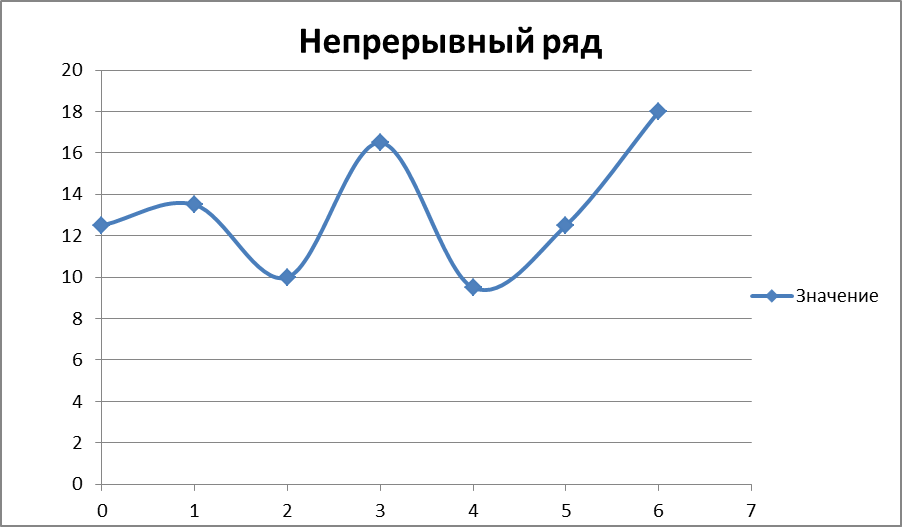
На рис. 1.7 показано представление непрерывной случайной величины, зависящей от времени, в виде непрерывного ряда.

Время

Рисунок 1.7 – Представление непрерывной случайной величины, зависящей от времени, в виде непрерывного ряда

Функция f(x) называется плотностью распределения непрерывной случайной величины. Вероятность того, что случайная величина Х (дискретная или непрерывная) принимает значение, меньшее х, называется функцией распределения случайной величины Х и обозначается F(x):

F(x) = Р(Х˂х) (1.3)

Функция распределения является универсальным видом закона распределения, пригодным для любой случайной величины. Закон распределения является наиболее полной, исчерпывающей характеристикой случайной величины. Закон распределения – функция (таблица, график, формула), позволяющая определять вероятность того, что случайная величина Х принимает определенное значение х_i или попадает в некоторый интервал. Если случайная величина имеет данный закон распределения, то говорят, что она распределена по этому закону или подчиняется этому закону распределения. Общие свойства функции распределения:

1) F(x) – неубывающая функция, т. е. при х₂ ˃ х₁ F(x₂) ≥ F(x₁),

2) F(x) – ограниченная функция, т. е. 1 ≥ F(x) ≥0,

3)

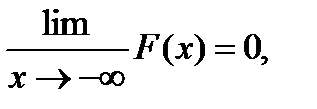
4)

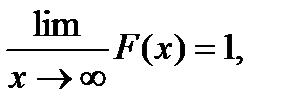
Дискретный ряд, показанный на рис 1.6, является частным видом закона распределения для дискретных случайных величин. Основные свойства плотности распределения:

1) f(x) ≥ 0,

2)

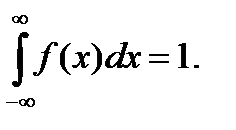
Таким образом, законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Общая взаимосвязь между случайными величинами и законами их распределения показана на рис. 1.8.

Случайная величина

Непрерывная

Дискретная

Законы распределения

Ряд распределения

Плотность распределения

Функция распределения

Рисунок 1.8 – Взаимосвязь между случайными величинами и законами их распределения