Основные характеристики модели отказа и их расчёт

ДЗР удобно характеризовать некоторыми временными характеристиками, именуемыми характеристиками положения или характерными точками распределения, а также вторым моментом (дисперсией), характеризующей разброс случайной наработки относительно важнейшей характеристики положения – математического ожидания M(t) (м. о.) наработки t до отказа. Для непрерывной случайной наработки t до отказа её м.о. (первый момент) равно

(1.9)

а дисперсия –

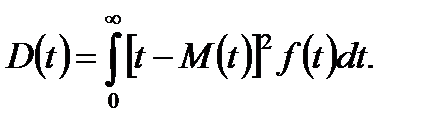(1.10)

Среднеквадратичное отклонение σ (с. к. о.) есть корень из дисперсии, т. е.

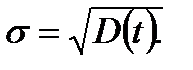(1.11)

Модой t_M непрерывной случайной наработки t является то её значение, в котором плотность распределения f(t) максимальна: 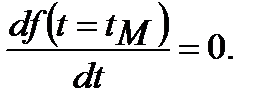(1.12)

В общем случае симметричного распределения м.о. его и его мода не совпадают. Медианой t_MЕ непрерывной случайной наработки t называют такое её значение, для которого

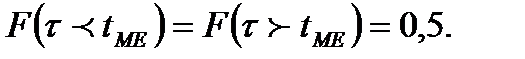(1.13)

Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой f(t), делится пополам.

Расчёт статистических характеристик модели отказа прерывной случайной наработки или времени восстановления t_k проводится для N их значений (k=1, 2, ... N) по следующим формулам:

1.6.1 Математическое ожидание

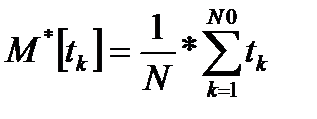(1.14)

1.6.2 Дисперсия

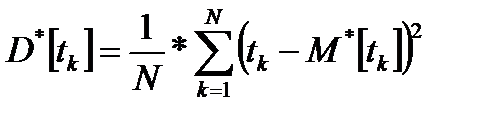(1.15)

1.6.3 Среднеквадратичное отклонение 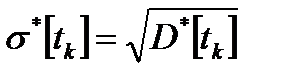(1.16)