Основные модели отказов и их характеристики. Основные свойства моделей отказов
Основные модели отказов и их характеристики приведены в табл. 1.1. Следующие свойства моделей отказов следует запомнить:
1.7.1. Экспоненциальное распределение. Является частным случаем распределения Вейбулла и гамма-распределения. Поскольку реальная типичная кривая зависимости интенсивности отказов во времени имеет вид, показанный на рис. 1.2, то экспоненциальное распределение описывает только период нормальной эксплуатации и характеризуется на этом периоде постоянной интенсивностью отказов (см. (1.18)). Последнее показывает, что экспоненциальное распределение абсолютно не учитывает как ранние отказы, так и старение и износ, где его использовать нецелесообразно.
Для экспоненциального распределения при
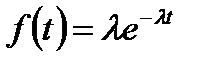 (1.17)
(1.17)
формула (1.5) легко выражается через (1.7)
Таблица 1.1
Основные модели отказов по ГОСТ [7]
| Наименование распределения | М.о. M(t) | Медиана tME | Мода tM | Дисперсия D(t) | С.к.о. 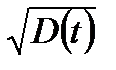
| |
| ДЗР f(t) | модель отказа ИЗР F(t) | |||||
| 0. Равномерное | 0,5 (а+ b) | 0,5 (а+b) | (а+b)21/12 | |||
| С при b>t>а, 0 при t>b, а>t | 0 при а>t, 1 при t>b,
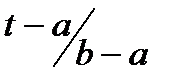 при b>t>а при b>t>а
| |||||
| 1.Экспоненциальное | 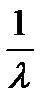
| 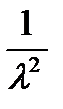
| 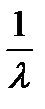
| |||
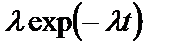
| 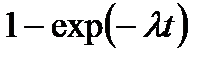
| |||||
| 2. Логарифмически нормальное |
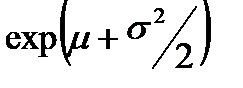
|
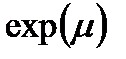
|
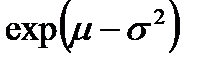
|
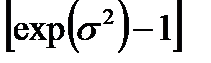 *
* *
* 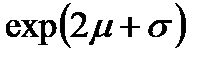
| ||
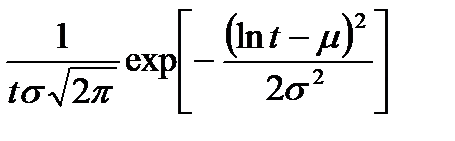
| 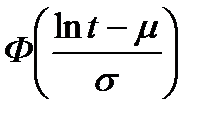
| |||||
| 3. Вейбулла |
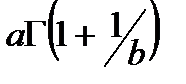
|
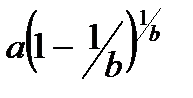
|
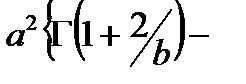
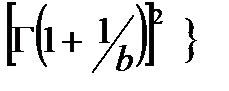
| |||
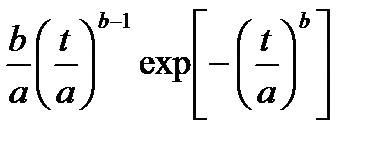
| 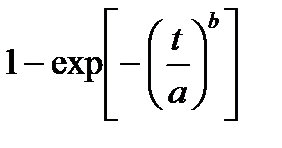
| |||||
| 4. Нормальное | m | m | m | σ2 | σ | |
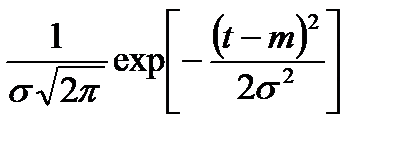
| 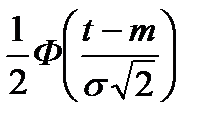
| |||||
| 5. Альфа– распределение (Г.В.Дружинина) |
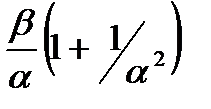
|
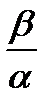
|
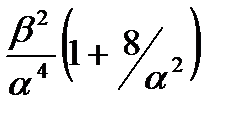
| |||
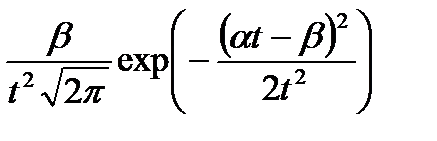
| 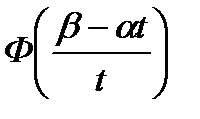
| |||||
| Наименование распределения | М.о. M(t) | Медиана tME | Мода tM | Дисперсия D(t) | С.к.о. 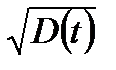
| |
| ДЗР f(t) | модель отказа ИЗР F(t) | |||||
| 6. DM – распределение (диффузионное монотонное) | 
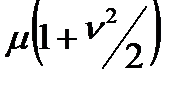
| μ |
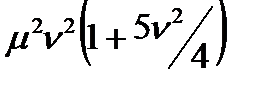
| |||
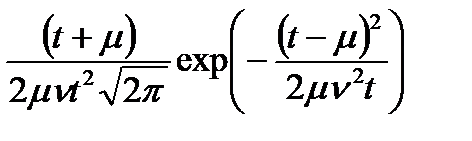
| 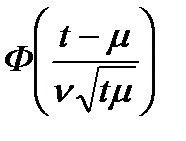
| |||||
8. Гамма-распределение
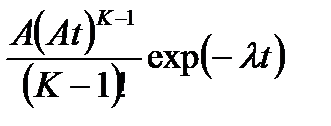
| 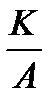
| 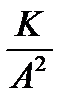
| 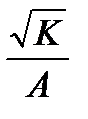
| |||
9. Релея
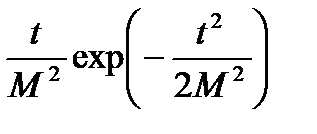
| 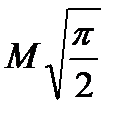
| 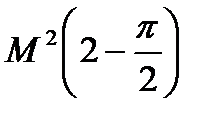
| ||||
| Дискретные распределения: 11. Пуассона | 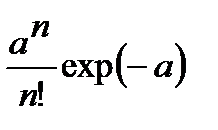
| A | a |
Примечания к табл. 1.1:
* 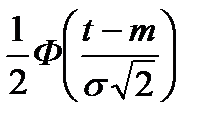 – табличный интеграл вероятностей или интеграл Лапласа, имеющий вид
– табличный интеграл вероятностей или интеграл Лапласа, имеющий вид 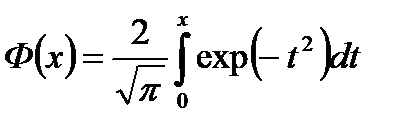
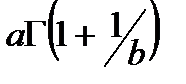 – гамма распределение, имеющее вид
– гамма распределение, имеющее вид
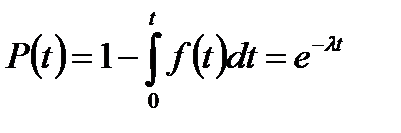
 , (1.18)
, (1.18)
а формула (1.8) – через (1.17) и (1.18)
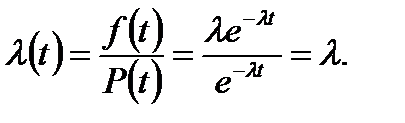 (1.19)
(1.19)
Резко упрощается для экспоненциального распределения формула (1.9)
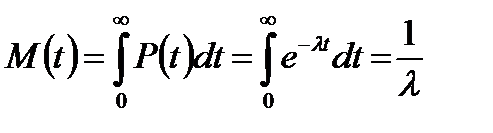 (1.20)
(1.20)
1.7.2. Распределение Вейбулла. Является используемым для кривой интенсивности отказов на периоде ранних отказов (при b<1 интенсивность отказов монотонно убывает) и на периоде ресурсных отказов (при b>1 интенсивность отказов монотонно возрастает). При b=1 распределениеВейбулла превращается в экспоненциальное.
1.7.3. Нормальное распределение. Параметры его m и σ являются математическим ожиданием и среднеквадратичным отклонением распределения, причём всё рассеивание случайной наработки относительно её м.о. m с точностью до долей процента укладывается в интервал [m-3σ, m-3]. Мода и медиана нормального распределения совпадают с его м.о., причём максимальная ордината кривой плотности нормального распределения, соответствующая абсциссе, равной моде, медиане и м. о., составляет 1/2πσ.
Дата добавления: 2016-07-05; просмотров: 2344;











