Динамика исполнительного механизма

Предметом динамики исполнительного механизма является описание действующих на него сил и моментов в форме уравнений динамики. Эти уравнения можно получить на основе ньютоновской или лагранжевой механики.

Для вращательного движения исполнительного механизма эти уравнения, приведенные к валу двигателя, имеют вид

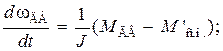
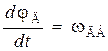, (3.18)

где J = +0,2J_р +J_н/i²;

M'_с.н. = M_с.н./i×h;

w_ДВ = iW_н ;

j_ДВ = ij_н.

Структурная схема исполнительного механизма, построенная по уравнению (3.18), показана на рисунке 3.2.

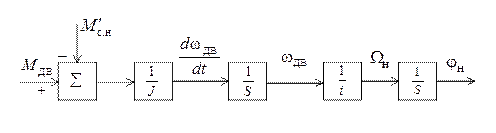
Рисунок 3.2

Однако такая модель исполнительного механизма является идеальной. Она предполагает, что развиваемый двигателем момент отрабатывается абсолютно точно и быстро. В действительности при скачкообразном изменении напряжения U_ДВ на якорной обмотке двигателя момент меняется в лучшем случае по экспоненте. Это объясняется тем, что ротор двигателя и нагрузка на оси его вала инерционны, и он не может мгновенно разогнаться до заданной угловой скорости. Поэтому структурную схему исполнительного механизма строят с учетом динамики исполнительного двигателя.

На рисунке 3.3 показана структурная схема исполнительного механизма, построенного на основе двигателя постоянного тока.

Рисунок 3.3

Для выбранного двигателя параметры схемы могут быть заданы, например Т_Я, или рассчитаны по формулам

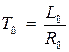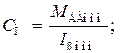
; , (3.19)

где L_Я – индуктивность обмотки якоря;

R_Я – активное сопротивление обмотки;

I_Я – ток, протекающий по обмотке;

U_ДВ – напряжение на обмотке якоря.

Если положить Т_Я = 0, = 0, то на основании структурной схемы для нагруженного двигателя получим передаточную функцию

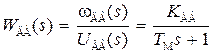, (3.20)

где К_ДВ – коэффициент передачи двигателя по скорости

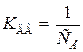; (3.21)

Т_М – механическая постоянная двигателя под нагрузкой

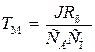. (3.22)

Исследуем динамику двигателя в двух режимах его работы: в режиме разгона до установившейся скорости w₀ и в режиме установившегося движения со скоростью w₀.

Разгон двигателя.

В этом режиме моментом сопротивления можно пренебречь, поскольку его величина значительно меньше величины приведенного момента инерции J, возникающего при ускоренном движении. Преобразуя структурную схему при 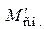= 0, получаем передаточную функцию исполнительного двигателя

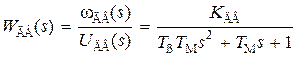. (3.23)

Однако двигатель можно считать колебательным звеном только при выполнении условия 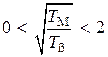. Если 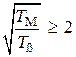, то при таком соотношении постоянных времени передаточная функция (3.23) преобразуется к виду

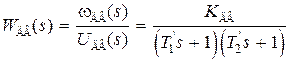, (3.24)

где 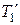и – постоянные времени эквивалентных апериодических звеньев,
которые находят по формуле

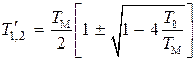. (3.25)

Более того, при 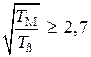можно использовать с погрешностью менее 5 % следующие выражения

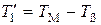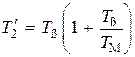; . (3.26)

При 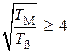влиянием постоянной времени Т_Я на переходные процессы можно пренебречь.

В этом случае 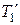= Т_М, а передаточная функция двигателя принимает вид

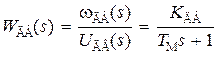. (3.27)

Примерная апериодическая форма изменения угловой скорости двигателя w_ДВ(t) при разгоне для различных значений 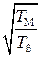показаны на рисунках 3.4 и 3.5

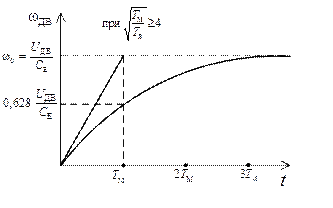
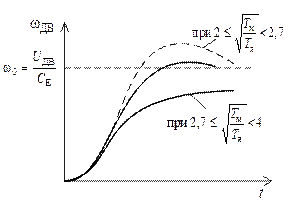
Рисунок 3.4 Рисунок 3.5

Начальная кривизна графиков в области малых значений времени на рисунке 3.5 обусловлена в основном влиянием постоянной времени Т_Я. Перерегулирование при разгоне до номинальной скорости не превышает 5 %. Время разгона можно приближенно оценить по формуле

. (3.28)

При 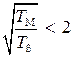разгон носит колебательный характер, примерная форма которого показана на рисунке 3.6.

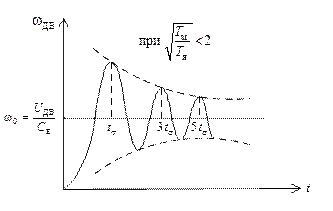
Рисунок 3.6

В этом случае при разгоне угловая скорость достигает больших значений, чем скорость установившегося движения, при этом перерегулирование

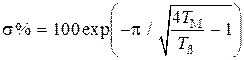, (3.29)

а время разгона можно приближенно оценить по формуле

. (3.30)

Перерегулирование при разгоне является нежелательным явлением. Предотвратить его можно соответствующим управлением в системе.

Установившееся движение.

Исследуем влияние момента сопротивления на движение двигателя с установившейся скоростью w₀, для чего согласно схеме (см. рисунок 3.3) сначала запишем передаточную функцию исполнительного двигателя по возмущению – статическому моменту сопротивления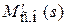

, (3.31)

где 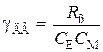– коэффициент наклона механических характеристик двигателя.

Затем запишем выражение для установившегося движения:

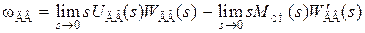. (3.32)

Подставив в выражение (3.32) передаточные функции (3.23), изображения Лапласа напряжения на якорной обмотке двигателя 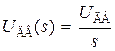и статического момента сопротивления 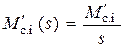и сделав необходимые математические преобразования, получим

, (3.33)

где 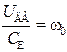– требуемая установившаяся скорость двигателя, а

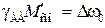– моментная погрешность скорости.

Моментная погрешность, порождаемая реальными условиями применения исполнительного двигателя, искажает его движение, а, следовательно, и движение нагрузки. Снизить погрешность, ослабить чувствительность двигателя к внешним возмущениям удается за счет повышения астатизма системы управления к статическому моменту сопротивления 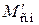; за счет применения в системе специального наблюдающего устройства, по оценкам которого осуществляется компенсация ошибки.

Пример. Технические данные исполнительного двигателя СЛ 521:

U_Д = 110 В; w_{ДВ ном} = 315 рад/с; I_Я=1,07 А; М_{ДВ ном} = 0,245 Н×м;

М_{ДВ max} = 0,637 Н×м; R_Я = 8,5 Ом; L_Я = 0,058 Гн; J_ДВ = 1,67×10^-4 кг×м²;
под нагрузкой J = 3,46×10^-4 кг×м²; 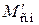= 0,045 Н×м.

Требуется проанализировать динамические свойства двигателя.

Расчет параметров структурной схемы:

– электромагнитная постоянная времени

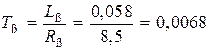с;

– коэффициент момента

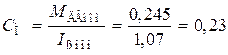Н×м/А;

– коэффициент противо-ЭДС

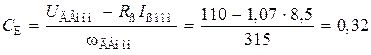В×с/рад;

– жесткость механических характеристик

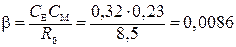Н×м×с/рад;

– механическая постоянная времени двигателя в режиме холостого хода при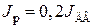

с;

– механическая постоянная времени двигателя под нагрузкой

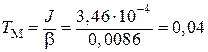с.

Анализ динамики

Соотношение постоянных времени :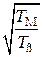

– в режиме холостого хода ;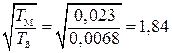

– в режиме движения под нагрузкой .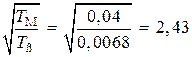

В режиме холостого хода при 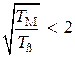разгон описывается затухающей синусоидой с перерегулированием

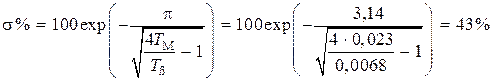
и временем разгона

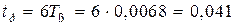с.

В режиме разгона с нагрузкой переходной процесс описывается кривой, представляющей сопряжение двух экспонент, одна из которых соответствует апериодическому звену с постоянной времени 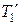, а вторая – апериодическому звену с постоянной времени 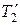, где

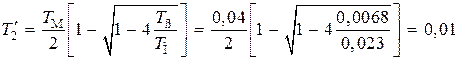с,

с.

Время разгона

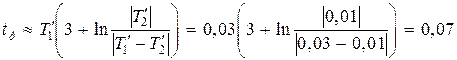с.