Аналоговые регуляторы с отставанием и с опережением по фазе
Регуляторы этого типа находят применение в локальных системах с астатизмом первого порядка. Их передаточная функция имеет вид:
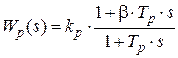 , (4.9)
, (4.9)
где 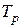 и
и 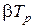 – постоянные времени.
– постоянные времени.
При 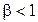 имеем передаточную функцию регулятора с отставанием по фазе, а при
имеем передаточную функцию регулятора с отставанием по фазе, а при 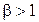 – с опережением по фазе.
– с опережением по фазе.
На рисунках 4.5 и 4.6 показаны асимптотические частотные логарифмические амплитудные характеристики 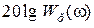 и фазовые характеристики регуляторов при
и фазовые характеристики регуляторов при 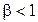 и
и 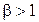 соответственно.
соответственно.
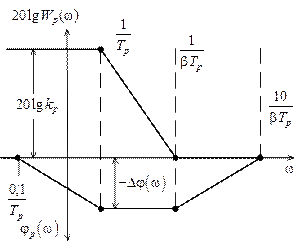 Рисунок 4.5
Рисунок 4.5
| 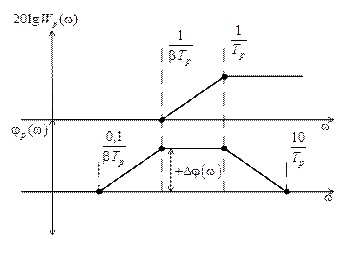 Рисунок 4.6
Рисунок 4.6
|
На рисунке 4.5 видно, что регулятор с запаздыванием ведет себя в области частот 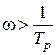 приблизительно так, как ведет себя ПИ-регулятор. Однако вносимый им отрицательный фазовый сигнал будет влиять на фазовую характеристику системы с астатизмом и при неправильном выборе постоянной времени
приблизительно так, как ведет себя ПИ-регулятор. Однако вносимый им отрицательный фазовый сигнал будет влиять на фазовую характеристику системы с астатизмом и при неправильном выборе постоянной времени 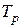 может существенно снизить необходимый запас устойчивости.
может существенно снизить необходимый запас устойчивости.
Регулятор с опережением по фазе, частотные характеристики которого показаны на рисунке 4.6, приблизительно соответствует пропорционально-дифференциальному регулятору (ПД). Регулятор вносит положительный фазовый сдвиг 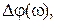 что является благоприятным с точки зрения сохранения необходимого запаса устойчивости по фазе локальной системы. Недостатком регулятора является усиление на высоких частотах, что может приводить к увеличению интенсивности высокочастотных помех и наводок.
что является благоприятным с точки зрения сохранения необходимого запаса устойчивости по фазе локальной системы. Недостатком регулятора является усиление на высоких частотах, что может приводить к увеличению интенсивности высокочастотных помех и наводок.
4.4 Передаточные функции и структурные схемы цифровых
регуляторов
Регуляторы современных локальных систем реализуют на основе микроконтроллеров, контроллеров и микроЭВМ. В этих случаях пропорциональное управление реализуется по-прежнему коэффициента 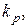 а интегрирование и дифференцирование выполняют в цифровой форме.
а интегрирование и дифференцирование выполняют в цифровой форме.
Существуют различные методы цифровой аппроксимации интегралов и производных их дискретными аналогами. Один из них основан на использовании Z-форм. Например операция интегрирования 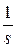 заменяется функцией цифрового интегрирования
заменяется функцией цифрового интегрирования 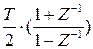 , операция дифференцирования s – функцией цифрового дифференцирования
, операция дифференцирования s – функцией цифрового дифференцирования 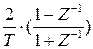 , где
, где 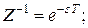 T – период квантования. Используя эти замены в уравнении (4.5), получим цифровую форму передаточной функции ПИД-регулятора:
T – период квантования. Используя эти замены в уравнении (4.5), получим цифровую форму передаточной функции ПИД-регулятора:
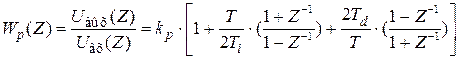 . (4.10)
. (4.10)
Структурная схема цифрового ПИД-регулятора представлена на рисунке 4.7.
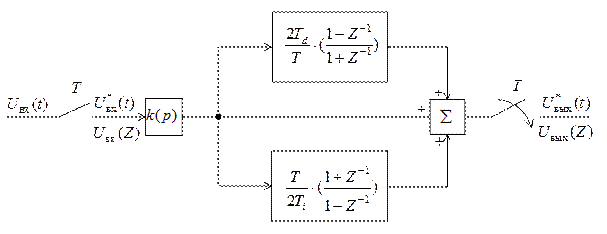
Рисунок 4.7
Цифровой регулятор изображают в виде структурной схемы (рисунок 4.8).
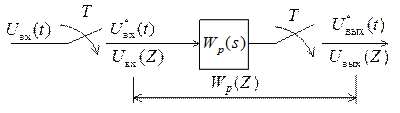
Рисунок 4.8
Входной сигнал регулятора 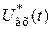 является последовательностью чисел
является последовательностью чисел 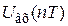 , представляющих собой выборку значений сигнала
, представляющих собой выборку значений сигнала 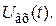 Цифровой регулятор выполняет определенные линейные преобразования последовательности
Цифровой регулятор выполняет определенные линейные преобразования последовательности 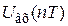 и вырабатывает выходную последовательность
и вырабатывает выходную последовательность 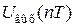 в виде квантового сигнала
в виде квантового сигнала 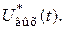
При применении микропроцессорных устройств в качестве регуляторов существуют определенные ограничения, связанные с конечной длинной слова (ошибкой квантования) и с задержкой на время вычисления и дискретизации при выполнении команд в процессоре. Эти факторы оказывают существенное влияние на качество регулирования и устойчивость системы. При высокой частоте дискретизации нет достоверной информации о сигнале 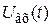 из-за ограниченной разрешающей способности измерительных устройств. Это увеличивает ошибку квантования, и возникает угроза нарушения устойчивости.
из-за ограниченной разрешающей способности измерительных устройств. Это увеличивает ошибку квантования, и возникает угроза нарушения устойчивости.
При низкой частоте дискретизации процессор получает точную информацию о сигнале 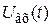 и достаточное время для его обработки. Однако появляется временная задержка, что ведет к снижению запасов устойчивости системы. Оценить период дискретизации крайне сложно. Поэтому рекомендуется определять его наилучшее значение путем моделирования системы, например, в вычислительной среде MATLAB.
и достаточное время для его обработки. Однако появляется временная задержка, что ведет к снижению запасов устойчивости системы. Оценить период дискретизации крайне сложно. Поэтому рекомендуется определять его наилучшее значение путем моделирования системы, например, в вычислительной среде MATLAB.
4.5 Расчет параметров регуляторов непрерывного действия
в одноконтурных системах по критерию качества во временной области
Многие промышленные объекты управления одноконтурных систем описываются передаточной функцией первого порядка с запаздыванием
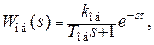 (4.11)
(4.11)
где 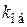 – коэффициент передачи в установившемся режиме;
– коэффициент передачи в установившемся режиме;
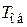 – постоянная времени;
– постоянная времени;
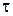 – запаздывание (задержка реакции объекта на единичное ступенчатое
– запаздывание (задержка реакции объекта на единичное ступенчатое
воздействие).
Исполнительные устройства систем содержат жесткую обратную связь по скорости исполнительного двигателя и обратную связь по углу поворота выходного вала редуктора, снижая влияние исполнительного устройства на динамику управляемых процессов. Причем, при постоянной времени двигателя 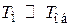 передаточную функцию исполнительного устройства заменяют передаточной функцией безынерционного звена
передаточную функцию исполнительного устройства заменяют передаточной функцией безынерционного звена 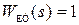 .
.
Располагая значениями параметров объекта управления и практически безынерционным исполнительным устройством, рассчитывают параметры регулятора по формулам, приведенным в таблицах 4.1, 4.2 и 4.3. Таблицу выбирают на основании требований в форме ограничений на время регулирования, величину перерегулирования, степень затухания переходного процесса, чувствительность переходной функции к изменению отношения 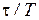 и др.
и др.
Таблица 4.1 – Параметры регуляторов для системы с минимальным временем
регулирования при отсутствии перерегулирования
| Тип регулятора | Kp | Ti | Td |
| П | 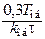
| ||
| ПИ | 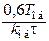
| 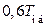
| |
| ПИД | 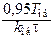
| 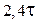
| 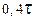
|
Таблица 4.2 – Параметры регуляторов для системы с минимальным временем
первого полупериода затухающих колебаний при 20%-ном
перерегулировании
| Тип регулятора | kp | Ti | Td |
| П | 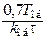
| ||
| ПИ | 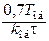
| 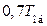
| |
| ПИД | 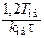
| 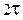
| 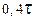
|
Таблица 4.3 – Параметры регуляторов по минимуму чувствительности
переходной функции системы к изменению отношения 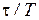
при (10…20)%-ном перерегулировании
| Тип регулятора | kp | Ti | Td |
| П | 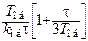
| ||
| ПИ | 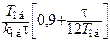
| 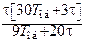
| |
| ПИД | 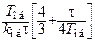
| 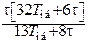
| 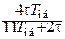
|
Тип регулятора из таблицы выбирают ориентируясь на величину отношения запаздывания 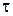 к постоянной времени объекта Тоб. При (
к постоянной времени объекта Тоб. При ( 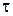 /Тоб) < 0,2 рекомендуется выбирать пропорциональный П-регулятор, при 0,2 ≤ (
/Тоб) < 0,2 рекомендуется выбирать пропорциональный П-регулятор, при 0,2 ≤ ( 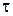 /Тоб) < 1 – ПИ– или ПИД-регулятор, а при (
/Тоб) < 1 – ПИ– или ПИД-регулятор, а при ( 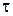 /Тоб) ≥ 1 – специальный ПИД-регулятор с блоками для предсказания будущего поведения объекта управления.
/Тоб) ≥ 1 – специальный ПИД-регулятор с блоками для предсказания будущего поведения объекта управления.
Значения параметров регулятора, полученные по приведенным в таблицах формулам, следует рассматривать как отправные. Используя simulink, их необходимо уточнить с учетом особенностей реализации локальной системы.
Пример. Объект с запаздыванием описывается передаточной функцией (4.11). Параметры передаточной функции имеют следующие значения: Тоб = 300 с; kоб = 0,32; 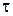 =125 с. Определите желаемую передаточную функцию регулятора, обеспечивающего минимальное время первого полупериода затухающих колебаний при 20 %-м перерегулировании.
=125 с. Определите желаемую передаточную функцию регулятора, обеспечивающего минимальное время первого полупериода затухающих колебаний при 20 %-м перерегулировании.
Расчет.
Для отношения ( 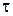 /Тоб) = (129/300) = 0,43 и условия 0,2 <
/Тоб) = (129/300) = 0,43 и условия 0,2 < 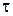 /Тоб < 1 выбираем ПИ-регулятор. Параметры регулятора находим по формулам таблицы 4.2:
/Тоб < 1 выбираем ПИ-регулятор. Параметры регулятора находим по формулам таблицы 4.2:
– коэффициент передачи 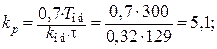
– постоянная интегрирования 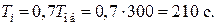
При расчете параметров регулятора предполагалось, что передаточная функция объекта с запаздыванием точно известна. Однако в лучшем случае она известна с точностью до параметров, которые могут отличаться от реальных значений. В частности представляет интерес исследовать реакцию системы на единичное ступенчатое воздействие для постоянных (расчетных) значений параметров регулятора и различных отношений 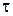 /Тоб из диапазона значений [0,2…0,8] для объекта.
/Тоб из диапазона значений [0,2…0,8] для объекта.
Для удобства определения реакции системы с помощью simulink введем безразмерное время t*= 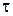 t, т. е. сжимаем время решения задачи. При этом в передаточных функциях регулятора и объекта осуществляем подстановку:
t, т. е. сжимаем время решения задачи. При этом в передаточных функциях регулятора и объекта осуществляем подстановку: 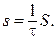 В этом случае передаточная функция разомкнутой системы
В этом случае передаточная функция разомкнутой системы
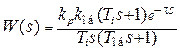 (4.12)
(4.12)
принимает вид
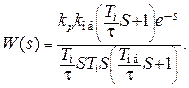 (4.13)
(4.13)
Подставим в выражение (4.13) значение параметра 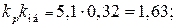
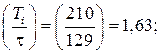
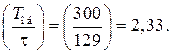
Кроме того, воспользуемся разложением
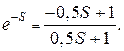 (4.14)
(4.14)
В результате получим передаточную функцию модели разомкнутой системы
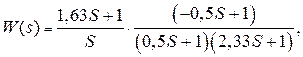 (4.15)
(4.15)
которую удобно использовать при компьютерном исследовании системы замкнутой единичной отрицательной обратной связью.
4.6 Расчет регуляторов одноконтурных системах по критериям
качества в частотной области
Расчет связан с решением следующих задач: синтезом желаемой передаточной функции разомкнутой системы на основе свойств системы в частотной области; определением передаточной функции регулятора; реализацией регулятора с учетом реальных условий его применения; проверкой показателей качества переходного процесса.
Решение задач получим для систем, которые в разомкнутом состоянии без регулятора (Wр(s) = 1) имеют передаточную функцию
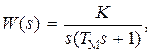 (4.16)
(4.16)
где К – общий коэффициент усиления системы в разомкнутом состоянии.
Хотя передаточная функция имеет простой вид, тем не менее, она часто встречается в системах, осуществляющих механическое движение рабочих органов объектов необходимое для выполнения рабочего процесса. Выходной координатой этих систем является угол поворота выходного вала системы, а входной, определяющей требуемое значение угла выходного вала, может быть угол поворота задатчика, напряжение, управляющая программа и т. д.
Характерной особенностью систем является их подверженность возмущениям, возникающим в процессе выполнения механических движений и нарушающим управление этими движениями.
Синтез желаемой передаточной функции разомкнутой локальной системы. На начальном этапе синтеза желаемую передаточную функцию Wж(s) выбирают по виду передаточной функции W(s) разомкнутой нескорректированной системы, состоящей из функционально необходимых элементов, например в соответствии с передаточной функцией (4.16) выбирают передаточную функцию
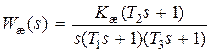 , (4.17)
, (4.17)
где Кж, Т1, Т2, Т3 – желаемые значения общего коэффициента усиления разомкнутой системы и постоянных времени, удовлетворяющие требованиям устойчивости, точности установившихся режимов работы к качеству переходных процессов.
Параметры желаемой передаточной функции (4.17) рассчитывают обычно по методике В. А. Бесекерского, используя в качестве исходных следующие данные:
− максимальное установившееся значение статического момента сопротивления нагрузки, приведенного к валу исполнительного двигателя 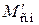 ;
;
− максимальная угловая скорость нагрузки Wmax;
− максимальное угловое ускорение нагрузки emax;
− допустимое установившееся значение ошибки dmax при движении с постоянной скоростью, равной Wmax, и статическом моменте МС.Н;
− коэффициент наклона механических характеристик двигателя с редуктором g0 = gДi-1;
− показатель колебательности М.
Расчет можно упростить, если с помощью приведенных ниже формул определить величины, характеризующие частотные свойства системы
–контрольная частота
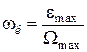 ; (4.18)
; (4.18)
− добротность системы по скорости
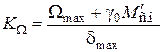 ; (4.19)
; (4.19)
– условная добротность системы по ускорению
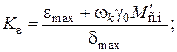 (4.20)
(4.20)
– базовая частота
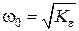 . (4.21)
. (4.21)
Расчет параметров. Расчет общего коэффициента усиления Кж и первой наибольшей постоянной времени Т1 можно осуществить различным образом.
Вариант первый. Выбираем
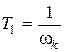 . (4.22)
. (4.22)
Тогда требуемое значение коэффициента Кж должно удовлетворять условию
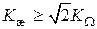 . (4.23)
. (4.23)
При этом базовая частота w0 принимает значение
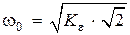 . (4.24)
. (4.24)
Вариант второй. Выбираем
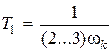 . (4.25)
. (4.25)
В этом случае желаемый коэффициент усиления разомкнутой системы или добротность по скорости имеет минимально возможное значение
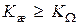 , (4.26)
, (4.26)
что благоприятно сказывается на помехозащищенности системы. Однако при этом возрастает условная добротность по ускорению
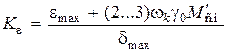 , (4.27)
, (4.27)
а следовательно, и базовая частота
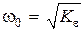 , (4.28)
, (4.28)
что приводит к сложному алгоритму работы регулятора.
Вариант третий. Выбираем
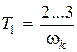 . (4.29)
. (4.29)
При этом условная добротность по ускорению будет минимальной
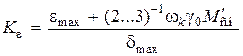 . (4.30)
. (4.30)
Минимальную величину принимает и базовая частота 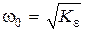 , что благоприятно сказывается на реализации алгоритма работы регулятора. В то же время общий желаемый коэффициент усиления разомкнутой системы возрастает в два-три раза по сравнению с минимальным значением, равным КW:
, что благоприятно сказывается на реализации алгоритма работы регулятора. В то же время общий желаемый коэффициент усиления разомкнутой системы возрастает в два-три раза по сравнению с минимальным значением, равным КW:
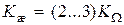 . (4.31)
. (4.31)
Увеличение Кж может быть нежелательным при работе системы в условиях помех на входе системы или действующих внутри системы.
Для любого варианта постоянные времени Т2 и Т3 рассчитывают по следующим формулам
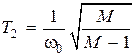 ; (4.32)
; (4.32)
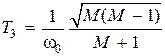 . (4.33)
. (4.33)
Отношение постоянных времени
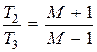 (4.34)
(4.34)
характеризует запасы устойчивости системы и перерегулирование в переходных режимах работы. Обычно это отношение должно лежать в пределах [6…12].
Пример. Рассчитать параметры желаемой передаточной функции (4.17) по следующим исходным данным:
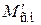 = 0,2 Н×м; Wmax = 0,32 рад/с; emax = 0,27 рад/с2; g0 = 0,4 рад/нмс; М = 1,26; dmax = 8 угловых минут.
= 0,2 Н×м; Wmax = 0,32 рад/с; emax = 0,27 рад/с2; g0 = 0,4 рад/нмс; М = 1,26; dmax = 8 угловых минут.
Расчет.
Контрольная частота
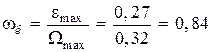 с–1.
с–1.
Добротность системы по скорости
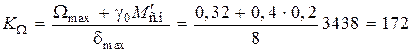 с–1.
с–1.
Условная добротность системы по ускорению
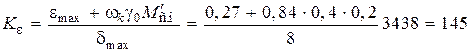 с–1.
с–1.
Базовая частота 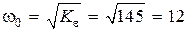 с–1.
с–1.
Дальнейший расчет проводим для следующих двух вариантов общего коэффициента Кж и наибольшей постоянной времени Т1.
Вариант первый. Пусть 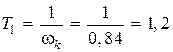 с.
с.
Тогда 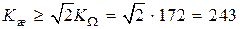 с–1. Принимаем
с–1. Принимаем 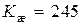 с–1.
с–1.
Находим базовую частоту 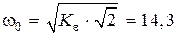 с–1.
с–1.
Постоянные времени
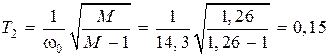 с;
с;
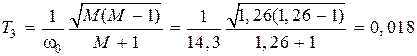 с.
с.
Желаемая передаточная функция
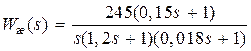 .
.
Вариант второй. Пусть постоянная времени 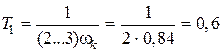 с.
с.
Тогда 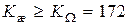 с-1. Принимаем
с-1. Принимаем 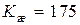 с–1.
с–1.
Постоянные времени при 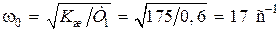
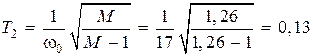 с;
с;
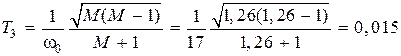 с.
с.
Желаемая передаточная функция
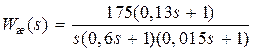 .
.
Расчет регуляторов. Задача состоит в том, чтобы не только усилить сигнал ошибки регулирования Ud, но и придать системе желаемые динамические свойства Wж(s). Это означает, что регулятор должен обладать передаточной функцией вида
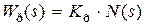 , (4.35)
, (4.35)
где Kр – коэффициент преобразования (усиления) регулятора;
N(s) – дробно-рациональная физически реализуемая функция.
Коэффициент преобразования Kр можно определить из условия K = Kж, подставив в него значение K = KД Kр KП KДВ i–1:
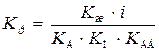 , (4.36)
, (4.36)
Функцию N(s) получают путем деления желаемой передаточной функции Wж(s) на передаточную функцию исходной системы W(s) при K = Kж:
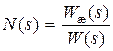 . (4.37)
. (4.37)
Подставив в формулу (4.37) выражения (4.16) и (4.17), получим
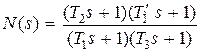 , (4.38)
, (4.38)
где знак (') означает, что постоянная времени 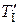 является постоянной времени регулятора и, вообще говоря, должна быть численно равна электромеханической постоянной времени исполнительного двигателя Тм.
является постоянной времени регулятора и, вообще говоря, должна быть численно равна электромеханической постоянной времени исполнительного двигателя Тм.
Физическая реализуемость функции N(s) с помощью RC-фильтров. Реализация функции N(s) в виде электрического четырехполюсника, расположенного перед управляемым силовым преобразователем, показана на рисунке 4.9.
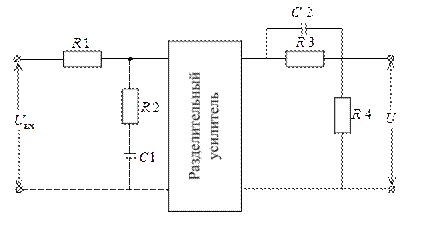
Рисунок 4.9
Фильтр на входе разделительного усилителя описывается передаточной функцией
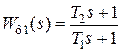 , (4.39)
, (4.39)
где
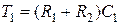 ;
; 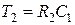 . (4.40)
. (4.40)
Передаточная функция фильтра, подключенного к выходу разделительного усилителя, имеет вид
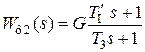 , (4.41)
, (4.41)
где
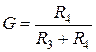 ;
; 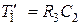 ;
; 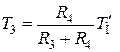 . (4.42)
. (4.42)
Видно, что второй фильтр ослабляет сигнал в G раз. Чтобы скомпенсировать это ослабление, разделительный усилитель должен обеспечивать усиление, равное 1/G.
Реализация с помощью ПИД-регулятора. Передаточную функцию (4.38) преобразуем к следующему виду
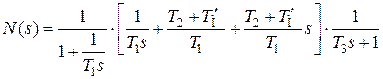 . (4.43)
. (4.43)
Выражение, заключенное в квадратные скобки, представляет собой передаточную функцию классического ПИД–регулятора.
Дифференцирующее звено 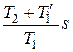 в выражении (4.43) обычно реализуют совместно с фильтром верхних частот. Передаточная функция физически реализуемого дифференцирующего звена имеет вид
в выражении (4.43) обычно реализуют совместно с фильтром верхних частот. Передаточная функция физически реализуемого дифференцирующего звена имеет вид
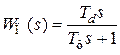 , (4.44)
, (4.44)
где 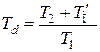 , а постоянную времени Тф выбирают так, чтобы можно было пренебречь влиянием фильтра на запасы устойчивости и динамику системы. Обычно Тф выбирают из условия Тф ≤ (0,1…0,15)Т3.
, а постоянную времени Тф выбирают так, чтобы можно было пренебречь влиянием фильтра на запасы устойчивости и динамику системы. Обычно Тф выбирают из условия Тф ≤ (0,1…0,15)Т3.
Зная Тd и Тф, можно вычислить отношение постоянных времени
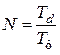 , (4.45)
, (4.45)
а передаточную функцию (4.44) представить в следующем виде
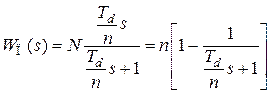 . (4.46)
. (4.46)
Тогда выражение (4.43) при стандартных обозначениях Т1 = Тi; 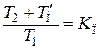 с учетом (4.46) принимает вид
с учетом (4.46) принимает вид
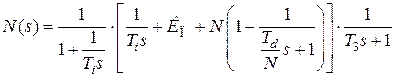 . (4.47)
. (4.47)
Структурная схема физически реализуемого ПИД-регулятора, построенная в соответствии с выражением (4.47), показана на рисунке 4.10.
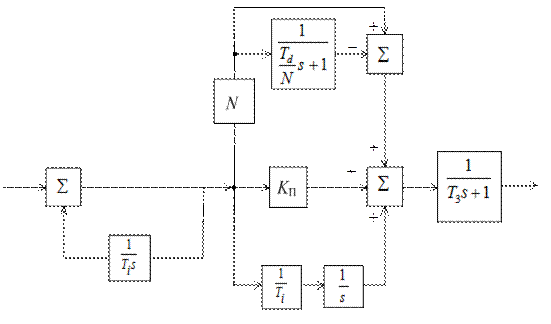
Рисунок 4.10
Расчет регуляторов в двухконтурной системе. Структурная схема системы показана на рисунке 1.2. Внутренний контур с регулятором Р2 в цепи местной обратной связи позволяет упростить передаточную функцию (4.37) регулятора Р1 в прямой цепи управления.
Действительно, анализ параметров желаемой передаточной функции (4.17) показывает, что постоянная времени Т1 и Т2 определяются только параметрами движения нагрузки и требованиями к показателю колебательности системы и никак не зависят от параметров исполнительного устройства. Поэтому для прямого управления подходящим является регулятор Р1 с отставанием по фазе
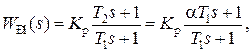
где 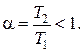
Вид передаточной функции регулятора Р2 в цепи обратной связи осуществляется следующим образом. Если в исполнительном устройстве обратной связью охватывают силовой преобразователь и двигатель, имеющие передаточную функцию
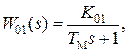
где K01 = KПKДВ, то в цепи обратной связи выбирают регулятор пропорционального действия с передаточной функцией
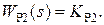
В этом случае результирующая передаточная функция контура определяется выражением
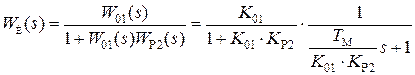 (4.48)
(4.48)
или
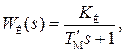 (4.49)
(4.49)
где новые параметры имеют вид
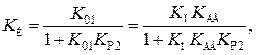 (4.50)
(4.50)
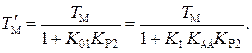 (4.51)
(4.51)
Для расчета коэффициента KР2 целесообразно в формуле (4.51) положить 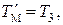 что эквивалентно сокращению нуля и полюса в передаточной функции (4.38). Тогда получим
что эквивалентно сокращению нуля и полюса в передаточной функции (4.38). Тогда получим
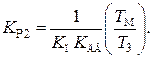 (4.52)
(4.52)
Из формулы (4.50) следует, что регулятор обратной связи пропорционального действия в (1 + KПKДВ KР2) уменьшает коэффициент передачи исполнительного устройства. Поэтому во столько раз необходимо увеличить коэффициент передачи регулятора Р1 в прямой цепи управления.
Функции регулятора обратной связи пропорционального действия обычно реализуют на базе техогенератора с делителем напряжения, как показано на рисунке 4.11.
В том случае, когда охватываемая обратной связью функциональная часть исполнительного устройства имеет передаточную функцию
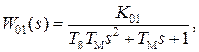 (4.53)
(4.53)
рекомендуется в цепи обратной связи использовать регулятор с опережением по фазе
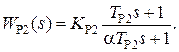 (4.54)
(4.54)
Параметры регулятора рассчитывают по следующим формулам:
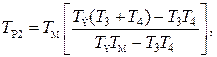 (4.55)
(4.55)
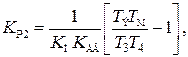 (4.56)
(4.56)
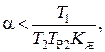 (4.57)
(4.57)
где Т1, Т2, Т3, Т4 и KЖ являются параметрами желаемой передаточной функции.
На рисунке 4.12 показана схема, реализующая функции регулятора с опережением по фазе.
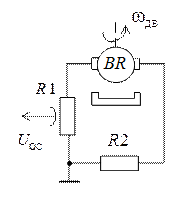
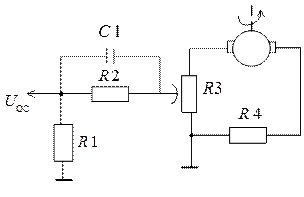
Рисунок 4.11 Рисунок 4.12
Выше при выборе регуляторов и расчете их параметров предполагалось, что локальная система обладает достаточным запасом устойчивости и точностью регулирования в условиях постоянного действующего момента сопротивления нагрузки. При этом погрешность, вносимая моментом сопротивления, не превышает заданного значения. Однако двухконтурные системы в установившемся режиме работы позволяют свести эту погрешность к нулю. Необходимо лишь перестроить структурную схему системы. Один из вариантов схемы показан на рисунке 4.13, где Kд.с – передаточный коэффициент датчика скорости.
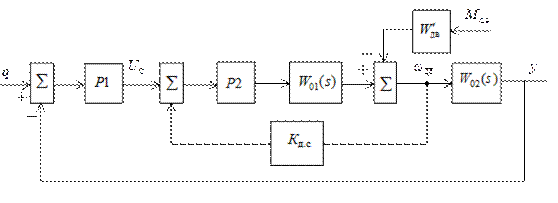
Рисунок 4.13
Пусть 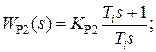
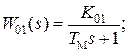
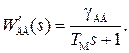 Выбираем
Выбираем 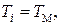 тогда передаточная функция внутреннего контура по возмущению МС.Н принимает вид
тогда передаточная функция внутреннего контура по возмущению МС.Н принимает вид
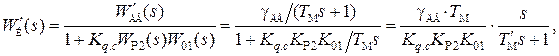 (4.58)
(4.58)
где новая постоянная времени
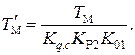
Появление оператора s в числителе передаточной функции (4.58) указывает на то, что система обладает астатизмом первого порядка по отношению к внешним возмущения. Постоянные во времени внешние моменты М¢с.н не сказываются на точности отработки заданного задающего воздействия в установившемся режиме.
Вопросы для проверки усвоения материала
1 Поясните назначение регулятора в локальных системах автоматики.
2 Поясните назначение пропорциональной, интегральной и дифференциальной составляющей в ПИД-регуляторе.
3 Как влияет интегральная составляющая ПИ и ПИД-регулятора на качество переходных процессов в локальных системах?
4 В каких случаях находят применение регуляторы с отставанием и с опережением по фазе?
5 Из каких соображений выбирают закон регулирования промышленных объектов первого порядка с запаздыванием по критериям во временной области?
6 Приведите методику расчета регуляторов одноконтурных систем по критериям в частотной области.
Заключение
Пособие охватывает наиболее важные вопросы проектирования локальных систем автоматики.
Основное внимание уделяется выбору элементов и расчету их статических и динамических характеристик, обеспечивающих требуемое качество системы и с которых, как правило, начинается проектирование. При этом подчеркивается необходимость учета конечной точности измерительных устройств, чувствительности исполнительного механизма к внешним возмущениям, естественных ограничений на переменные состояния системы в переходных режимах, запаздывания реакции объекта на управляющие воздействия.
Рассмотрены формы регуляторов и методы расчета их параметров. Эти методы до сих пор остаются основными, несмотря на множество других методов, имеющих преимущества для систем конкретного применения.
Надеемся, что весьма сжатые сведения в учебном пособии являются достаточными для того, чтобы без затруднений перейти к более глубокому изучению соответствующих тем в опубликованных источниках, например, перечисленных ниже в списке литературы.
Пособие может быть использовано для индивидуального изучения и самостоятельного выполнения задания по курсовому проекту. В то же время оно будет полезно для преподавания различных курсов в области автоматизации.
Список литературы
1 Солодовников, В. В. Основы теории и элементы систем автоматичес-кого регулирования / В. В. Солодовников, В. Н. Плотников, А. М. Яковлев. – М. : Машиностроение, 1985.
2 Основы проектирования следящих систем / под ред. Н. А. Лакоты. – М. : Машиностроение, 1978.
3 Гудвин, Г. К. Проектирование систем управления / Г. К. Гудвин, С. Ф. Гребе, М. Э. Сальгадо. – М. : БИНОМ. Лаборатория знаний, 2004.
4 Дорф, Р. Современные системы управления / Р. Дорф, Р. Бишоп; пер. с англ. Б. И. Копылова. – М. : Лаборатория Базовых Знаний, 2002.
5 Герман-Галкин, С. Г. Matlab & Simulink: Проектирование мехатронных систем на ПК / С. Г. Герман-Галкин. – М. : Корона-Век, 2008.
6 Терехов, В. М. Системы управления электроприводов / В. М. Терехов, О. И. Осипов. – М. : Академия, 2005.
7 Белов, М. П. Автоматизированный электропривод типовых произ-водственных механизмов и технологических комплексов : учебник для вузов / М. П. Белов, В. А. Новиков, Л. Н. Рассудов. – М. : Академия, 2004.
8 Козярук, А. Е. Современное и перспективное алгоритмическое обеспе-чение частотно-регулируемых электроприводов / А. Е. Козярук, В. В. Рудаков, А. Г. Народицкий. – СПб. : СПЭК, 2004.
9 Клевцов, А. В. Преобразователи частоты для электроприводов переменного тока / А. В. Клевцов. – Тула : График и к, 2008.
10 Системы программного управления промышленными установками и робототехническими комплексами / Б. Г. Коровин [и др.]. – Л. : Энергоатом-издат, 1990.
11 Руководство по проектированию систем автоматического управления / под ред. В. А. Бесекерского. – М. : Высш. шк., 1984.
12 Красовский, А. Я. Расчет многоконтурных систем управления электро-приводами / А. Я. Красовский, М. К. Хаджинов. – Минск : БГУИР, 1996.
Дата добавления: 2020-06-09; просмотров: 919;











