Выполнимыми являются выражения, которые по меньшей мере при одном сочетании значений своих пропозициональных переменных принимают значение «истина».
С учетом объединения нейтральных выражений и законов в одну разновидность все формулы логики высказываний подразделяются на два класса - выполнимые и противоречия.
Среди законов логики высказываний имеются фундаментальные, из которых выводятся менее общие, производные от них. Таким образом, вся теория символической логики может быть развернута в длинную цепь теорем и положений. Самые первые установления задаются аксиоматически - постулируются без доказательства. Выработка аксиом, удовлетворяющих всем требованиям к ним целиком и полностью, - не такая уж простая задача. Существует несколько возможных вариантов аксиоматического построения символической логики, в основу которых кладутся разные наборы простых и достаточно самоочевидных положений, называемых иногда тавтологиями. В этом учебнике не предусматривается теоретически строгое выведение всей совокупности законов символической логики, так как это предполагает серьезную математическую подготовку.
Мы остановимся лишь на самых важных и наиболее применимых на практике[Остальное в этом параграфе можно не изучать, если возникнут трудности.]. Совокупность развитых ранее положений послужит нам теоретической базой, они помогут нам обосновать последующие установления символической логики. В этом смысле те принципы, которые уже рассмотрены, являются фундаментальными, они позволят нам вывести последующие. Но надо помнить, что их математически строгого обоснования здесь нет. Развернутая на предыдущих страницах аргументация построена отчасти на примерах, отчасти на полуинтуитивных догадках. Однако поскольку в гуманитарных отраслях науки большей строгости и не требуется, то с точки зрения принятых здесь критериев достигаемое таким путем теоретическое единство более чем удовлетворительно решает основную задачу - придать изложению предельно компактный характер.
Ряд положений в логике называют правилами. Они тоже могут быть записаны формулами, но используются в первую очередь при выполнении операций.
Правило подстановки.Исключительно большую роль в преобразованиях символических выражений играет правило подстановки. Мы уже пользовались им, хотя не давали обоснования этому. Согласно данному правилу любую буквенную переменную в символическом выражении можно заменять на произвольную формулу. Если исходная формула - общезначимое выражение, то тогда и новая усложненная формула тоже будет общезначимой. Так, в законе исключенного третьего 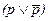 вместо p можно вставить, скажем,
вместо p можно вставить, скажем, 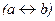 и тогда получится выражение
и тогда получится выражение 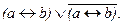
Читаться оно теперь уже будет так: или верно, что 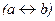 , или неверно, что
, или неверно, что 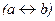 . Понятно само собой, что это выражение останется общезначимым. Замена же переменных формулами в нейтральных выражениях может приводить к изменению истинностных значений некоторых наборов переменных.
. Понятно само собой, что это выражение останется общезначимым. Замена же переменных формулами в нейтральных выражениях может приводить к изменению истинностных значений некоторых наборов переменных.
Наряду с развертыванием формул в более сложные правило подстановки позволяет также делать обратные преобразования - свертывать большие формулы в более сжатые, когда в них попадаются повторяющиеся элементы. Например, в формуле
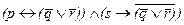
дважды встречается выражение 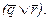 Обозначив этот элемент через t, можно записать исходную формулу компактнее:
Обозначив этот элемент через t, можно записать исходную формулу компактнее:
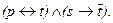
Правило дистрибутивности. Еще одним важным установлением логики высказываний является так называемое правило дистрибутивности, которое записывается в двух выражениях:
AÙ(BÚC)=(AÙB)Ú(AÙC), (10)
AÚ(BÙC)=(AÚB)Ù(AÚC). (11)
Это правило можно записать для большего числа переменных, если воспользоваться правилом подстановки. Допустим, у нас имеется формула (AÚB)Ù(CÚD). Заменим одну из скобок, скажем первую, буквой E и тогда у нас получится выражение, для которого закон дистрибутивности уже написан нами: EÙ(CÚD), Это позволит нам записать новое выражение
(AÚB)Ù(CÚD)= EÙ(CÚD),
применив к нему правило (10), получим
(AÚB)Ù(CÚD)= (EÙC)Ú (EÙD).
Теперь снова воспользуемся правилом подстановки, но уже для обратной цели - развернуть каждую из стоящих справа скобок и затем применить к каждой из них правило (10):
(AÚB)Ù(CÚD)= ((AÚB)ÙC)Ú ((AÚB)ÙD),
(AÚB)Ù(CÚD)= ((AÙC)Ú (BÙC)Ú (AÙD)Ú (BÙD)).
В последнем преобразовании мы учли также правило, разрешающее переставлять местами конъюнкты. Наконец, убрав лишние скобки и записав дизъюнкты в другом порядке, получим усложненное правило дистрибутивности:
(AÚB)Ù(CÚD)= ((AÙC)Ú (AÙD) Ú (BÙC) Ú (BÙD)). (12)
Совершенно аналогично можно и правило дистрибутивности (11) обобщить на большее число переменных:
(AÙB)Ú(CÙD)= ((AÚC)Ù(AÚD)Ù(BÚC)Ù(BÚD)). (13)
Закон двойственности. В логике высказываний имеется также закон двойственности. Из формул (2) и (4) можно увидеть, что конъюнкция и дизъюнкция переходят друг в друга в некотором отношении подобным образом: чтобы получить из дизъюнкции конъюнктивное выражение, надо поменять знаки над пропозициональными переменными и над самой формулой, затем поменять знак дизъюнкции на конъюнктивный. Точно таким же образом конъюнкция переходит в дизъюнкцию. В логике высказываний доказывается также, что сходным способом преобразуются строгая дизъюнкция и эквивалентность:
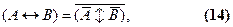
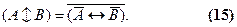
Мы можем получить эту формулу, опираясь на те фундаментальные положения, которые изучены ранее. Для этого надо осуществить цепочку эквивалентных преобразований выражения (A«B). Сначала согласно (8) заменить эквивалентность на конъюнкцию двух импликаций и одновременно перевести импликации в дизъюнкции согласно (7), затем с помощью правила дистрибутивности для четырех переменных (12) развернуть формулу
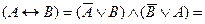
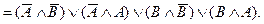
Освобождаем полученное выражение от тождественно-ложных дизъюнктов и получаем
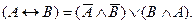
Две образовавшиеся у нас конъюнкции переведем в дизъюнкции (равносильность (2)):
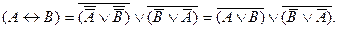
И теперь полученную дизъюнкцию двух скобок переведем в соответствии с (4) в конъюнкцию тех же скобок:
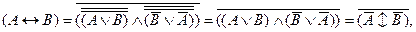
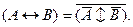
После упрощений нами получено выражение, в котором нетрудно узнать отрицание строгой дизъюнкции, записанной через эквивалентность (9), свернув ее в соответствии с этой формулой, мы получили формулу, которую надо было доказать.
Заметим попутно, что строгая дизъюнкция при одновременной смене знаков над обоими ее переменными не меняет своего семантического значения; это можно увидеть из закона (9): при подобной смене все сводится к перестановке правой и левой скобок.
Обоснование второй из приведенных формул проводится аналогично.
Знаки Ù и Ú, а также 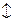 и « называют двойственными. И все формулы, получающиеся простой заменой знаков на двойственные им, тоже называют двойственными. Переход в двойственное выражение, описываемый законами (2), (4), (14), (15), осуществляется и применительно к двойственным формулам любой сложности. Так, если у нас имеется формула
и « называют двойственными. И все формулы, получающиеся простой заменой знаков на двойственные им, тоже называют двойственными. Переход в двойственное выражение, описываемый законами (2), (4), (14), (15), осуществляется и применительно к двойственным формулам любой сложности. Так, если у нас имеется формула
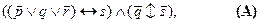
то двойственная ей будет
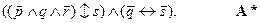
Как гласит закон двойственности, если формулы A и B эквивалентны, то тогда обязательно эквивалентны между собой и двойственные им формулы A* и B*.
В том случае, когда формула содержит знаки импликации и отрицания над выражениями, то для образования двойственной ей надо сначала избавиться от того и другого, после этого можно строить двойственную формулу.
С помощью принципа двойственности легко осуществлять отрицание любого выражения. Для этого надо заменить все знаки над переменными на противоположные, а все логические союзы - на двойственные (избавив, разумеется, сначала формулу от импликации и отрицаний над скобками, если они там имеются).
Закон контрапозиции. Этот закон был известен еще Аристотелю. В традиционной логике с ним приходится сталкиваться в разделе о непосредственных умозаключениях и среди условно-категорических силлогизмов. Суть этого закона состоит в том, что, когда нам известна обусловленность одного положения другим (A®B) , то отсутствие второго является свидетельством отсутствия первого (от отсутствия следствия можно заключать к отсутствию основания - 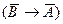 . Существует закон простой контрапозиции и сложной. Простой вариант этого закона может быть записан следующим образом:
. Существует закон простой контрапозиции и сложной. Простой вариант этого закона может быть записан следующим образом:
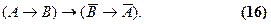
Покажем, что эта формула является тождественно-истинной. Для этого преобразуем все импликации в дизъюнкции, воспользовавшись соответствующими формулами:
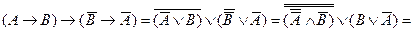
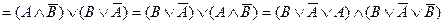 .
.
На последнем этапе преобразований мы воспользовались правилом дистрибутивности, причем скобка 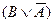 выполняла роль одного из членов выражения для этого правила. Получилась конъюнктивная нормальная форма; ее каждая элементарная дизъюнкция содержит переменную вместе со своим отрицанием, следовательно, исходное выражение является тождественно-истинным или законом..
выполняла роль одного из членов выражения для этого правила. Получилась конъюнктивная нормальная форма; ее каждая элементарная дизъюнкция содержит переменную вместе со своим отрицанием, следовательно, исходное выражение является тождественно-истинным или законом..
Можно обосновать и более сильное выражение этого же самого закона простой контрапозиции. Для этого надо сначала применить полученный закон к выражению 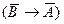 :
:
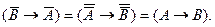
А это означает, что закон контрапозиции действует как в прямом, так и в обратном порядке, и мы можем написать его в двух формах:
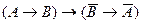 ,
, 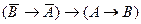 ,
,
затем конъюнктивно объединить обе формулы в одну:
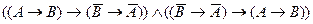
и потом заменить обе импликации (в больших скобках) на одну эквивалентность, как это допускается формулой (8). Тогда у нас между скобками в (16) будет стоять не знак импликации, а эквивалентность:
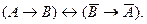
В традиционной логике некоторым подобием контрапозиции является противопоставление предикату. Согласно правилам этого вида непосредственного умозаключения из суждения, скажем, «Радуга имеет семь цветов» можно вывести: «Несемицветное не является радугой». Чтобы сходство с контрапозицией стало очевиднее, лучше записать все рассуждение в иной форме: «Если явление есть радуга, то оно семицветное; следовательно, если явление не семицветное, то оно не есть радуга» 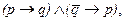 где p - «Явление есть радуга», q - «Явление - семицветное»).
где p - «Явление есть радуга», q - «Явление - семицветное»).
Обратите, однако, внимание, что в традиционной логике обратное преобразование сделать нельзя. То есть, взяв конец нашего рассуждения («Если явление не семицветное, то тогда оно - не радуга») и преобразовав его по правилам противопоставления предикату, мы получим вместо того суждения, с которого начали («Радуга имеет семь цветов»), существенно иное: «Некоторые явления, не являющиеся радугой, имеют семь цветов». В силу этих обстоятельств правильнее считать законом простой контрапозиции формулу (16), а не более сильный вариант. Его обоснование оказалось возможным из-за действующих в символической логике упрощающих допущений, о чем уже неоднократно говорилось.
Закон усложненной контрапозиции. Преимущество методов символической логики над традиционными в данном вопросе состоит в том, что они позволяют усложнить закон контрапозиции, распространив его на выражения с тремя переменными.
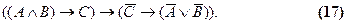
Его интерпретацией может быть, скажем, такое рассуждение: «Если абитуриент сдал вступительные экзамены и оплатил обучение, то он зачисляется в вуз, следовательно, если он не зачисляется в вуз, то значит или не сдал вступительные экзамены, или не оплатил обучение».
Как и в первом случае, мы подтвердим с помощью КНФ общезначимость этой формулы. Для этого заменим все импликации в формуле на дизъюнкции в согласии с (7):
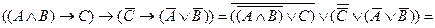
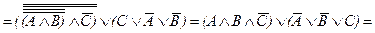
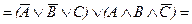
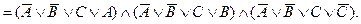
Полученная КНФ показывает, что данная формула общезначима. Как и в случае простой контрапозиции, можно точно так же доказать и более сильное выражение этого закона, когда между двумя половинками формулы не импликация, и эквивалентность.
Закон импортации. Его называют также законом внесения антецедента и записывают с помощью формулы
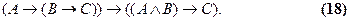
Смысл этого выражения не нуждается в особом пояснении. «Если зимой наступает оттепель, то, если затем ударит мороз, тогда на улицах гололед, отсюда следует, что если зимой наступает оттепель и затем ударит мороз, то тогда на улицах гололед» - такой пример может послужить иллюстрацией этого закона. Его приведение к конъюнктивной нормальной форме тоже не представляет особых затруднений:
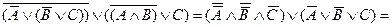
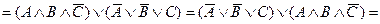
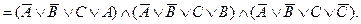
Первое выражение получилось в результате замен всех импликаций в соответствии с (7) на дизъюнкции, затем мы стали преобразовывать конъюнкции в соответствии с (2) и дизъюнкции по формуле (4). Из полученного итога непосредственно виден общезначимый характер исходной формулы (18).
Закон экспортации. Этот закон представляет обратное отношение к тому, которое открывается в предыдущем:
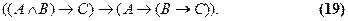
и так же легко обнаруживает свой общезначимый характер:
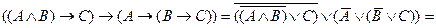
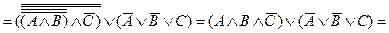
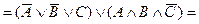
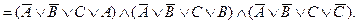
Закон транспозиции. Соотношение логических союзов, названное законом транспозиции, было известно еще древним логикам из философской школы стоиков. Этот закон они даже доказывали. Нормальные формы ими, правда, не использовались. Их доказательства основаны на рассуждениях о логических союзах и их комбинациях. Но так делается и в современных учебниках по символической логике. В древних системах счисления нет также символов. Вместо них используются числительные. Конъюнктивное выражение в их передаче будет звучать: «Есть первое и второе», импликация у них выражается так: «Если есть первое, то есть и второе». Формула этого закона выглядит следующим образом:
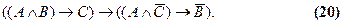
Чтобы придать ему наглядность, возьмем высказывание «Если товар ходовой и рентабельный, то мы получим прибыль». Согласно закону транспозиции при верности такого высказывания должно быть истинным также и высказывание «Если товар ходовой, но прибыли нет, то, значит, товар не рентабельный». Для сведения выражения к нормальной форме избавимся сначала от импликаций, а затем от отрицаний над скобками:
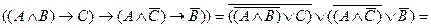
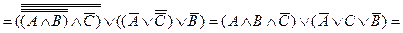
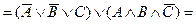
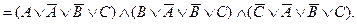
По такой методике можно исследовать и все остальные выражения логики высказываний. Правда, когда заранее неизвестно, к какой категории относится анализируемое выражение, тогда приходится приводить его сначала к КНФ и, если оно не является тождественно-истинным, то тогда надо еще привести его и к ДНФ. Если же оно и к тождественно-ложным не относится, то значит перед нами нейтральное выражение.
Допустим, предстоит провести проверку такой формулы:
(p®q)Ù(p®r)®(p®(qÙr).
Для этого нам надо сначала привести ее к нормальной форме, избавляя от импликаций по формуле (7) и появляющихся вследствие этого отрицаний над скобками по формулам (2) и (4), тогда придем к выражению:
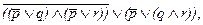
которое далее может быть преобразовано в дизъюнктивную нормальную форму (ДНФ):
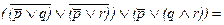
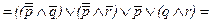
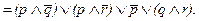
Из нее видно, что нет даже хотя бы только одного дизъюнкта, в котором элементарная конъюнкция включала бы в себя переменную вместе с ее отрицанием. Отсюда - данная формула не относится к разряду тождественно-ложных.
Остается узнать, является ли она тождественно-истинной, для чего надо полученную нормальную форму свести к КНФ. В этом случае сведение будет много сложнее. Сначала сгруппируем выражение в две большие скобки и применим к каждой из них правило дистрибутивности (13):
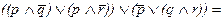
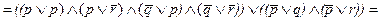
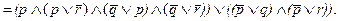
У нас получилось две конъюнктивные нормальные формы – одна в большой скобке справа, другая – слева. Мы можем применить к ним правило дистрибутивности (12), рассматривая каждую маленькую скобку (в одном случае символ p) как одну переменную и учитывая, что самих переменных больше, чем указано в правиле. Тогда каждая такая скобка из левой части будет сочетаться с каждой из правой:
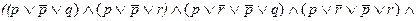
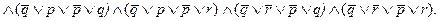
Из полученной конъюнктивной нормальной формы видно, что в каждой из ее элементарных дизъюнкций обязательно находится хотя бы одна переменная вместе с ее отрицанием. Следовательно, все конъюнкты тождественно-истинны, а значит и исходное выражение тоже. Можно поэтому утверждать, что взятая нами для анализа формула представляет собой один из законов логики высказываний.
Из других законов логики высказываний полезно помнить еще закон исключения:
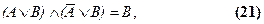
законы поглощения:


и законы выявления:
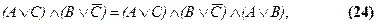
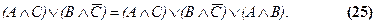
С их помощью можно упрощать сложные выражения, что существенно облегчает проведение преобразований.
Глава II. Логика предикатов
Понятие в логике предикатов. Специфика понятия в логике предикатов лучше всего может быть пояснена через раскрытие его отношения к высказыванию. Для этого надо представить понятие в качестве высказывательной функции или формы высказывания, как это делает немецкий автор В. Зегет, отрывки из книги которого “Элементарная логика” использованы в этом разделе. Высказывательной функцией является, например, “x - студент-заочник” и “x - отец y”. Как известно, каждое высказывание обладает свойством быть либо истинным, либо ложным. Очевидно, что приведенные в качестве примеров выражения с этой точки зрения не могут быть оценены. Поэтому они не являются высказываниями; по этой причине их лучше назвать высказывательными функциями. Они ничего не утверждают и ничего не отрицают, а представляют собой незаконченные, незавершенные высказывания и имеют, по крайней мере, одну переменную величину (x, y), представляющую собой так называемую свободную переменную. В высказывании же, точнее в его языковом выражении, нет никакой свободной переменной. Не давая пока определения свободной переменной, будем на этой стадии рассмотрения считать ее переменной, которая еще не имеет значения.
Существуют два способа перехода от понятия как высказывательной функции к высказыванию. Первый заключается в завершении высказывательной функции до высказывания путем замены свободной переменной подходящими конкретными именами. Так из “x - студент-заочник”, заменяя переменную x именем “Петр Морозов”, получаем повествовательное предложение “Петр Морозов - студент-заочник”. Это выражение обязательно является либо истинным, либо ложным, смотря по тому, учится на заочном отделении или нет подразумеваемый Петр Морозов. Из “x - отец y” повествовательное предложение получается лишь тогда, когда обе свободные переменные заменены собственными именами, например: “Степан Павлович Титов - отец Германа Степановича Титова”.
Приведенные в качестве примеров переменные - это индивидные переменные. Они представляют собой как бы пустые места для собственных имен, т.е. для языковых выражений, которые однозначно именуют конкретные индивиды. В результате применения первого способа к содержащим такие переменные высказывательным функциям получаются единичные высказывания.
Второй путь получения предложения из высказывательной функции заключается в связывании свободных переменных. Это происходит с помощью операторов или кванторов. Из высказывательной функции “x - студент-заочник”, используя квантор существования, получают высказывание о существовании:
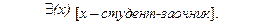
Это значит: “Существует, по крайней мере, один индивид, для которого верно, что x - студент-заочник”. Совершенно очевидно, что квантор превратил выражение в такое, что теперь оно обязательно является либо истинным, либо ложным в зависимости от того, что подразумевается под x. Оно истинно, если x - люди вообще, и оно ложно, если x означает какую-то конкретную группу лиц, среди которых нет ни одного заочника.
Из высказывательной функции “x - отец y” с помощью двух кванторов существования получают высказывание о существовании:
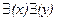 [x – отец y].
[x – отец y].
Это значит: “Существуют, по крайней мере, один x и один y, для которых верно, что x - отец y”. Можно также получить высказывание
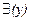 [С.П.Титов – отец y].
[С.П.Титов – отец y].
Одна переменная заменена в нем на индивидуальное имя, другая осталась свободной, вернее, ограниченной только квантором. Теперь это полу символическое выражение означает, что существует некий y, для которого верно, что С.П. Титов - его отец. Важно, чтобы были учтены все свободные переменные. Оба этих выражения тоже сходны с высказыванием в том отношении, что они также могут быть оценены с точки зрения истинности.
Теперь о другом кванторе. Из высказывательной функции “x - студент-заочник” с помощью квантора общности получают высказывание обо всех индивидах:
[x – студент-заочник],
то есть для каждого индивида x верно: “x - студент-заочник”. С помощью квантора общности выражают, что каждому отдельному индивиду определенной области принадлежит данный признак.
Применяя два квантора общности к этой же самой высказывательной функции, можно получить следующее ложное высказывание:
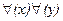 [x - отец y].
[x - отец y].
Это значит: “Для каждого x и для каждого y верно: x - отец y”, иными словами: “Каждый является отцом каждого”. В результате комбинированного применения квантора общности и использования собственных имен также получаются высказывания обо всех индивидах.
Могут быть и высказывания, в которых используются оба типа кванторов, например:
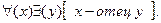
Если индивидная область - область людей, то эта запись выражает высказывание “Каждый человек имеет отца”.
Итак, высказывательные функции превращаются в высказывания путем замены содержащихся в них свободных переменных именами собственными или путем связывания их кванторами. Квантор связывает все находящиеся в области его действия свободные переменные. В область действия квантора всегда входит, по крайней мере, последующая высказывательная функция. В нее может одновременно входить и несколько высказывательных функций, соединенных логическими связками. В этом случае все высказывательные функции, находящиеся в области действия квантора, объединяются скобками.
Два вида переменных, о которых здесь шла речь, можно определить следующим образом:
Переменная является свободной переменной, если она не находится в области действия квантора.
Переменная является связанной переменной, если она находится в области действия квантора.
Может удивить, что в разделе о логике предикатов не было еще и речи о предикатах. Теперь их введение подготовлено, так что уже можно несколькими фразами объяснить, что такое предикаты, какой смысл будет вкладываться в это понятие в данном разделе символической логики.
Предикаты - это высказывательные функции типа “x - студент-заочник”, “x больше, чем y”, “x говорит с y о z” и т.д. Их можно считать аналогами понятий традиционной логики, так как в них отражается содержание понятий в их правильной логической форме. Понимаемые так предикаты являются также базовым структурным элементом для образования высказываний логики предикатов и выражения их на символическом языке, принятом в этом разделе символической логики. С этой точки зрения они сходны с предикатами суждений, так как, подобно им, не являются ни истинными, ни ложными, хотя внешне они больше похожи на высказывания. Все, что до сих пор говорилось о высказывательных функциях, относится также и к предикатам, так как каждый предикат является высказывательной функцией.
В приведенных ранее примерах встречаются предикаты с одной и с двумя переменными. В принципе их может быть и три, и четыре, и больше. В этом смысле принято говорить о многоместных предикатах. По числу мест предикаты делятся на:
(1) одноместные предикаты - это отражения свойств, высказывательные функции с одной переменной,
(2) многоместные предикаты - это отражения отношений, высказывательные функции более чем с одной переменной.
Многоместные предикаты более строго подразделяются на двухместные, трехместные и т.д. предикаты или отношения.
Когда перед нами двухместный предикат, то его содержание может быть выражено как суждение, отмечающее разные отношения, - любить, ненавидеть, быть больше или меньше, находиться дальше или ближе и т.п. Допустим, L у нас означает любить. Тогда, пользуясь языком логики предикатов, можно записать:
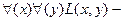 все любят всех;
все любят всех;
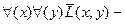 все не любят всех;
все не любят всех;
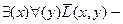 некоторые не любят всех;
некоторые не любят всех;
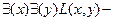 некоторые кого-нибудь любят.
некоторые кого-нибудь любят.
В логике предикатов к каждой такой записи надо обязательно указывать предметную область, к которой относится высказывание. Это называется задать универсум для переменных. Так, x и y могут означать людей. Тогда выражение
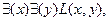
где x, y - люди,
является истинным высказыванием: “Некоторые люди кого-нибудь любят”.
А выражение
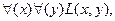
где x - кошки, y - собаки,
означающее, что кошки любят собак, будет ложным высказыванием.
Допустим затем, что нам надо проверить истинность высказывания 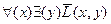 , где L(x, y) также означает, что “x любит y”, а универсумом являются персонажи “Анны Карениной”: Анна, Вронский, Каренин. Сделанная нами символическая запись, очевидно, означает: “Все кого-нибудь не любят”. И чтобы проверить ее значение истинности, надо перебрать все варианты отношений между персонажами:
, где L(x, y) также означает, что “x любит y”, а универсумом являются персонажи “Анны Карениной”: Анна, Вронский, Каренин. Сделанная нами символическая запись, очевидно, означает: “Все кого-нибудь не любят”. И чтобы проверить ее значение истинности, надо перебрать все варианты отношений между персонажами:
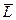 (Анна, Вронский) - ложно.
(Анна, Вронский) - ложно.
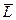 (Анна, Каренин) - истинно.
(Анна, Каренин) - истинно.
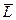 (Вронский, Анна) - ложно.
(Вронский, Анна) - ложно.
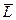 (Вронский, Каренин) - истинно.
(Вронский, Каренин) - истинно.
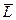 (Каренин, Анна) - ложно.
(Каренин, Анна) - ложно.
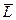 (Каренин, Вронский) - истинно.
(Каренин, Вронский) - истинно.
Из этого перечня видно, что каждый из персонажей в самом деле кого-нибудь не любит, следовательно, на рассматриваемом нами универсуме формула 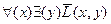 дает истинное высказывание.
дает истинное высказывание.
Трехместные предикаты выражают более сложные взаимоотношения. Например, выражение
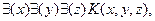
где x, y, z - люди,
может быть интерпретировано так: некий x получает кредит у какого-то y с помощью рекомендации от z.
Суждение в логике предикатов. Теперь можно перейти и к суждениям. В работе с суждениями логика предикатов опирается на исчисление высказываний и представляет собой его дальнейшее продолжение. Но в отличие от того, как делается там, здесь снова принимается во внимание структура суждения - деление на субъект и предикат, хотя записываются они уже иначе, чем в традиционной логике. Можно, разумеется, записывать как общие суждения, так и частные, а также утвердительные и отрицательные.
Общеутвердительное суждение в логике предикатов запишется в следующем виде:
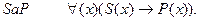
Читается это выражение так: “Для любого x верно, что если оно обладает свойством S, то тогда оно обладает и свойством P”. Если бы, допустим, у нас было общеутвердительное суждение “Всякий товар обменивается на деньги”, то тогда на языке логики предикатов оно звучало бы так: “Для всякой вещи верно, что если она - товар, то тогда она обменивается на деньги”. Такая формулировка кажется неудобной, громоздкой грамматической конструкцией, но для целей символической логики она более удобна.
Общеотрицательное суждение тоже записывается с помощью импликации, только свойство, отмечаемое в обычном суждении в предикате, записывается с отрицанием. Суждение “Ни одна мышь - не хищник” в символическом виде будет выглядеть так:
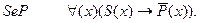
Если x обладает свойством быть мышью, то не обладает свойством быть хищником.
Частные суждения (утвердительные и отрицательные) записываются с помощью квантора существования. А вместо импликации берется конъюнкция. Употребление именно этого квантора должно быть понятно само собой, ведь он предназначен для выражения частных суждений: существует x, обладающий такими-то свойствами, означает то же самое, что некоторые x обладают этими свойствами. Замена же импликации на конъюнкцию объясняется тем, что свойство, отмечаемое в предикате, принадлежит (не принадлежит) только части предметов, о которых говорится в субъекте; это значит, утверждение об обладании этим свойством нельзя считать следствием того, что мы взяли такие предметы, для которых оно непреложно необходимо. Предмет и такое-то свойство просто соседствуют иногда. Поэтому конъюнкция более уместна для выражения их взаимоотношений.
Частноутвердительное суждение, например, такое: “Некоторые книги - учебники” запишется формулой:
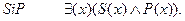
Существует по меньшей мере одно x, для которого верно будет сказать, что оно обладает свойством S (быть книгой) и одновременно свойством P (быть учебником).
Частноотрицательное суждение, например: “Некоторые города - не столицы” получает такое выражение:
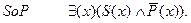
Существует хотя бы одно x, для которого верно, что оно - город и в то же время не столица.
Таким образом, мы перебрали все виды суждений и, следовательно, теперь можем записывать любые их комбинации. Выведем в качестве примера формулу для такого сложного суждения: “Все адвокаты - юристы, а некоторые имеют второе образование”.
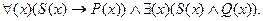
S означает здесь быть адвокатом, P - быть юристом, Q - иметь второе образование. Это выражение можно при желании преобразовывать, как формулу логики высказываний.
Законы логики предикатов. Законами в логике предикатов, как и в логике высказываний, являются общезначимые выражения, то есть такие, которые остаются истинными при любых наборах переменных. Причем выражения общезначимые в логике высказываний остаются таковыми и в логике предикатов. Так, законы эквивалентных преобразований, выражаемые в предыдущем разделе формулами 2-9, как и другие законы, могут быть перенесены и сюда тоже. Достаточно заменить использовавшиеся там переменные A и B на предикаты (в том числе и многоместные) F(x), G(x), F(x,y), G(x,y) и т.д. и тогда получатся выражения логики предикатов. Так формула (3) для преобразования конъюнкции в импликацию получит такое выражение для одно- и двухместных предикатов:
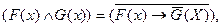
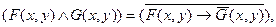
а формула (6) для преобразования импликации в конъюнкцию получит такой вид:
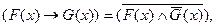
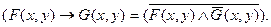
Аналогичным образом можно превратить в законы логики предикатов и остальные общезначимые формулы логики высказываний. Однако в логике предикатов к этим законам добавляются еще и свои законы. Это прежде всего связано с тем, что здесь помимо переменных вводятся еще и кванторы. Так что приведенные выше две пары общезначимых выражений логики предикатов, переделанные из формул предыдущего раздела, еще имеют мало сходства с выражениями собственно логики предикатов, так как не содержат кванторов. Для оперирования ими разработаны специальные правила.
Правила преобразования кванторов. В разговорах и в текстах приходится довольно часто подвергать отрицанию слова “все”, “каждый”, “некоторые”, “отчасти” и т.п. Могут, например, сказать, что не все студенты изучают второй иностранный язык, или: неверно, будто формулы данной логической системы были частично переработаны, они все подверглись переработке. На языке символической логики это называется отрицанием кванторов. Так, запись 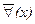 означает: “Не для всех x...” или “Неверно, что для всех x...”. А
означает: “Не для всех x...” или “Неверно, что для всех x...”. А 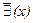 - соответственно: “Не существует x...” или “Неверно, что некоторые x...”
- соответственно: “Не существует x...” или “Неверно, что некоторые x...”
Мы укажем сначала все вообще правила преобразования (замены) кванторов. Правила для отрицания выделим среди них потом. Взаимная замена кванторов производится по следующим формулам:
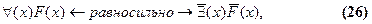
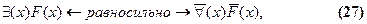
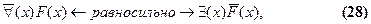
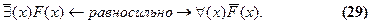
Для многоместных предикатов формулы аналогичны. Записывать их отдельно нет необходимости, так как в них все так же, как и в этих, только предикаты одно-, двух- и многоместные.
Преобразование квантора требует, как видим, чтобы над новым, сменяющим, квантором появилось отрицание и вдобавок надо отрицать подкванторное выражение (предикат). Две последние строчки в перечне формул (28) и (29) представляют собой правила отрицания кванторов. Они производны от формул (26) и (27) и могут быть при желании получены из них. В самом деле, допустим, у нас имеется выражение 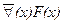 и мы хотим заменить в нем квантор, воспользовавшись формулой (26). Тогда, значит, надо заменить
и мы хотим заменить в нем квантор, воспользовавшись формулой (26). Тогда, значит, надо заменить 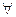 на
на 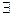 и поставить над последним знак отрицания. А так как в исходном выражении над квантором уже стоит одно отрицание, то, следователдьно, их будет теперь два. Кроме того, надо поставить отрицание над F(x).
и поставить над последним знак отрицания. А так как в исходном выражении над квантором уже стоит одно отрицание, то, следователдьно, их будет теперь два. Кроме того, надо поставить отрицание над F(x).
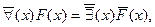
учитывая взаимную нейтрализацию двух отрицаний, получим:
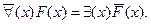
Получилась как раз формула (28). Точно таким же путем можно из (27) получить (29), а сами исходные для последнего рассуждения формулы (26) и (27) доказываются с помощью сложных математических теорем. Поэтому в дальнейшем мы будем считать данные правила
Дата добавления: 2020-06-09; просмотров: 755;











