Основные тенденции в современной логике

Как и всякая другая область знания, логика непрерывно развивается. Наиболее интенсивно она стала прогрессировать с середины девятнадцатого века, когда ряд математиков взялись разрабатывать и внедрять идеи символической логики. Отсюда возникает самая заметная тенденция в современной логике - ее математизация. Поначалу она поддерживалась только тем, что разработки по символической логике предназначались именно для решения некоторых трудных проблем "царицы наук". Поэтому здесь она и поныне называется логикой математической. Такое название лучше всего и дальше сохранить для ее максимально строгого и предельно формализованного изложения. А под символической логикой следует, как представляется, понимать ее популяризированный вариант.

Но в настоящее время стремление вводить в логику математические методы и выражать ее идеи на языке формул и символов объясняется также и целым рядом удобств, которые отсюда проистекают: точность, краткость, емкость изложения, возможность легко получать и обозревать следствия. К тому же математизированная символическая логика расширяет возможности логики традиционной. Скажем, пользуясь языком логики предикатов, можно обосновать некоторые дополнительные виды силлогизмов, что было бы невозможно сделать прежними методами. В последнее время появились попытки даже учебники по традиционной логике изложить на языке формул. У многих авторов и то, и другое изложения перемежаются. Нарастание роли компьютеров, надо думать, еще дальше подхлестнет процесс перевода понятий традиционной логики на предельно математизированные искусственные языки символов.

Наряду с этим для современной логики характерны неуклонно нарастающие специализация и дифференциация. Постоянно возникают новые ответвления и отрасли. Отчасти они продолжают развивать и разрабатывать идеи, зародившиеся еще в традиционной логике, но теперь дополняемые и расширяемые. Таковы, к примеру, модальные логические системы. Еще больше новых разделов вырастает в собственно символической логике. В них создаются логические средства решения каких-либо узко специальных задач или они могут заниматься исследованием отдельных проблем.

Значительная часть разработок такого рода занята уточнением закона исключенного третьего, поскольку его применение к бесконечным множествам, как уже отмечалось ранее, порождает немало трудных вопросов. Создаваемые здесь концепции называют интуиционистскими, или конструктивными.

Еще одно направление в исследованиях ориентировано на разрешение парадоксов импликации. Этим обозначают тот факт, что импликативные высказывания и таблица истинности для них лишь более или менее упрощенно передают содержание действительных связей между условием и обусловленным. Так, два ложных предложения, связанные импликацией, всегда образуют, как мы помним, истинное высказывание, при ложном антецеденте импликация будет всегда истинной, при истинном консеквенте она тоже всегда истинна. Обычно все это записывают с помощью формул.

Мы возьмем для пояснения лишь две из них:

a) (p Ù 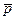) ® q, b) q ® (p Ú ).

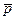Антецедент в первой является противоречием, поэтому всегда ложен. Присоединяйте к нему в качестве консеквента любую мысль q (пусть даже нелепую) и она будет обоснована, так как формула представляет собой закон - выражение истинное при любом значении переменных. Это можно было бы назвать порочным всесилием аппарата, построенного на такой импликации: с его помощью доказывается все, что угодно. Во второй формуле консеквент является всегда истинным выражением и поэтому на месте антецедента может оказаться любое высказывание q. Здесь получается, что истинную мысль можно считать выводимой из всего, что угодно.

Сначала уточнение было сделано с помощью понятия строгой импликации (обычную же импликацию стали в силу этих обстоятельств именовать материальной). Предполагалось считать импликативными в строгом смысле только необходимые взаимоотношения условия и обусловленного. Однако в дальнейшем выяснилось, что такой подход не избавляет от парадоксов. В настоящее время исследование этих вопросов разрослось в довольно широкое течение, в рамках которого создаются разнообразные варианты релевантных систем счисления. С их помощью вводятся различные ограничения и уточнения, призванные свести импликативные взаимоотношения к реальным связям, исключив из них возможные искусственные и чисто формальные импликации. Наиболее удачными из всех имеющихся релевантных логик пока следует, видимо, признать те, которые считают связанными импликацией лишь выражения, имеющие общие элементы. Этим отбрасывается очень много чисто надуманных импликативных образований и теория импликации становится более реальной моделью условных связей. Однако до удовлетворительного решения всех вопросов и проблем в этой области пока еще далеко.

В последние несколько десятилетий заметную область исследования стали составлять проблемы, называемые интенсиональными. Чтобы их понять, надо сначала познакомиться еще с одной разновидностью парадоксов, получивших название антиномий отношения именования. Допустим, перед нами такое истинное высказывание: "Убийцы журналиста Листьева совершили преступление такого-то числа в таком-то месте Москвы". Поскольку в суждении используются два равнозначных понятия, то обычно одно из них может заменять другое. Мы можем, например, сказать, что убийцы журналиста Листьева должны предстать перед судом, а отсюда, произведя замену, получить истинный вывод о том, что лица, совершившие преступление такого-то числа в таком-то месте Москвы, должны предстать перед судом. Следовательно, из двух истинных предложений путем эквивалентной замены мы получим истинное утверждение. Но оказывается, что иногда такая процедура странным образом приводит к ложным выводам из истинных посылок.

Для того чтобы убедиться в этом, достаточно взять такое предложение: "Генеральный прокурор утверждал, что убийцы журналиста Листьева совершили преступление такого-то числа в таком-то месте Москвы". Если здесь заменить понятие "совершившие преступление такого-то числа в таком-то месте Москвы" на "убийцы журналиста Листьева", то получится: "Генеральный прокурор утверждал, что убийцы журналиста Листьева есть убийцы журналиста Листьева". Думается, что такие пустопорожние банальности любой оратор назовет искажением его слов.

Аналогичным путем можно превратить в ложное и такое предложение: "Политик в своем выступлении отметил, что война есть самое страшное бедствие". После проведения замены получится: "Политик в своем выступлении отметил, что война есть война".

Ряд исследователей полагают, что парадоксы заставляют различать контексты на экстенсиональные, где принцип взаимозаменимости действует без ограничений, и интенсиональные, где он перестает быть универсальным. Согласно мнению других, принцип взаимозаменимости не нуждается в ограничениях. Само отношение именования имеет разный характер для эмпирических и абстрактных объектов. При последовательном проведении этого различения, считают они, парадоксов можно будет избежать.

Сама по себе эта проблематика в принципе затрагивалась раньше Гегелем, хотя подходил он к ней с другой стороны. По его представлению, в любом суждении субъект и предикат обязательно отличаются друг от друга и потому полное отождествление одного с другим вообще бессмысленно. Это особенно заметно на примере определений. Если мы хотим объяснить, что такое, допустим, комета, то нам придется обратиться к каким-то отличающимся от этого небесного тела понятиям: имеет замкнутую орбиту, за ней тянется хвост и т. д. Стремление же дать именно тождественную формулировку приведет к бессодержательной тавтологии: комета есть комета. В реальном определении отождествляется различное и потому в нем всегда есть какая-то доля противоречия. Интенсиональные контексты высвечивают один из аспектов этой старой проблемы. Сам Гегель делал отсюда вывод, что такие противоречия надо не устранять, а изучать, чтобы научиться учитывать и использовать их в логических операциях.

В начале учебника уже говорилось о попытках создавать неклассические логики. Это еще одна значительная черта современной логики. В таких системах вместо аристотелевских законов формулируются другие, альтернативные им. Наиболее экстравагантными из таких систем и в то же время наиболее примечательными являются те, в которых отменяется жесткий запрет на противоречие и наряду с непротиворечивыми высказываниями допускаются также противоречащие. Заслуживает особого рассмотрения также логическое конструирование.