Противоречия - это формулы логики высказываний, принимающие значения «ложь» при любом наборе своих пропозициональных переменных.

Не надо, однако, смотреть на формулы-противоречия как на какую-то досадную помеху в логике высказываний. Во-первых, превращение их в законы осуществляется простым отрицанием (это отличает противоречия символической логики от противоречий в логике традиционной). Так, закон противоречия представляет собой простое отрицание тождественно-ложного выражения Во-вторых, постоянство семантического значения, даже ложного, все равно дает основу для анализа высказывания, записанного с помощью тождественно-ложной формулы. В-третьих, они, так же как и тождественно-истинные выражения, помогают осуществлять логические преобразования, упрощать когда надо сложные формулы.

Последняя категория выражений символической логики имеет в наборе своих значений как «истину», так и «ложь». Такой является третья из приведенных нами формул. Выражения данной разновидности называют нейтральными.

Нейтральными являются высказывания, которые хотя бы при одном сочетании значений своих пропозициональных переменных становятся истинными высказываниями и хотя бы при одном - ложными.

Поскольку истинностные значения таких формул остаются неизвестными, то при анализе высказываний их приходится каждый раз вычислять. Но это не дает основания относить нейтральные формулы к так сказать побочным продуктам логических разработок. Правда, в преобразованиях их использование сводится к нулю. Но символическая запись выражений имеет ведь не только это предназначение. Их более важной функцией является превращение словесных высказываний в формулы, которые оставались бы после этого адекватным воспроизведением действительности. Эта функция осуществляется через интерпретацию формул. С точки зрения отображения реальности во всей ее неповторимой конкретности нейтральные выражения имеют даже преимущества перед законами и противоречиями, вернее сказать, они не заменимы ничем иным на своем месте. Ибо законы воспроизводят самые общие черты действительного мира, а единичные явления через них не отображаются. Для этого подходят только нейтральные выражения.

Возьмем для примера такую формулу:

Просчитав по методу нуля и единицы все ее возможные значения, нетрудно убедиться, что она представляет собой закон - тождественно-истинную формулу. В качестве интерпретации можно взять, допустим, родственные взаимоотношения: «Она приходится ему или сестрой (p) , или кузиной (q) и при этом известно, что она - не сестра, следовательно, она ему доводится кузиной». С первого взгляда может показаться, что общезначимость этой формулы говорит о ее хорошем соответствии реальности. Но на самом деле, как можно убедиться, соответствие тут скорее должно быть частичным - лишь при некоторых семантических значениях переменных. В самом деле общезначимость выражения заставляет признать, что и при обоих ложных простых высказываниях оно будет истинным; стало быть, на деле она не будет доводиться ему ни сестрой (p=0), ни кузиной (q=0) а мы, просчитав формулу при этих значениях переменных, сделаем вывод, что она ему все-таки приходится кузиной, и должны считать этот вывод правильным.

Дело здесь не в несовершенстве аппарата символической логики. Просто данная ситуация не должна описываться общезначимой формулой. Более корректной являлась бы такая, которая приводила бы к истинному высказыванию при разных семантических значениях переменных (истинно, что она - сестра, и неистинно, что кузина, или наоборот) и к ложному в случае, когда оба они ложны. К такой формуле можно прийти, если усилить вывод об осуществлении одной из альтернатив при неосуществлении другой записью того, что отсутствие одной из этих альтернатив обязательно ведет к наличию другой, например, в таком виде:

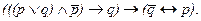
Такое выражение дает ложное высказывание при подстановке в нее на место букв двух ложных простых суждений и в то же время при разных значениях последних, оно, как и первая формула, превращается в истинное утверждение. Причем истинность формул зависит от сочетания значений переменных, но, однако, не зависит от их содержания. И та, и другая формулы будут всегда приводить к одним и тем же семантическим результатам, идет ли речь о преступнике, который мог проникнуть в помещение через окно или крышу, но через окно не проникал, или еще о каких-нибудь аналогичных альтернативах. В этом смысле обе формулы можно было бы считать законами, но тогда мы использовали бы это понятие в общеупотребительном смысле, а не в том специфическом, который принят в символической логике.

Помимо отмеченных трех видов формул других их разновидностей в логике высказываний нет. Нейтральные выражения и законы составляют вместе класс так называемых выполнимых выражений. Объединяющим их признаком является то, что соответствующие им сложные высказывания реализуемы на практике хотя бы при некоторых условиях.