Практическое приложение уравнения гидростатики

Принцип сообщающихся сосудов. Пусть два открытых сообщающихся сосуда заполнены жидкостью плотностью 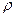(рис. 2.4).

Рассмотрим произвольную плоскость сравнения 0 - 0 и некоторую точку А внутри жидкости, лежащую в этой плоскости. Если считать точку А принадлежащей левому сосуду, то, согласно уравнению (2.2), давление в этой точке равно:

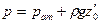Если считать точку А принадлежащей правому сосуду, то давление в ней равно:

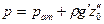
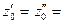( 0, т.к. плоскость 0 - 0 проходит через точку А).

При равновесии для каждой точки давление одинаково в любом направлении, иначе бы происходило перемещение жидкости. Следовательно

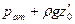
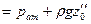
или

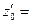
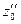Аналогичный вывод можно сделать, если рассмотреть сообщающиеся сосуды, в которых давление над свободной поверхностью жидкости одинаково.

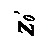
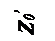
Рис. 2.4. Условия равновесия в сообщающихся сосудах:

а – однородная жидкость; б – разнородные (несмешивающиеся) жидкости

Таким образом, в открытых или закрытых сообщающихся сосудах, находящихся под одинаковым давлением и заполненных однородной жидкостью, уровни последней располагаются на одной высоте независимо от формы и поперечного сечения сосудов.

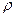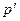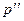Если сосуды заполнены одной жидкостью плотностью , но давления над уровнем жидкости в них неодинаковы и равны и , то

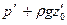
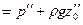
откуда

. (2.3)

Уравнение (2.3) применяется при измерении давлений или разностей давлений с помощью дифференциальных 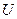-образных манометров.

Пневматическое измерение количества жидкости в подземных резервуарах. Для контроля за количеством жидкости в подземном резервуаре устанавливают трубу, нижний конец которой доходит почти до днища. Давление над жидкостью в резервуаре равно .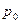

По трубе подают сжатый воздух или другой газ, постепенно повышая его давление, измеряемое манометром. Когда воздух преодолеет сопротивление столба жидкости в резервуаре и начнет барботировать через слой жидкости, давление, измеряемое манометром, перестанет возрастать и станет равным:

.

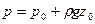Отсюда уровень жидкости в резервуаре равен:

.

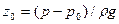По величине и известной площади поперечного сечения резервуара определяют объем находящейся в нем жидкости.

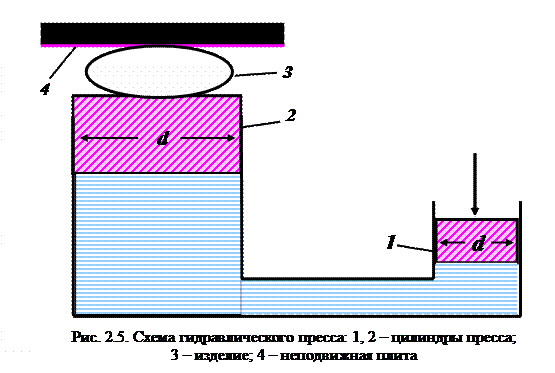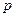Гидростатические машины. На использовании основного уравнения гидростатики основана работа гидравлических прессов, домкратов, гидроцилиндров и др. Если в гидропрессе (рис. 2.5) приложить небольшое усилие к поршню 1, перемещаемому в цилиндре меньшего диаметра , и создать давление на поршень, то, согласно закону Паскаля, такое же давление 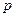будет приходиться на поршень 2 в цилиндре с большим диаметром 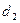, при этом сила давления на поршень 1 составит

,

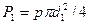а сила давления на поршень 2

.

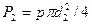В результате поршень в цилиндре большего диаметра передает силу давления во столько раз большую, чем сила, приложенная к поршню в цилиндре меньшего диаметра, насколько поперечное сечение цилиндра 2 больше, чем цилиндра 1.

Давление жидкости на дно и стенки сосуда. Если жидкость помещена в сосуд любой формы, то гидростатическое давление во всех точках горизонтального дна сосуда одинаково, а давление на боковые стенки возрастает с увеличением глубины погружения.

Гидростатическое давление на дно сосуда в соответствии с уравнением гидростатики

,

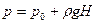где 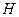– высота жидкости в сосуде.

Сила давления на горизонтальное дно не зависит от формы сосуда и объема жидкости в нем и определяется лишь только высотой столба жидкости и площадью дна сосуда:

.

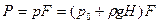Гидростатическое давление жидкости на вертикальную стенку изменяется по высоте. Сила давления на стенку рассчитывается по формуле

,

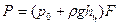где 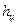– расстояние от верхнего уровня жидкости до центра тяжести смоченной площади F стенки.

Гидродинамика

Движущей силой при течении жидкости является разность давлений, которая создается с помощью насосов или компрессоров, либо вследствие разности уровней или плотностей жидкости.

Знание законов гидродинамики позволяет находить Δp, необходимое для перемещения заданного количества жидкости с требуемой скоростью, а значит и расход энергии на это перемещение. И наоборот, определить скорость и расход жидкости при заданном Δp.

Различают внутреннюю, внешнюю и смешанную задачи гидродинамики.

К внутренней задаче гидродинамики относятся вопросы изучения закономерностей движения жидкости и газов внутри труб и каналов. Внешняя задача связана с изучением закономерностей обтекания жидкостями и газами различных тел (процессы осаждения, механического перемешивания и т.д.). Смешанная задача заключается в изучении движения жидкости и газов через зернистые и пористые слои твердых материалов. Жидкость в этом случае движется одновременно внутри каналов сложной формы и обтекает твердые частицы (процессы фильтрования, течения жидкостей и газов через насадки массообменных аппаратов, реакторов с твердым катализатором и т.п.).