Дифференциальные уравнения движения Эйлера

Рассмотрим установившийся поток идеальной жидкости, движущийся без трения. Как и при выводе дифференциальных уравнений равновесия Эйлера, в потоке движущейся жидкости выделяется элементарный параллелепипед и рассматривается равновесие проекций сил на оси координат. Согласно основному правилу динамики, сумма проекций, действующих на элементарный объем, равна произведению массы жидкости на ее ускорение:

для оси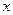

,

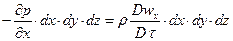для оси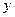

,

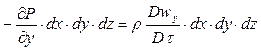для оси z

.

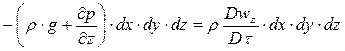Расписав субстанциональные производные проекций скоростей потока по осям пространственных координат:

;

;

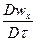
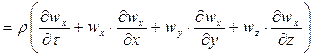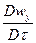
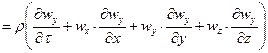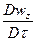
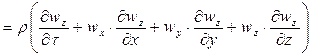
и произведя сокращения, получим для соответствующих проекций дифференциальные уравнения жидкости для неустановившегося потока:

;

;

.

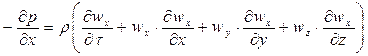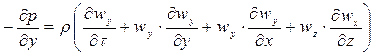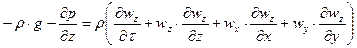Для установившегося потока: 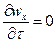, , 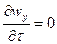, 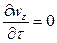тогда:

;

;

.

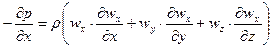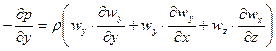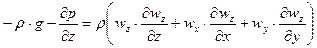Системы уравнений представляют собой дифференциальные уравнения движения идеальной жидкости Эйлера для неустановившегося и установившегося потоков.

Как будет показано ниже, интегралом уравнений движения Эйлера для установившегося потока является уравнение Бернулли, нашедшее широкое распространение для решения многих технических задач.