Основные характеристики движения жидкостей
Гидравлический радиус и эквивалентный диаметр. При движении жидкости через площадь поперечного сечения любой формы, отличающейся от круглой, в качестве расчетного линейного размера применяют гидравлический радиус или эквивалентный диаметр.
Гидравлический радиус 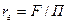 представляет собой отношение площади поперечного сечения трубы или канала, через которое протекает жидкость, к смоченному периметру.
представляет собой отношение площади поперечного сечения трубы или канала, через которое протекает жидкость, к смоченному периметру.
Для круглой трубы:
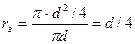 .
.
Диаметр, выраженный через гидравлический радиус, представляет собой эквивалентный диаметр
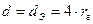 ,
,
следовательно
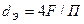 .
.
Эквивалентный диаметр равен диаметру гипотетического трубопровода круглого сечения, для которого отношение площади F к смоченному периметру П то же, что и для заданного трубопровода некруглого сечения.
Для квадрата со сторонами a и b эквивалентный диаметр равен:
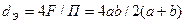 .
.
Для кольцевого сечения с внутренним диаметром D большого трубопровода и наружным малого d:
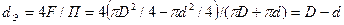 .
.
Для круглой трубы:
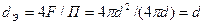 .
.
Установившиеся и неустановившиеся потоки. Движение жидкости называется установившимся или стационарным, если скорости частиц потока и другие параметры, влияющие на его движение, например, 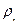 , р, Т, не изменяютсяво времени в каждой фиксированной точке пространства. Расходы жидкости при установившемся течении через поперечные сечения канала также не зависят от времени.
, р, Т, не изменяютсяво времени в каждой фиксированной точке пространства. Расходы жидкости при установившемся течении через поперечные сечения канала также не зависят от времени.
При установившемся движении жидкости проекция скорости 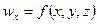 , может быть переменной в любой из точек
, может быть переменной в любой из точек 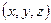 , но не меняется со временем, т.е.
, но не меняется со временем, т.е. 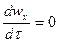 .
.
В отличие от стационарного при неустановившемся или нестационарном потоке факторы, влияющие на движение жидкости, изменяются во времени
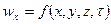 , т.е.
, т.е. 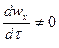 .
.
Установившиеся условия движения жидкости характерны для непрерывных процессов химической технологии. Неустановившееся течение жидкости происходит главным образом в периодических процессах или возникает кратковременно в непрерывных процессах в период пуска или изменения режима работы установки.
Для каждой движущейся частицы жидкости изменение ее параметров во времени и пространстве выражается не частной, а полной производной во времени, называемой в гидродинамике субстанциональнойпроизводной. По смыслу ее называют производной, следующей за потоком.
Обозначим через 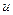 любую величину, изменяющуюся в потоке жидкости как во времени, так и в пространстве, например: плотность, давление, температуру, концентрацию или любую из составляющих скорости
любую величину, изменяющуюся в потоке жидкости как во времени, так и в пространстве, например: плотность, давление, температуру, концентрацию или любую из составляющих скорости 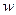 жидкости в направлении осей координат
жидкости в направлении осей координат 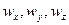 .
.
Допустим, что при наблюдении за движением потока можно мгновенно регистрировать значение параметра 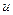 в каждый момент времени и в любой точке потока. Изменение параметра
в каждый момент времени и в любой точке потока. Изменение параметра 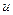 в единицу времени для фиксированной точки пространства
в единицу времени для фиксированной точки пространства 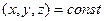 выражается частной производной
выражается частной производной 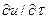 , а изменение
, а изменение 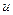 в указанной точке за бесконечно малый промежуток времени
в указанной точке за бесконечно малый промежуток времени 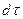 составляет
составляет 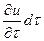 . Это изменение является местнымили локальным изменением данной переменной. При установившемся движении
. Это изменение является местнымили локальным изменением данной переменной. При установившемся движении 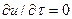 .
.
Если наблюдатель перемещается вместе с потоком, с какой–либо частицей, то за время 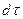 частица потока переместится из точки А с координатами
частица потока переместится из точки А с координатами 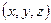 в точку В с координатами
в точку В с координатами 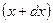 ,
, 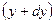 и
и 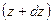 .
.
В результате перемещения из точки А в точку В изменения 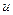 , соответствующие проекциям пути
, соответствующие проекциям пути 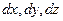 , равны
, равны 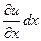 ,
, 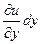 и
и 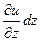 . Эти изменения не связаны с изменением
. Эти изменения не связаны с изменением 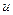 во времени в какой–либо фиксированной точке пространства. Если бы не было локального изменения
во времени в какой–либо фиксированной точке пространства. Если бы не было локального изменения 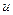 , то при переходе частицы из точки А в точку В значение
, то при переходе частицы из точки А в точку В значение 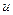 изменилось бы на величину
изменилось бы на величину 
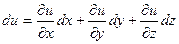 .
.
Это выражение представляет собой конвективное изменение параметра 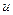 .
.
Полное изменение 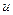 при неустановившемся движении представляет собой сумму локального и конвективного изменений:
при неустановившемся движении представляет собой сумму локального и конвективного изменений:
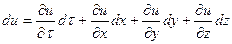 ,
,
откуда изменение параметра за малый промежуток времени:
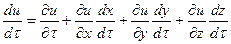 ,
,
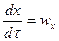 ,
, 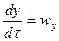 ,
, 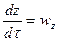 ,
,
тогда
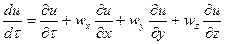 .
.
При установившемся движении 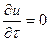 ,
,
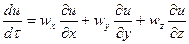 .
.
Последние выражения представляют собой субстанциональную производную для неустановившегося и установившегося течения жидкости. Они характеризуют изменение какого–либо параметра или свойства материи (субстанции) во времени при перемещении материальных частиц в пространстве. С учетом специфики понятия субстанциональную производную зачастую обозначают 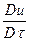 вместо
вместо 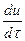 .
.
Уравнение неразрывности (сплошности) потока. Представляет собой зависимость между скоростями в потоке жидкости, для которого соблюдается условие сплошности, или неразрывности течения, т.е. не образуется пустот, не заполненных жидкостью.
Уравнение выражает фундаментальный закон сохранения массы (расхода).
Дифференциальное уравнение неразрывности для неустановившегося течения имеет вид
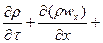
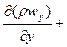
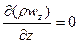 .
.
В установившемся потоке плотность не меняется во времени 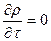 , поэтому уравнение неразрывности выглядит так:
, поэтому уравнение неразрывности выглядит так:
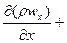
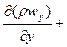
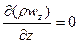 .
.
Для капельных жидкостей, которые практически несжимаемы, а также для газов в условиях изотермического потока, при скоростях меньших скорости звука, 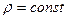 , следовательно, уравнение неразрывности примет вид
, следовательно, уравнение неразрывности примет вид
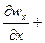
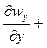
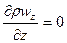 .
.
Для трубопровода постоянного сечения в результате интегрирования дифференциального уравнения неразрывности для установившегося однонаправленного движения жидкости (в направлении оси 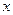 ) получается зависимость
) получается зависимость
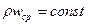 .
.
Если же площадь сечения трубопровода переменна, то интегрирование по площади приводит к зависимости
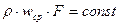 . (2.4)
. (2.4)
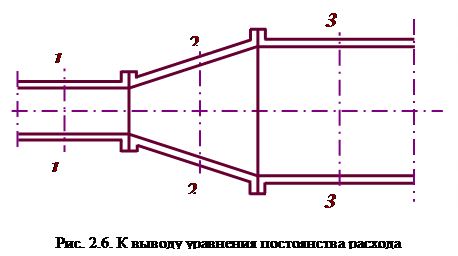
Для трех сечений трубопровода одного и того же потока жидкости (рис.2.6).
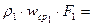
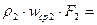
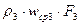
или для массового расхода жидкости в трубопроводе переменного сечения
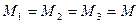 .
.
Согласно уравнению постоянства расхода, при установившемся течении жидкости, полностью заполняющей трубопровод, через каждое его поперечное сечение проходит в единицу времени одно и то же количество жидкости.
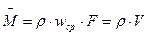 ,
,
при 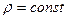
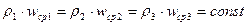 (2.5)
(2.5)
или для объемного расхода жидкости в трубопроводе переменного сечения
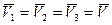 .
.
Из уравнения (2.5) следует, что скорости капельной жидкости в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений.
В соответствии с уравнением (2.4), массовый расход жидкости через начальное сечение трубопровода равен ее расходу через конечное сечение трубопровода. Таким образом, уравнение неразрывности является частным случаем закона сохранения массы и выражает материальный баланс потока.
 |
Скорость и расход жидкости. Количество жидкости, протекающей через поперечное сечение потока в единицу времени, называется расходом жидкости.
Различают объемный (м3/с) и массовый (кг/с) расходы.
В разных точках поперечного сечения потока скорости частиц жидкости неодинаковы, поэтому в расчетах используют не истинные (локальные) скорости, а фиктивную среднюю скорость:
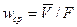 .
.
Объемный расход жидкости равен:
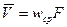 ,
,
массовый расход – 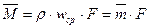 ,
,
массовая скорость жидкости – 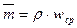 .
.
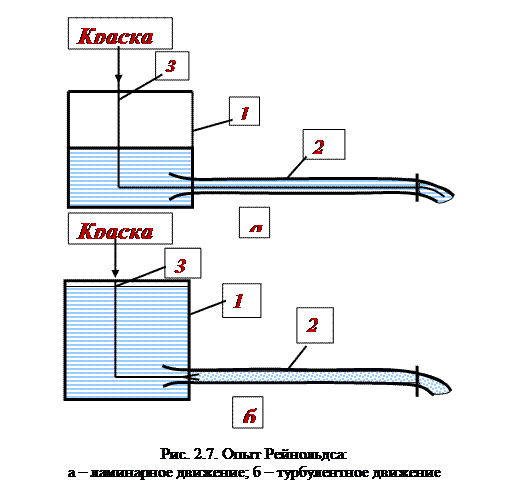
Режимы движения жидкостей. Характер движения жидкости зависит от скорости ее течения. Этот вопрос был решен в 1883 г. О. Рейнольдсом, который поставил простой убедительный опыт. Установка О. Рейнольдса показана на рис. 2.7. Характер движения жидкости устанавливается по степени размытости струйки подкрашенной жидкости, истекающей по трубке 2 из сосуда 1. В зависимости от высоты уровня жидкости в сосуде 1, устанавливалась та или иная скорость течения.
При малых скоростях течения струя окрашенной жидкости 3 не размывалась, что указывало на послойный характер движения жидкости. Такие течения были названы ламинарными.
При некоторой критической скорости струйка размывалась по всему сечению, что свидетельствовало о вихревом характере перемешивания жидкости по всему сечению трубы 4. Такой режим течения был назван турбулентным. Рейнольдс показал, что переход от одного режима течения к другому соответствует определенному значению безразмерной величины:
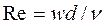
где 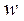 – средняя скорость;
– средняя скорость; 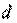 – диаметр канала;
– диаметр канала; 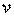 – кинематический коэффициент вязкости жидкости.
– кинематический коэффициент вязкости жидкости.
Безразмерная переменная 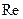 впоследствии был названа числом или критерием Рейнольдса. Переход от ламинарного течения наступает при
впоследствии был названа числом или критерием Рейнольдса. Переход от ламинарного течения наступает при 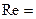 2300. При
2300. При 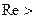 2300 чаще всего наблюдается турбулентный режим течения. Однако при 2300
2300 чаще всего наблюдается турбулентный режим течения. Однако при 2300 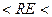 10000 режим течения неустойчиво турбулентный, или переходный.
10000 режим течения неустойчиво турбулентный, или переходный.
Вышесказанное справедливо к стабилизированным изотермическим потокам в прямых трубах с малой шероховатостью стенок. Наличие различных возмущений, обусловленных шероховатостью стенок трубы, изменением скорости или направления течения потока, близость входа в трубу и т. п. могут существенно снизить значения критических чисел Рейнольдса.
Распределение скоростей в движущемся потоке жидкости. Распределение скоростей определяется режимом течения жидкости. При ламинарном режиме распределение может быть установлено законом Стокса:
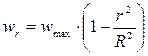 ,
,
представляющим параболическое распределение скоростей в сечении трубопровода, где 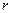 – текущий радиус, отсчитываемый от оси трубопровода;
– текущий радиус, отсчитываемый от оси трубопровода; 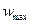 – скорость на оси трубопровода.
– скорость на оси трубопровода.
Средняя скорость по сечению трубопровода связана с максимальной скоростью следующим соотношением:
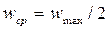 .
.
Уравнение, определяющее объемный расход жидкости при ее ламинарном движении в круглой прямой трубе, носит название уравнения Пуазейля:
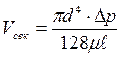 .
.
 |
Турбулентный режим
Турбулентный режимимеет наибольшее распространение в промышленной практике, характеризуется пульсационным движением частиц в продольном и поперечном направлениях по отношению к основному движению потока.
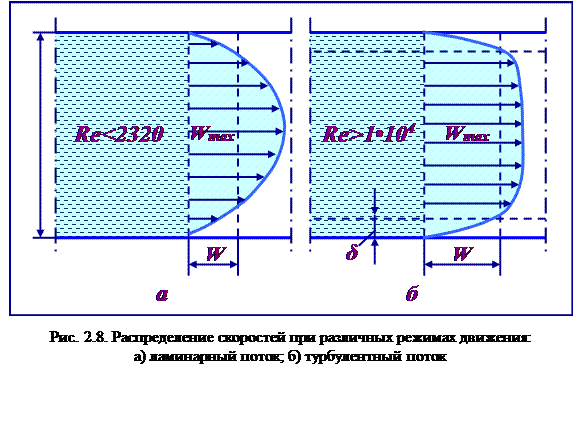
При турбулентном течении из-за хаотического движения частиц происходит выравнивание скоростей в основной массе потока и их распределение по сечению трубы характеризуется кривой, отличающейся по форме от параболы. При этом кривая имеет более широкую вершину (рис. 2.8).
В результате экспериментов установлено, что средняя скорость при турбулентном режиме не равна половине максимальной, как для ламинарного течения, а значительно больше этой величины, причем отношение 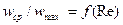 . Например, при
. Например, при 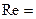 104 скорость
104 скорость 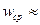 0,8
0,8 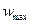 , а при
, а при 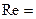 108
108 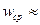 0,9
0,9 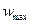 .
.
  |
В связи со сложным характером турбулентного движения не представляется возможным теоретически получить профиль распределения скоростей и значение 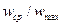 . Кроме того, при турбулентном течении профиль скоростей выражает распределение не истинных, а осредненных во времени скоростей.
. Кроме того, при турбулентном течении профиль скоростей выражает распределение не истинных, а осредненных во времени скоростей.
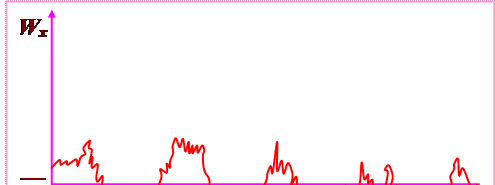
В каждой точке турбулентного потока истинная скорость не остается постоянной во времени из-за хаотического движения частиц. Мгновенные значения скорости испытывают флуктуации, или нерегулярные пульсации, имеющие неустановившийся характер (рис. 2.9).
Истинную скорость измерить практически невозможно из-за хаотического перемещения частиц во всех направлениях. Скорости пульсируют около некоторой усредненной величины, превышая или становясь меньше ее.
Для данной точки величина осредненной во времени скорости может быть найдена из соотношения
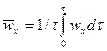 .
.
Разность между истинной и пульсационной скоростями называют мгновенной пульсационной скоростью:
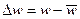 .
.
Причем величина 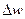 имеет переменный знак. Понятие усредненной скорости не следует путать со средней скоростью потока.
имеет переменный знак. Понятие усредненной скорости не следует путать со средней скоростью потока.
Несмотря на кажущуюся беспорядочность изменения скоростей при турбулентном течении, величина усредненной скорости за достаточно большой промежуток времени 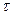 остается постоянной. При этом уже достаточно большим может считаться период времени, измеряемый долями секунды, т. к. частота пульсаций скорости очень высока. Поэтому вместо изменения мгновенных скоростей можно рассматривать независимое от времени изменение усредненных скоростей по сечению трубопровода. В этой связи усреднение скоростей по времени позволяет считать неустановившееся турбулентное течение квазистационарным.
остается постоянной. При этом уже достаточно большим может считаться период времени, измеряемый долями секунды, т. к. частота пульсаций скорости очень высока. Поэтому вместо изменения мгновенных скоростей можно рассматривать независимое от времени изменение усредненных скоростей по сечению трубопровода. В этой связи усреднение скоростей по времени позволяет считать неустановившееся турбулентное течение квазистационарным.
 |
Интенсивность турбулентности выражается отношением
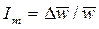 .
.
Средняя квадратичная величина пульсационной скорости, усредненная по всем направлениям, определяется, как
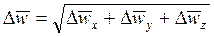 .
.
Интенсивность турбулентности является мерой пульсации в данной точке потока. При турбулентном течении в трубах 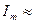 0,01–0,1. Если величины средних пульсаций скорости одинаковы по всем направлениям, то такая турбулентность называется изотропной.
0,01–0,1. Если величины средних пульсаций скорости одинаковы по всем направлениям, то такая турбулентность называется изотропной.
Турбулентность всегда в той или иной степени отличается от изотропной, приближаясь к ней вблизи оси развитого турбулентного потока и все больше отклоняясь от нее в поперечном направлении, по мере приближения к стенке трубы.
К важным характеристикам турбулентного потока относится масштаб турбулентности и турбулентная вязкость. Чем ближе друг к другу находятся две частицы в турбулентном потоке, тем более близки их истинные скорости. В то же время у достаточно удаленных одна от другой частиц нет связи между пульсациями их скоростей. Достаточно близко расположенные частицы, движущие совместно, можно считать принадлежащими к некоторой единой совокупности, называемой обычно вихрем. Размер таких вихрей, или глубина их проникновения, которая может быть отождествлена с расстоянием между двумя ближайшими частицами, уже не принадлежащими к одному вихрю, зависит от степени турбулентности в потоке, или ее масштаба, и поэтому называется масштабом турбулентности.
Для двух частиц, движущихся в направлении оси 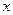 с различными усредненными скоростями и находящихся на расстоянии друг от друга в направлении перпендикулярном оси трубы, выполняется закон Ньютона:
с различными усредненными скоростями и находящихся на расстоянии друг от друга в направлении перпендикулярном оси трубы, выполняется закон Ньютона:
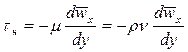 .
.
В ламинарном потоке 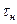 было бы единственным напряжением, возникающим между расположенными на расстоянии
было бы единственным напряжением, возникающим между расположенными на расстоянии 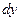 слоями жидкости. Однако в турбулентном потоке частицы перемещаются относительно друг друга не только в продольном, но и в поперечном направлении. Это создает дополнительное касательное напряжение
слоями жидкости. Однако в турбулентном потоке частицы перемещаются относительно друг друга не только в продольном, но и в поперечном направлении. Это создает дополнительное касательное напряжение 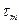 - турбулентное, которое, по аналогии с законом Ньютона, можно выразить уравнением
- турбулентное, которое, по аналогии с законом Ньютона, можно выразить уравнением
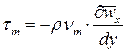 .
.
Величина 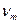 представляет собой кинематический коэффициент турбулентной вязкости. В отличие от обычного коэффициента кинематического коэффициента вязкости
представляет собой кинематический коэффициент турбулентной вязкости. В отличие от обычного коэффициента кинематического коэффициента вязкости 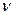 , коэффициент турбулентной вязкости
, коэффициент турбулентной вязкости 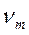 не является физической константой, определяемой природой жидкости, ее температурой и давлением. Турбулентная вязкость зависит от скорости и параметров, определяющих степень турбулентности потока (в частности, расстоянием от стенки трубы и т.д.).
не является физической константой, определяемой природой жидкости, ее температурой и давлением. Турбулентная вязкость зависит от скорости и параметров, определяющих степень турбулентности потока (в частности, расстоянием от стенки трубы и т.д.).
Суммарное касательное напряжение в потоке определяется, следовательно, как вязкостью, так и турбулентностью потока:
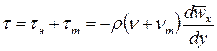 .
.
В основной массе потока скорости жидкости в значительной мере выровнены по сечению трубы. Однако вблизи стенки трубы скорость резко снижается, становясь равной нулю на стенке. Движение жидкости становится менее турбулентным и все более ламинарным, вследствие того, что твердая стенка как бы «гасит» турбулентные пульсации в поперечном направлении. Таким образом, турбулентное течение всегда сопровождается ламинарным.
Условно различают центральную зону, или основную массу жидкости, называемую ядром потока, в которой движение является развитым турбулентным, и гидродинамический пограничный слой вблизи стенки, где происходит переход турбулентного течения в ламинарное.
Внутри этого слоя у стенки имеется тонкий подслой толщиной 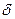 , где силы вязкости оказывают превалирующее влияние на движение жидкости, поэтому характер ее течения в подслое в основном ламинарный. Градиент скорости в ламинарном пограничном подслое очень высок, причем на стенке скорость потока равна нулю.
, где силы вязкости оказывают превалирующее влияние на движение жидкости, поэтому характер ее течения в подслое в основном ламинарный. Градиент скорости в ламинарном пограничном подслое очень высок, причем на стенке скорость потока равна нулю.
Ламинарный подслой в турбулентном потоке характеризуется очень малой толщиной, которая уменьшается с возрастанием турбулентности потока.
Между ядром потока и ламинарным подслоем существует переходная зона, причем ламинарный подслой и эту зону называют гидродинамическим пограничным слоем. Толщина его определяется тем, что напряжения сдвига между частицами жидкости в пограничном слое, обусловленные ее вязкостью и турбулентными пульсациями, а следовательно, значениями 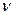 и
и 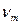 , становятся сравнимыми по порядку величинами.
, становятся сравнимыми по порядку величинами.
Таким образом, структура турбулентного потока состоит из двух зон, четких границ между которыми не существует. Поэтому более правильно использовать представление не о чисто ламинарном, а о вязком подслое, в котором влияние вязкости преобладает над влиянием турбулентных пульсаций, т.е. его толщина характеризуется тем, что в этом подслое 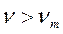 .
.
Дата добавления: 2016-06-29; просмотров: 5317;











