Дифференциальное уравнение теплопроводности

Выделим в однородном теле элементарный параллелепипед объемом dV с ребрами dx, dy, dz. Физические свойства тела – плотность ρ, теплоемкость с, теплопроводность λ – одинаковы во всех точках параллелепипеда и не изменяются во времени. Температура на левой грани dy dx равна t, на противоположной грани .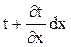

Количество тепла входящего в параллелепипед через его грани за время dτ:

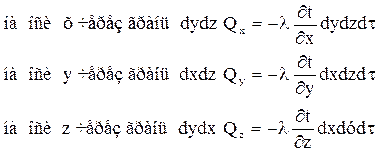
Количество тепла, выходящее из параллелепипеда через противоположные грани за тот же промежуток времени:

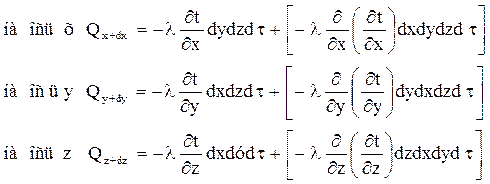
Количество тепла, которое вышло через грань, не равно количеству тепла которое вышло через противоположную грань, т.к. часть тепла расходуется на повышение температуры в объеме параллелепипеда. Разность между количествами вошедшего и вышедшего тепла составит за промежуток dτ:

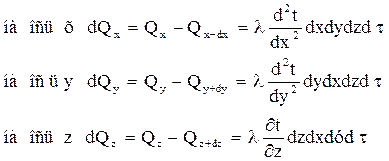
Полное приращение тепла в параллелепипеде за время равно dτ:

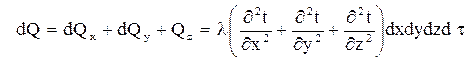
Учитывая что dxdydz = dV получи:

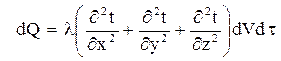
Выражение, стоящее в скобках представляет собой оператор Лапласа 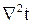. Следовательно:

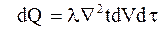(А)

По закону сохранения энергии приращение количества тепла в параллелепипеде равно количеству тепла, расходуемому на изменение энтальпии параллелепипеда, которое составляет:

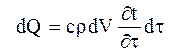(Б)

причем 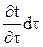представляет собой изменение температуры параллелепипеда за промежуток времени dτ. Приравняем выражение (А) и (Б):

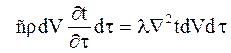
Обозначив 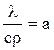и произведя сокращения, получим:

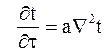(С)

Выражение (С) определяет распределение температур в любой точке тела, через которое тепло передается теплопроводностью, и называется дифференциальным уравнением теплопроводности в неподвижной среде, или уравнение Фурье.

Коэффициент пропорциональности а называется коэффициентом температуропроводности:

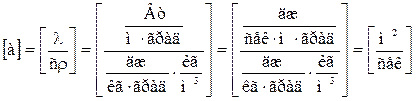
Коэффициент температуропроводности а характеризует теплоинерционные свойства тела: при прочих равных условиях быстрее нагревается или охлаждается тело, которое обладает большим коэффициентом температуропроводности.

При установившемся процесс передачи тепла теплопроводностью 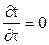и уравнение примет вид: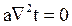

Однако величина а ≠ 0 тогда 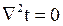, или

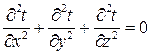
Дифференциальное уравнение теплопроводности в неподвижной среде при установившемся тепловом режиме.

Итоговые уравнения показывают распределение температур при передачи тепла теплопроводностью в общем виде, без учета, в частности, формы тепла, через которое проводится тепло. Для конкретных условий это уравнение должно заполняться граничными условиями, характеризующими геометрические факторы.