Температурное поле и температурный градиент
К числу основных задач теории теплообмена относится установление зависимости между тепловым потоком и распределением температур в средах. Как известно, совокупность мгновенных значений любой величины во всех точках данной среды называется полем этой величины. Соответственно совокупность значений температур в данной момент времени для всех точек рассматриваемой среды называется температурным полем.
При неустановившемся температурном поле температура в данной точке зависит от координат точки (x, y, z) и изменяется во времени, т.е. t = f (x, y, z, τ).
При установившемся поле t = f (x, y, z). Если рассечь тело и соединить точки, лежащие в этой плоскости и имеющие одинаковые температуры, то получим линию постоянных температур – изотерму. В пространстве геометрическое место точек с постоянной температурой представляет собой изотермическую поверхность. Такие поверхности никогда не пересекаются. Пусть разность температур между двумя ближайшими изотермическими поверхностями составляет Δt. Кратчайшими расстоянием между двумя этими поверхностями является расстояние по нормали Δn. При сближении указанных поверхностей отношение Δt/ Δn стремиться в пределу.

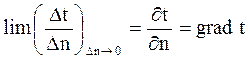
Производная температуры по нормам к изотермической поверхности называется температурным градиентом. Этот градиент является вектором, направление которого соответствует повышению температуры. Величина температурного градиента характеризует наибольшую скорость изменение температуры в данной точке температурного поля.
Поток тепла может возникнуть при условии, что температурный градиент не равен нулю grad t ≠ 0. Перемещение тепла всегда происходит по линии температурного градиента, но направлено в сторону, противоположную этому градиенту.
Дата добавления: 2016-06-29; просмотров: 2202;











