Передача тепла конвекцией (конвективный теплообмен)

Перенос тепла конвекцией тем интенсивней, чем более турбулентно движение массы жидкости. В ядре потока перенос тепла осуществляется одновременно теплопроводностью и конвекцией, причем совместный перенос тепла этими средствами называется конвективным теплообменом. Вблизи стенки образуется тепловой пограничный слой, здесь тепло передается только теплопроводностью. В самом ядер благодаря турбулентным пульсациям температура массы жидкости становится равна t_ж.

Подобно тому, как возрастание вязкости приводит к увеличению гидродинамического пограничного подслоя, возрастание теплопроводности приводит к увеличению теплового пограничного подслоя.

Плотность турбулентного теплообмена:

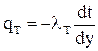
где λ_Т – коэффициент турбулентной теплопроводности.

Величина λ_Т во много раз больше чем λ_..

Интенсивность переноса тепла в ядер потока за счет коэффициента турбулентной теплопроводности определяется коэффициентом турбулентной температуропроводности:

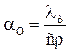
Величина α_Т уменьшается вблизи стенки.

Закон теплоотдачи или закон охлаждения Ньютона:

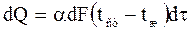
Согласно этому закону, количество тепла dQ, отдаваемое за время dτ поверхностью стенки dF, имеющей температуру t_ж, жидкости с температурой t_ж, прямо пропорционально dF и разности температур t_ст – t_ж

α – коэффициент теплоотдачи характеризует интенсивность переноса тепла между поверхностью тела (стенкой) и окружающей средой (жидкостью).

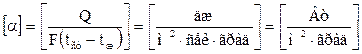
α – показывает, какое количество тепла передается от 1м² поверхности стенки к жидкости (или от жидкости к 1м² поверхности стенки) в течении 1сек при разности температур между стенкой и жидкостью в 1град.

Коэффициент теплоотдачи зависит от следующих факторов:

– скорости жидкости ω, ее плотности ρ и вязкости μ, т.е. от переменных, определяющих режим течения;

– тепловых свойств жидкости, а также коэффициента объемного расширения β;

– геометрических параметров – формы и определяющих размеров стенки, а также шероховатости ε стенки.

Дифференциальное уравнение конвективного теплообмена – или уравнение Фурье – Кирхгофа. Это уравнение выражает в наиболее общем виде распределение температур в движущейся жидкости:

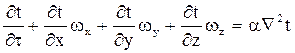
Теплопередача

Плоская стенка. Определяющим количество тепла, которое передается в единицу времени от более нагретой среды с температурой t₁ к менее нагретой с температурой t₂ через разделяющую их стенку.

Стенка состоит из двух слоев с различной теплопроводностью толщина стенки δ₁, с коэффициентом теплопроводности λ₁ и слоя тепловой изоляции толщиной δ₂, с коэффициентом теплопроводности λ₂. Рабочая поверхность стенки F.

Процесс теплообмена установившийся. Следовательно, от более нагретой среды к стенке, сквозь стенку и от стенки к менее нагретой среде за одинаковое время передается одно и то же количество тепла.

Количество тепла, передаваемого за время τ от более нагретой среды, к стенке, по уравнению теплоотдачи составляет:

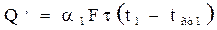
Количество тепла, проходящего путем теплопроводности через слои стенки:

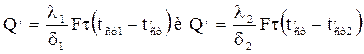
Количество тепла, отдаваемое стенкой менее нагретой среде:

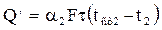
Полученные выражения для Q^, могут быть представлены в следующем виде:

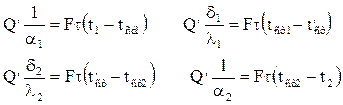
Сложив эти уравнения, получим:

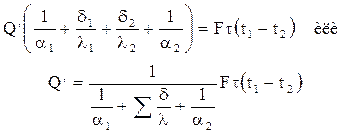
Соответственно при τ = 1

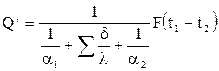
К – коэффициент теплопередачи: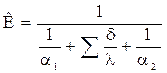

Соответственно уравнение теплопередачи для плоской стенки при постоянных температурах теплоносителей имеет вид:

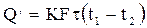
для непрерывных процессов:

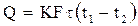
Коэффициент теплопередачи К показывает, какое количество тепла переходит в единицу времени от более нагретого к менее нагретому теплоносителю через разделяющую их стенку поверхностью 1м² при разности температур между теплоносителей на 1град.

Величина, обратная К, называется общим термически сопротивлением:

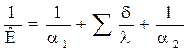
где 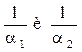– термическое сопротивление более нагретой и мене нагретой среды;

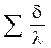– термическое сопротивление многослойной стенки.

Цилиндрическая стенка. Допустим, внутри трубы находится более нагретый теплоноситель с температурой t₁ и коэффициент теплоотдачи от него к внутренней поверхности цилиндрической стенки α_В. Снаружи трубы – более холодный теплоноситель, имеющий температуру t₂. Коэффициент теплоотдачи от наружной поверхности стенки к более холодному теплоносителю α_Н

Проводя аналогичные расчеты, получим:

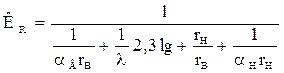
где К_R – линейный коэффициент теплопередачи, отнесенный к единице длины трубы, а не к единице поверхности.

На практике это уравнение применяется только для толстостенных цилиндрических стенок, трубопроводов покрытых толстым слоем тепловой изоляции.

Процессы теплопередачи при постоянных температурах распространены редко (с одной стороны кипит жидкость, с другой стороны стенки конденсируется пар). Наиболее часто теплопередача в промышленной аппаратуре протекает при переменных температурах теплоносителей.

Температура теплоносителя измеряется обычно вдоль поверхности

стенки F.

Теплопередача при переменных температурах зависит от взаимного направления движения теплоносителей. В непрерывных процессах теплообмена возможны следующие вариант направления движения жидкости относительно друг друга вдоль разделяющей их стенки:

1) параллельный ток, или прямоток, при котором теплоносители движутся в одном и том же направлении;

2) противоток, при котором теплоносители движутся в противоположном направлении;

3) перекрестный ток, при котором теплоносители движутся взаимно перпендикулярно друг другу;

4) смешанный ток, при котором один из теплоносителей движется в одном направлении, а другой – как прямоток, так и противотоком к первому. При этом различают простой, или однократный, смешанный ток и многократный смешанный ток.

а – прямоток; б – противоток; в – перекрестный ток;

г – однократный смешанный ток;

д – многократный смешанный ток.

Движущая сила процессов теплопередачи при переменных температурах изменяется в зависимости от вида взаимного направления движения теплоносителей. Поэтому выражение средней движущей силы или среднего температурного напора зависит от относительного направления движения теплоносителей и характера организации процесса теплопередачи (непрерывный или периодический).

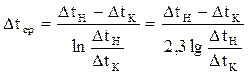
При отношении разности температур теплоносителей на концах теплообменника (Δt_Н/Δt_К) < 2, для технических расчетов применяют формулу:

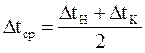
Уравнение теплопередачи при прямотоке:

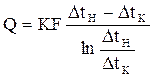
Изменение температуры при прямотоке

По заданной тепловой нагрузке Q и известным начальным и конечным температуре определяется основная расчетная величина – поверхность теплообмена.

При противотоке уравнение примет вид:

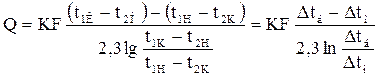
Величина Δt_б представляет собой разность температур на том конце теплообменника, где она больше;

Δt_м – меньшая разность температур на противоположном конце теплообменника.

Изменение температуры при противотоке

Средняя движущая сила при перекрестном и смешанном токе находят исходя из среднелогарифмический разности температур при противотоке

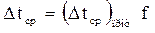
где f – поправочный множитель, меньше единицы.

Сравнение прямотока и противотока теплоносителей

При противотоке уменьшение расхода холодного теплоносителя уменьшение средней разности температур и как следствие увеличение рабочей поверхности.