Дифференциальные уравнения движения Навье – Стокса

При движении реальной (вязкой) жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения.

Действе сил трения Т на выделенный в потоке вязкой жидкости элементарный параллелепипед проявляется в возникновении на его поверхности касательных напряжений. Рассмотрим первоначально простой случай одномерного плоского потока капельной жидкости в направлении оси х, когда проекция скорости капельной жидкости в направлении оси х, когда проекция скорости ω_х зависит только от расстояния z до горизонтальной плоскости отсчета.

В этих условиях касательные напряжения возникают лишь на поверхностях dF верхней и нежней граней элементарного параллелепипеда, причем dF = dxdy. Если касательное напряжение на нижней грани параллелепипеда равно τ, то на верхней оно составит .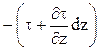

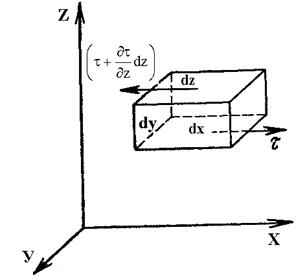При этом направления касательных напряжений на нижней и верхней гранях обусловлены, например, тем, что более медленные вышележащие слои жидкости затормаживают слой, в котором находится параллелепипед, а более быстрые нижележащие слои «разгоняют» его. Производная 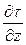выражает изменение касательного напряжения вдоль оси z в точках, лежащих на нижней грани параллелепипеда, а 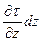представляет собой изменение этого напряжения вдоль всей длины dz ребра параллелепипеда.

Тогда проекция равнодействующей сил трения на ось х

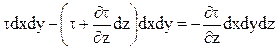
В общем случае проекция равнодействующей сил трения на ось х примет вид

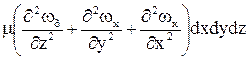
Сумму вторых производных по осям координат называют оператором Лапласа:

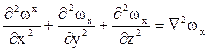
Следовательно

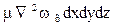
Соответственно проекции равнодействующей сил трения:

на ось у

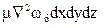
на ось х

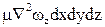
Проекции на оси координат равнодействующей всех сил (тяжести, давления и трения), действующих на элементарный объем капельной жидкости (с учетом проекций сил тяжести и давления, полученных при выводе уравнений Эйлера), составляют:

на ось х

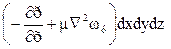
на ось у

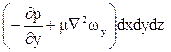
на ось z

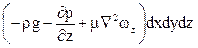
Согласно основного принципа динамики (сумма проекций сил на оси координат равны произведению массы жидкости 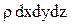на проекции ускорения на оси координат).

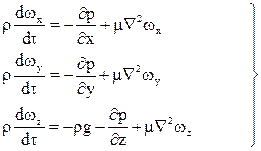(1)

Уравнения (1) представляют собой уравнения Навье – Стокса, описывающие движение вязкой капельной жидкости.

Уравнения Пуазейля – ламинарное установившееся.

Уравнение Бернулли

Решение уравнений движения Эйлера для установившегося потока приводит к одному из наиболее важных и широко используемых уравнений гидродинамики – уравнению Бернулли.

Для двух поперечных сечений 1 и 2 потока

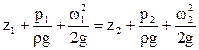(1)

Уравнение Бернулли для идеальной жидкости.

1 – называют полным гидродинамическим напором.

Следовательно, согласно уравнению Бернулли, для всех поперечных сечений установившегося потока идеальной жидкости величина гидродинамического напора остается неизменной.

z – нивелирная высота, называемая также геометрическим напором, представляет собой удельную потенциальную энергию положения в данной точке.

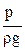– статический или пьезометрический напор, характеризует удельную потенциальную энергию давления в данной точке.

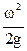– скоростной или динамический напор, характеризует удельную кинетическую энергию в данной точке.

Уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока.

Уравнение Бернулли реальных жидкостей

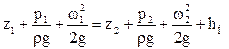
где h_П – потерянный напор, характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.