Осаждение частиц по действием силы тяжести

Рассмотрим движение тела в жидкости на примере осаждения твёрдой частицы в неподвижной среде под действием силы тяжести. Если частица массой m (и весом mg) начинает падать под действием силы собственного веса, то скорость её движения первоначально возрастает со временем. При полном отсутствии сопротивления среды скорость ω менялась бы во времени по известному закону ω = gτ. Однако с увеличением скорости будет расти, согласно уравнению 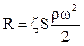, сопротивление движению частицы и соответственно уменьшаться её ускорение. В результате через короткий промежуток времени наступает динамическое равновесие: сила тяжести, под действием которой частица движется, станет равна силе сопротивления среды. Начиная с этого момента, ускорение движения будет равно нулю и частица станет двигаться равномерно с постоянной скоростью – скоростью осаждения ω_ос.

Сила, движущая шарообразную частицу диаметром d, выражается разностью между её весом и выталкивающей архимедовой силой, равной весу жидкости (среды) в объеме частицы:

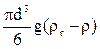
Сила сопротивления среды: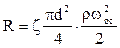

Скорость осаждения можно найти из уравнения равенства силы, движущей частицу, и силы сопротивления среды:

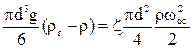
откуда 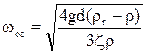(1)

Для ламинарной области: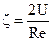

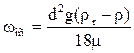
Отсюда можно найти максимальный размер частиц, осаждение которых происходит по закону Стокса.

Для этого Re = 2 ;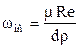

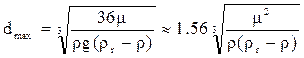
В случае переходной области 2 < Re < 500 получаем:

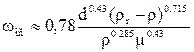
Аналогично для автомодельной области Re > 500 получаем:

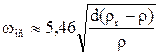
Для того чтобы выбрать одно из расчетных уравнений необходимо знать значение критерия Re, а туда входит значение ω_ос . Поэтому расчет ω_ос по приведенным выше уравнениям возможен только методом последовательных приближений. Вследствие трудоёмкости метода последовательных приближений удобно для определения ω_ос использовать метод предложенный Лященко П.В. Этот метод основан на преобразовании уравнения (1) путем подстановки в него скорости осаждения, выраженной через Re и возведения обоих частей уравнения в квадрат.

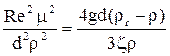
отсюда

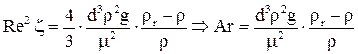
таким образом: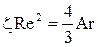

Для ламинарной области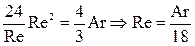

Предельное значение Ar для этой области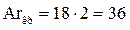

Для переходного режима 2 < Re < 500

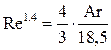предельное значение Ar = 83 000

Для автомодельной области Re > 500

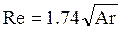
Скорость осаждения частицы не шарообразной формы меньше, чем скорость осаждения шарообразных частиц.

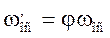
где φ – коэффициент формы.

Для угловатых частиц φ ≈ 0,66 , для продолговатых φ ≈ 0,58 (свободное и стесненное осаждение).