Дифференциальные уравнения движения Эйлера

Рассмотрим установившийся поток идеальной жидкости, движущейся без трения. Выделим в потоке элементарный параллелепипед объемом dV=dxdydz, ориентированный относительно осей координат.

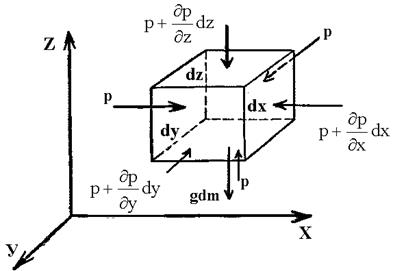Сила тяжести действующая на параллелепипед выражается произведением его массы dm на ускорение свободного падения g т.е. равна gdm.

р – сила гидростатического давления.

Основной принцип статики: сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю.

Проекции на оси координат сил тяжести и давления составит:

на оси х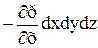

на оси y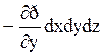

на оси z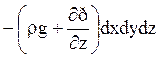

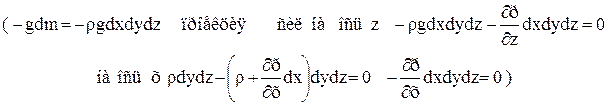
Согласно основному принципу динамики, сумма проекций сил, действующих на движущейся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение.

Масса жидкости в рассмотренном объеме dm = ρdxdydz

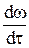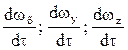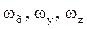Если жидкость движется со скоростью ω, то ее ускорение равно , а проекции ускорения на оси координат: где - составляющие скорости вдоль осей x, y, z.

В соответствии со основным принципом динамики:

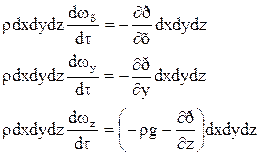
или после сокращения

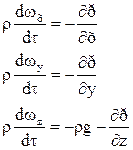(1)

или согласно субстанциональным производным соответствующих составляющих скорости получим.

Субстанциональная производная характеризует изменение какого-либо параметра или свойства материи (субстанции) во времени при перемещении материальных частиц в пространстве.

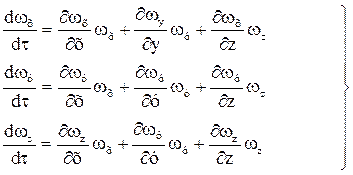(2)

Система уравнений (1) с учетом выражений (2) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для установившегося потока.

При неустановившемся движении скорость жидкости изменяется не только при перемещении частицы потока из одной точки пространства в другую, но и с течением времени в каждой точке.

Тогда для неустановившихся условий имеем:

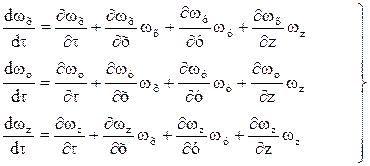(3)

Система уравнений (1) с учетом выражений (3) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для неустановившегося потока.

Интегралом уравнений движения Эйлера для установившегося потока является уравнение Бернулли.