Сложное вращение твердого тела вокруг параллельных осей.
Если оси вращательных движений тела параллельны, то вектор результирующей угловой скорости тела в неподвижной системе координат, определяемый согласно 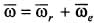 , будет колпинеарен векторам ее составляющих
, будет колпинеарен векторам ее составляющих 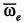 и
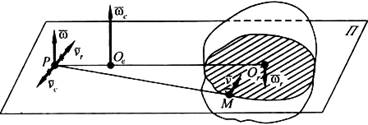
и 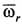 . Положение мгновенной оси вращения тела как оси, проходящей через неподвижную в данный момент точку Р тела, т. е. точку его МЦС в плоскости П, перпендикулярной осям вращений (рис. 7.3), можно определить из следующего анализа.
. Положение мгновенной оси вращения тела как оси, проходящей через неподвижную в данный момент точку Р тела, т. е. точку его МЦС в плоскости П, перпендикулярной осям вращений (рис. 7.3), можно определить из следующего анализа.
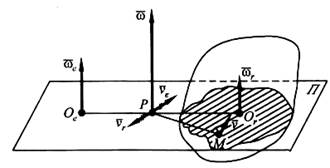
Относительная скорость точки Р 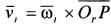 , а переносная
, а переносная 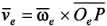 . Здесь Оr и Ое — точки пересечения плоскости П с соответствующими осями вращения. Тогда скорость точки Р в неподвижной системе координат
. Здесь Оr и Ое — точки пересечения плоскости П с соответствующими осями вращения. Тогда скорость точки Р в неподвижной системе координат 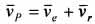 , причем, согласно определению МЦС, vP = 0 . Отсюда следует
, причем, согласно определению МЦС, vP = 0 . Отсюда следует 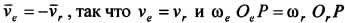 . В зависимости от взаимного расположения и численного значения векторов
. В зависимости от взаимного расположения и численного значения векторов 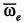 и
и 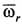 можно выделить три случая сложения вращательных движений.
можно выделить три случая сложения вращательных движений.
1) При совпадении направлений векторов 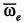 и
и 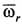 абсолютное движение будет плоским.
абсолютное движение будет плоским.
Абсолютная угловая скорость в этом случае будет иметь направление, совпадающее с направлениями ее составляющих, а ее модуль 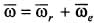 . Точка Р, через которую проходит мгновенная ось вращения тела, лежит на отрезке, соединяющем точки Оr и Ое. При этом
. Точка Р, через которую проходит мгновенная ось вращения тела, лежит на отрезке, соединяющем точки Оr и Ое. При этом 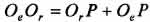 и положение точки Р можно найти из пропорции:
и положение точки Р можно найти из пропорции: 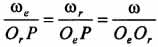 . Скорость любой точки тела, например M, в данном случае может быть найдена по формуле
. Скорость любой точки тела, например M, в данном случае может быть найдена по формуле 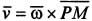 , а ее модуль
, а ее модуль 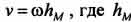 — кратчайшее расстояние от точки до мгновенной оси вращения, проходящей через точку Р.
— кратчайшее расстояние от точки до мгновенной оси вращения, проходящей через точку Р.
2) При противоположных направлениях векторов 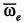 и
и 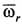 , когда
, когда 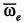 не равно
не равно 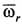 , абсолютное движение, как и в первом случае, будет плоским.
, абсолютное движение, как и в первом случае, будет плоским.
Абсолютная угловая скорость при этом будет иметь направление, совпадающее с направлением большей по модулю составляющей угловой скорости, а ее модуль 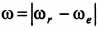 .
.
Точка P, через которую проходит мгновенная ось вращения тела, лежит в плоскости П, перпендикулярной осям вращательных движений, на прямой, проходящей через точки Ое и Ог; расположена она внешним образом по отношению к этим точкам со стороны той точки, через которую проходит ось вращения движения с большей угловой скоростью. При этом 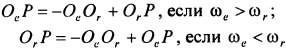 . Пропорции для нахождения положения точки Р имеют вид
. Пропорции для нахождения положения точки Р имеют вид 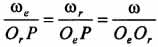
3) При противоположных направлениях векторов омега переносное и омега радиальное и равенство их модулей, если условие  выполняется на отрезке времени t2-t1, абсолютное движение будет поступательным. Такой случай сложения вращательных движений называется парой вращений.
выполняется на отрезке времени t2-t1, абсолютное движение будет поступательным. Такой случай сложения вращательных движений называется парой вращений.

Пара вращений.
При противоположных направлениях векторов омега переносное и омега радиальное и равенство их модулей, если условие  выполняется на отрезке времени t2-t1, абсолютное движение будет поступательным. Такой случай сложения вращательных движений называется парой вращений.
выполняется на отрезке времени t2-t1, абсолютное движение будет поступательным. Такой случай сложения вращательных движений называется парой вращений.

Аксиомы статики.
1) Если на свободное твердое тело действует две силы, то тело может находиться в равновесии только тогда, когда эти силы равны по модулю, действуют по одной прямой в противоположные стороные.
2) Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней добавить или от нее отнять уравновешенную систему сил.
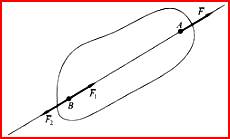
Следствие. Не изменяя действия силы на абсолютно твердое тело, силу можно переносить по линии ее действия в любую точку тела.
3) При всяком действии одного материального тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению.
Следствие. Сумма всех внутренних сил всегда равна нулю.
4) Две силы, приложенные к твердому телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах как на сторонах.
5) Механическое состояние системы не изменится, если освободить ее от связей, приложив к точкам системы силы, равные реакциям связей.
Материальные тела, ограничивающие перемещение данного тела в пространстве, называют связями.
Сила, с которой связь действует на тело, препятствуя его перемещениям, называется силой реакции связи, или просто реакцией связи.
Дата добавления: 2018-11-26; просмотров: 977;











