Пара сил. Теорема о сумме моментов сил, составляющих пару, относительно произвольной точки.

Пара сил - система двух сил равных по модулю и противоположных по направлению.

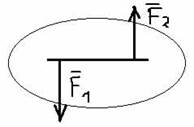
F1 = -F2

R* = F1 - F2 = 0

AC/F2 = BC/(R*) (стремится к бесконечности)

(F1,F2) не эквивалентны 0

Момент пары сил - произведение одной из сил на ее плечо.

M(F1,F2) = M12 = ±F1*d = ±F2*d

Векторный момент пары сил.

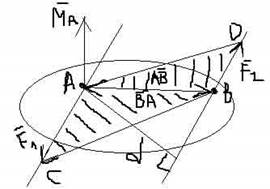
MA = AB * F2

MA = F2 * AB * sinα = F2d

MB = BA * F1 = F1 * d

M = MA = MB = S(ACBD)

Теорема о сумме моментов сил, составляющих пару, относительно произвольной точки:Сумма моментов сил, входящих в состав пары сил относительно любой точки не зависит от ее выбора и равна моменту этой пары сил.

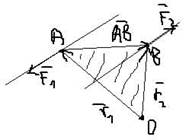
F1 = -F2

Mo(F2) + Mo(F1) = r2*F2 + r1*F1 = r2*F2 - r1*F2 = (r2 - r1)*F2 = AB * F2 = M(F1,F2)

Векторный и алгебраический моменты пары сил.

Алгебраический момент M=±F•d (пара). M=±dF1=±dF2=±2SΔABC= ±S. Он не меняется при перемещении сил вдоль линии их действия (ни плечо, ни направление вращения не меняются).

Векторный момент – вектор M=M(F,F’), направлен перпендикулярно плоскости пары в ту сторону, откуда видно стремление пары повернуть тело против часовой хода стрелки, его модуль равен алгебраическому моменту пары.
M(F1,F2)=BAxF1=ABxF2.

Дополнение:

( + 32) Момент силы относительно оси )