Скорости и ускорения точек тела при его вращении вокруг неподвижной точки.

Скорости и ускорения точек твердого тела при его свободном движении.

Переносное движение - поступательное движение вместе с полюсом. (Ve)

Относительное движение - вращательное движение относительно полюса. (Vr)

ρ = r0 + r

vM = dρ/dt = dr0/dt + dr/dt = v0 + ωr = (vM)e + (vM)r

a = dv/dt = dv0/dt + (dω/dt)*r + ω(dr/dt) = a0 + ε*r+ ω*r = a0 + a(вр) + а(ос) = (аМ)е + (аМ)r

(все что идет ниже, может не относиться к этому вопросу)

Докажем,

v = v0 + ω*r

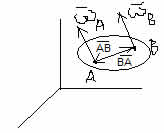
1) Полюс - т. А: vB = vA + ωS*AB

2) Полюс - т. В: vA = vB + ωB*BA = vB - ωB*AB

1) + 2) : (vB + vA) = (vA + vB) + ω*AB- ωB*AB

(ωA - ωB)*AB = 0

Сложное движение точки. Основные понятия.

Движение точки, исследуемое одновременно в основной и подвижной (подвижных) системах отсчета, называется сложным. В простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения.

Рассмотрим сложное движение точки M, перемещающейся по отношению к подвижной системе O'XYZ, связанной с некоторым телом Qy которое в свою очередь совершает свободное движение по отношению к основной, условно неподвижной системе Oxyz.

Движение точки М по отношению к неподвижной системе отсчета Oxyz называется абсолютным, или сложным, состоящим из относительного движения по отношению к подвижной системе O'XYZ и переносного — движения подвижной системы отсчета O'XYZ по отношению к неподвижной системе Oxyz.

Положение точки М в подвижной системе координат O'XYZ характеризует радиус-вектор 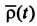с началом в точке О'. Траектория точки М в подвижной системе отсчета называетсяотносительной траекторией и представляет собой годограф радиус-вектора 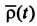. Скорость движения точки М по отношению к осям подвижной системы координат называется относительной скоростью и обозначается Vr. Вектор Vr определяет скорость изменения с течением времени радиус-вектора 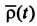в подвижной системе O'XYZ и поэтому выражается его относительной, или локальной, производной по времени, .
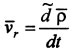Ускорение точки М в этом движении называется относительным ускорением и обозначается аr. Вектор аr характеризует скорость изменения вектора относительной скорости Vr в подвижной системе O'XYZ и поэтому выражается относительной, или локальной, производной по времени от Vr: .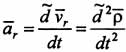

Движение подвижной системы O'XYZ по отношению к неподвижной Oxyz является для точки М переносным движением, а скорость и ускорение той неизменно связанной с подвижной
системой отсчета точки А, с которой в данный момент времени совпадает точка М, называют переносными скоростью и ускорением точки М и обозначают Ve и ае.

Переносные скорость и ускорение точки М определяются по формулам: 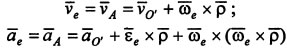, где вектора Vo' и ao' - скорость и ускорение точки О' подвижной системы координат.