Линейные однородные дифференциальные уравнения
Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида
 .
.
Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.
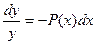
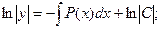
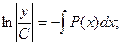
Общее решение: 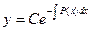
Линейные неоднородные дифференциальные уравнения
Для интегрирования линейных неоднородных уравнений (Q(x)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.
Метод Бернулли
Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций 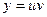 .
.
При этом очевидно, что 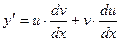 - дифференцирование по частям.
- дифференцирование по частям.
Подставляя в исходное уравнение, получаем:
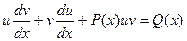
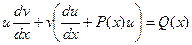
Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.
Например, функция 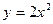 может быть представлена как
может быть представлена как 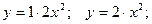
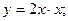 и т.п.
и т.п.
Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение 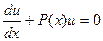 .
.
Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:
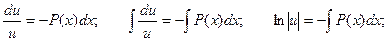
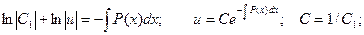
Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение 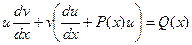 с учетом того, что выражение, стоящее в скобках, равно нулю.
с учетом того, что выражение, стоящее в скобках, равно нулю.
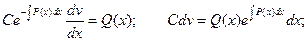
Интегрируя, можем найти функцию v:
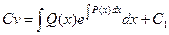 ;
; 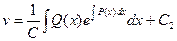 ;
;
Т.е. была получена вторая составляющая произведения 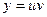 , которое и определяет искомую функцию.
, которое и определяет искомую функцию.
Подставляя полученные значения, получаем:
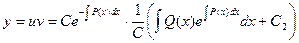
Окончательно получаем формулу:
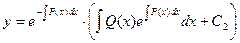 ,
,
где С2 - произвольный коэффициент.
Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.
Метод Лагранжа
Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной.
Вернемся к поставленной задаче:
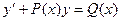
Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.
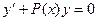
Далее находится решение получившегося однородного дифференциального уравнения:
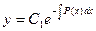 .
.
Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С1 некоторой функцией от х.
Тогда по правилам дифференцирования произведения функций получаем:
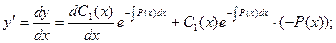
Дата добавления: 2020-06-09; просмотров: 539;











