Приближенные вычисления с помощью дифференциала
1. Вычисление приближенного значения приращения функции
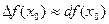
Пример. Пользуясь понятием дифференциала функции, вычислить приближенно изменение функции 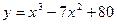 при изменении аргумента от 5 до 5,01.
при изменении аргумента от 5 до 5,01.
Найдем дифференциал функции 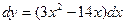 . Подставим значения х0 = 5, Dх = 0,01. Получим
. Подставим значения х0 = 5, Dх = 0,01. Получим 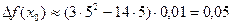
2. Вычисление приближенного значения функции
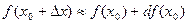
Пример. Вычислить приближенное значение с помощью дифференциала 1,9985.
Рассмотрим функцию 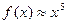 , где х = 1,998. Разобьем х на х0 и Dх (х = х0 + Dх), пусть х0 = 2, тогда Dх = - 0,002.
, где х = 1,998. Разобьем х на х0 и Dх (х = х0 + Dх), пусть х0 = 2, тогда Dх = - 0,002.
Найдем значение 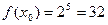 ,
, 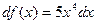 ,
, 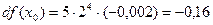
Тогда 1,9985 » 32 – 0,16 = 31, 84.
Производные и дифференциалы высших порядков
Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
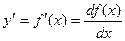
Если найти производную функции f¢(x), получим вторую производнуюфункции f(x).
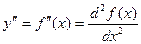
т.е. y¢¢ = (y¢)¢ или 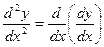 .
.
Этот процесс можно продолжить и далее, находя производные степени n.
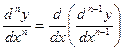 .
.
Основные теоремы дифференциального исчисления
1. Теорема Ролля. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то в интервале (а, b) существует хотя бы одна точка c (a < c < b), в которой производная f '(с) = 0.
Геометрический смысл теоремы Роля. Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка с такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.
Заметим, что если хотя бы в одной точке промежутка [a; b] функция не дифференцируема, то производная функции f (x) может в нуль и не обратиться. Например, функция y =1-½x½непрерывна на промежутке [-1; +1], дифференцируема в (-1;+1) за исключением точки x0 = 0, причем f (-1) = f (1) = 0, т.е. условие теоремы Ролля нарушено в единственной точке x0 = 0 (в ней функция не дифференцируется). Очевидно, что ни в одной точке графика функции на промежутке [-1; 1] касательная к графику не параллельна оси 0x.
Теорема Ролля имеет несколько следствий:
1) Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем f(a) = f(b) = 0, то существует, по крайней мере, одна точка с, a < с < b, такая, что f¢(с) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.
2) Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)-го порядка и n раз обращается в нуль, то существует, по крайней мере, одна точка интервала, в котором производная (n –1)–го порядка равна нулю.
2. Теорема Лагранжа. Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (а, b), то в этом интервале найдется, по крайней мере, одна точка c (a < c < b), такая, что 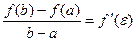 .
.
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа.
Выражение 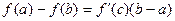 называется формулой конечных приращений Лагранжа.
называется формулой конечных приращений Лагранжа.
Геометрический смысл теоремы Лагранжа.
Пусть выполнены условия теоремы Лагранжа, тогда справедлива формула конечных приращений Лагранжа.
Пусть точки A и B, лежащие на графике функции, имеют координаты A (a; f (a)), B (b; f (b)), тогда очевидно, что величина дроби 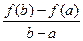 равна тангенсу угла наклона хорды AB к оси Оx, т.е.
равна тангенсу угла наклона хорды AB к оси Оx, т.е. 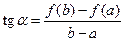 .
.
С другой стороны, f '(c) = tga. Значит, в точке x = c касательная к графику функции y = f (x) параллельна хорде, стягивающей дугу кривой AB. В этом и заключается геометрический смысл теоремы Лагранжа.
3. Теорема Коши. Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы в интервале (a, b) и g¢(x) ¹ 0 ни в одной точке этого интервала, то существует по крайней мере одна точка c (a < c < b), такая, что имеет место равенство:
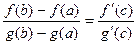 .
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке с.
Геометрический смысл теоремы Коши.
Нетрудно убедиться в том, что геометрический смысл теоремы Коши совпадает с геометрическим смыслом теоремы Лагранжа.
Дата добавления: 2020-06-09; просмотров: 785;











