Уравнение прямой, проходящей через две точки
Пусть на плоскости заданы две точки M1(x1, y1) и M2(x2, y2), тогда уравнение прямой, проходящей через эти точки имеет вид:
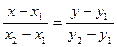
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Применяя записанную выше формулу, получаем:
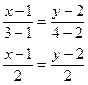
Уравнение прямой по точке и угловому коэффициенту
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
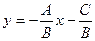
и обозначить 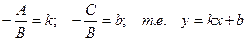 , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
, то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
Уравнение прямой в отрезках
Если в общем уравнении прямой Ах + Ву + С = 0 коэффициент С ¹ 0, то, разделив на С, получим: 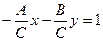 или
или
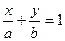 , где
, где 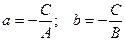
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1, 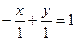 , а = -1, b = 1.
, а = -1, b = 1.
Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Уравнение прямой имеет вид: 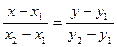 , где х1 = у1 = 0; x2 = -2; y2 = -3.
, где х1 = у1 = 0; x2 = -2; y2 = -3.
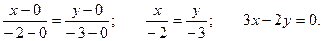
Дата добавления: 2020-06-09; просмотров: 942;











