Действия над векторами, заданными своими координатами
Действия над векторами
1. Суммой двух векторов называется вектор 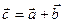 , удовлетворяющий условию: если начало вектора
, удовлетворяющий условию: если начало вектора 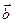 перенести в точку, являющуюся концом вектора
перенести в точку, являющуюся концом вектора  , начало вектора
, начало вектора 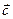 совпадет с началом вектора
совпадет с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора 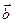 (правило треугольника).
(правило треугольника).
2. Произведением вектора  на число a называется вектор
на число a называется вектор 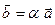 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) 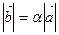 ;
;
2) вектор 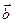 коллинеарен вектору
коллинеарен вектору  ;
;
3) вектор  соноправлен с вектором
соноправлен с вектором 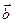 (
( 
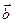 ), если a > 0 и противоположно направлен (
), если a > 0 и противоположно направлен (  ¯
¯ 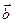 ), если a < 0.
), если a < 0.
Свойства векторов
1)  +
+ 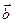 =
= 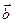 +
+  - коммутативность.
- коммутативность.
2)  + (
+ ( 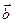 +
+ 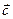 ) = (
) = (  +
+ 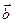 )+
)+ 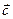
3)  +
+ 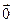 =
= 
4)  +(-1)
+(-1)  =
= 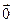
5) (a×b)  = a(b
= a(b  ) – ассоциативность
) – ассоциативность
6) (a+b)  = a
= a  + b
+ b  - дистрибутивность
- дистрибутивность
7) a(  +
+ 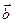 ) = a
) = a  + a
+ a 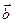
8) 1×  =
= 
Координаты вектора
Пусть точки А(х1, y1) и B(x2, y2), заданы в прямоугольной декартовой системе координат.
Чтобы найти координаты вектора 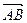 нужно из координат его конца вычесть координаты начала т.е.
нужно из координат его конца вычесть координаты начала т.е. 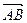 = (x2 – x1, y2 – y1).
= (x2 – x1, y2 – y1).
Действия над векторами, заданными своими координатами
Если векторы заданы в прямоугольной декартовой системе координат своими координатами, то
1) при сложении двух и большего числа векторов их одноименные координаты складываются, т.е. если 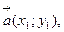
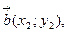 то
то 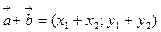 ;
;
2) при вычитании векторов их одноименные координаты вычитаются, т.е. если 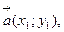
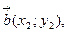 то
то 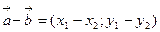 ;
;
3) при умножении вектора на число каждая координата вектора умножается на это число, т.е. если 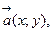 то
то 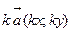
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки на плоскости А(х1; y1), B(x2; y2), то
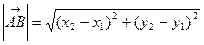 .
.
Если точка М(х; у) делит отрезок АВ в соотношении l/m, то координаты этой точки определяются как:
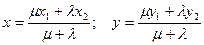
В частном случае координаты середины отрезка находятся как:
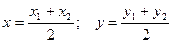
Дата добавления: 2020-06-09; просмотров: 1844;











