ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Тема 2.1. Матрицы и определители
Матрицейразмера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А = 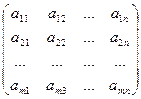
Часто вместо подробной записи употребляют сокращенную: 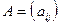 .
.
Виды матриц
Если число строк матрицы равно числу ее столбцов (m = n), то матрица называется квадратной.
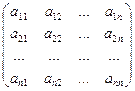
Число строк или число столбцов квадратной матрицы называется ее порядком.
Диагональ 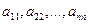 квадратной матрицы называется главной диагональю, а диагональ
квадратной матрицы называется главной диагональю, а диагональ 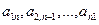 – побочной диагональю.
– побочной диагональю.
Квадратная матрица называется треугольной, если все ее элементы, которые находятся ниже (или выше) главной диагонали, равны нулю, т.е. треугольная матрица имеет вид:
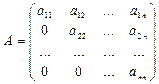 или
или 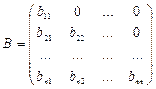 .
.
При этом матрицу 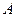 называют верхнетреугольной, а матрицу
называют верхнетреугольной, а матрицу 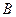 – нижнетреугольной.
– нижнетреугольной.
Квадратная матрица, у которой отличны от нуля только элементы, расположенные на главной диагонали, называется диагональнойматрицей.
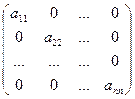
Среди квадратных матриц важную роль играет матрица вида:
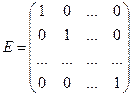 ,
,
которая называется единичной. Для любой квадратной матрицы А имеют место равенства: АЕ = ЕА = А
Если amn = anm , то матрица называется симметрической.
Пример. 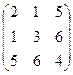 - симметрическая матрица
- симметрическая матрица
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается:
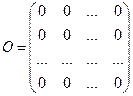
Равенство матриц
Две матрицы 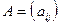 и
и 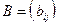 называются равными, если совпадают их размеры и
называются равными, если совпадают их размеры и 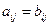 при любых
при любых 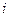 и
и 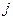 .
.
Дата добавления: 2020-06-09; просмотров: 710;











