Основы теории подобия лопаточных насосов.

Используемые при проектировании лопаточных насосов расчетные методы не позволяют с достаточной степенью точности учитывать множество факторов, влияющих на характеристику насоса. Поэтому после изготовления и испытания опытного образца, как правило, возникает необходимость доработки ряда конструктивных параметров. При проектировании крупногабаритных насосов экспериментальная доводка является не только трудоемкой, но и дорогостоящей. Более простой путь к достижению конечной цели – изготовление новой конструкции насоса в виде его уменьшенной копии – модели натурного объекта. Но для того чтобы перейти от модели к натурному образцу и наоборот необходимо знать методику такого перехода и формулы перехода. В основе этого метода лежат общие законы гидродинамического подобия.

Из курса гидравлики известно, что модель и натура какого-либо объекта подобны, если они подобны в геометрическом, кинематическом и динамическом отношениях.

Геометрическое подобие насоса заключается в том, что соотношение сходственных линейных размеров деталей насоса натуры и модели характеризуется одним и тем же масштабным коэффициентом к_l и соблюдается равенство соответствующих конструктивных углов лопаток и углов конфузора и диффузора:

к_l= 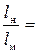const.;

β_1н= β_1м=β₁; β_2н= β_2м=β₂;

φ_кн= φ_км= φ_к; φ_дн= φ_дм= φ_д.

У геометрически подобных насосов планы скоростей в соответствующих сечениях будут подобны. На основании этого можно составить следующее соотношение компонентов плана скоростей для насоса натуры и модели, то есть записать условие кинематического подобия:

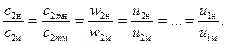(51)

Соотношение для окружных скоростей можно представить в виде:

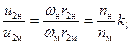, (52)

где к_l – линейный масштабный коэффициент.

Критерием гидродинамического подобия насосов является критерий Рейнольдса, поскольку основными силами являются силы вязкостного трения. У гидродинамически подобных насосов движение жидкости в сходственных сечениях насоса натуры и модели должно характеризоваться одинаковыми числами Рейнольдса. Это условие можно записать следующим образом:

R_eiн= R_eiм= 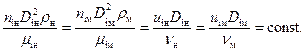, (53)

где i – номер сечения у насоса натуры и модели; μ – динамическая вязкость жидкости, μ=ν·ρ; ν – кинематическая вязкость; ρ – плотность жидкости.

Применим приведенные отношения к конкретным параметрам насоса. Теоретическую подачу насоса, например, для выходного сечения колеса можно представить в виде: Q_т=2πr₂b₂c_2m.

Тогда отношение подач насоса натуры и модели запишется в виде:

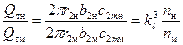. (54)

Если записать эти отношения для действительной подачи, то нужно учесть объемный к.п.д. насоса натуры 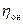и модели :

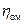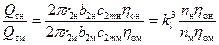. (54а)

Действительный напор насоса можно вычислить по формуле, с учетом гидравлических потерь: H=H_тη_г=к₁η_{г ,}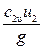

где η_г – гидравлический к.п.д. насоса.

Запишем отношение действительных напоров насоса натуры и модели:

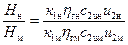. (55)

Принимая во внимание равенство коэффициентов к₁, учитывающих конечное число лопаток, и равенство гидравлических к.п.д., а так же уравнение (50), выражение (53) примет вид:

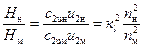. (56)

Составим соотношение для полезной мощности насоса натуры и модели:

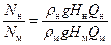. (57)

Принимая во внимание уравнение (56) для соотношения напоров и уравнение (54) для подач, выражение (57) примет вид:

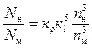, (57а)

где к_ρ=ρ_н/ρ_м – масштабный коэффициент плотности.

Таким образом, уравнения (54) – (57) объединяют основные параметры насоса натуры и модели и позволяют выполнять пересчет этих параметров, с насоса натуры на модель и обратно. В теории насосов эти уравнения называют общими формулами подобия. Если применить эти формулы к одному и тому же насосу, то линейный масштабный коэффициент к_l будет равен единице, отношение коэффициентов, учитывающих конечное число лопаток так же будет равно единице и уравнения (54) – (57) упрощаются и используются для пересчета основных параметров работы насоса при изменении частоты вращения рабочего колеса. Применительно к указанному случаю эти уравнения примут вид:

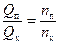. (58)

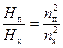. (59)

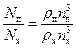. (60)

Индексом «п» в уравнениях (58) – (60) обозначены параметры насоса в соответствии с паспортными данными, а индексом «х» те же параметры при числе оборотов колеса отличном от паспортных. Уравнения (58) – (60) получили название частные формулы подобия.