Критерии принятия решений в условиях полной неопределенности

Если известны законы распределения доходности финансовой операции развивающейся в той или иной экономической ситуации, или хотя бы вероятности различных возможных исходов данной финансовой операции, то инвестор при принятии решения может руководствоваться вероятностными показателями, описанными в п. 3.2.

Но ситуация может быть полностью неопределенной, то есть не известны ни вероятности различных исходов финансовой операции ни, тем более, закон распределения доходности финансовой операции. В данных условиях полной неопределенности инвестор или лицо принимающее решение может только предположить возможные варианты развития экономической ситуации при ее совершении.

Предположим, что число возможных ситуаций конечно и равно L. В каждой предполагаемой j-той ситуации 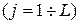лицо принимающее решение (ЛПР) – инвестор может принять N финансовых решений. В случае принятия i-того финансового решения 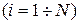могут быть рассчитаны доходности финансовой операции 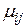при принятии i-того решения в j-той экономической ситуации. Эти возможности значения доходности 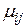образуют матрицу доходностей.

	j i				¼	L	(3.27)
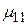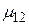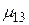					¼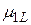
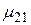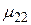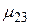					¼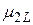
M =		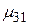		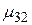	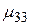¼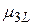
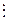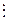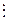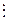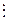	N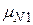

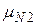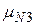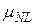Предположим, инвестором предполагается три возможных варианта развития ситуации L = 3. В каждой из возможных ситуаций ЛПР может принять по четыре решения N = 4. Анализ развития финансовой операции при принятии i-того решения в j-той экономической ситуации позволил определить все элементы матрицы доходностей.

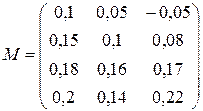(3.28)

Как было отмечено в п. 3.2 принимаемое решение в условиях неопределенности зависит от склонности ЛПР к риску. Поясним подходы к определению риска в данной ситуации полной неопределенности.

Определим величины риска, которые соответствуют принятию i-того решения в j-той ситуации - 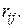Если бы ЛПР однозначно знало ситуацию, которая реально сложится при развитии финансовой операции, то выбрало бы решение, обеспечивающее максимальную доходность. Если реальная ситуация соответствовала бы j-той, то было бы принято решение обеспечивающее максимальную доходность:

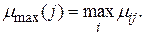(3.29)

При принятии любого i-того решения в j-той ситуации ЛПР рискует получить доходность не 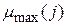, а только 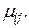При таком определении риски 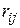логично определять разностью:

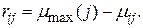(3.30)

Элементы 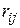, рассчитываемые по формуле (3.30), образуют матрицу рисков. Составим матрицу рисков, соответствующую матрице доходностей (3.28). Для максимальных доходностей 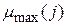в соответствии с (3.29) получим 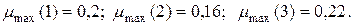В соответствии с (3.30) матрица рисков будет иметь вид:

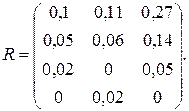(3.31)

По матрице доходностей (3.27) могут быть приняты финансовые решения, являющиеся оптимальными по тому или иному критерию. При принятии финансовых решений используют следующие критерии.

Правило Вальда

При принятии решения в соответствии с данным правилом предполагают, что будет иметь место самая неблагоприятная ситуация. В соответствии с данным предположением правило Вальда называют также правилом крайнего пессимизма. Самая неблагоприятная ситуация характеризуется самой малой доходностью:

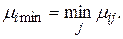(3.32)

В соответствии с матрицей доходности (3.28) по правилу (3.32) находим:

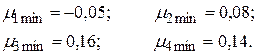
Правило Вальда рекомендует принять решение 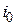с наибольшим значением 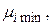то есть

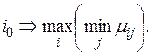(3.33)

В соответствии с правилом (3.33) оптимальным по правилу Вальда будет третье решение 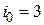с доходностью:

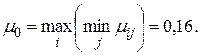
3.4.2. Правило "розового оптимизма"

В соответствии с этим правилом предполагается, что будет действовать самая благоприятная ситуация, которая при любом i-том решении обеспечит максимальную доходность:

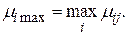(3.34)

В соответствии с матрицей доходности (3.28) по правилу (3.34) находим:

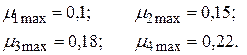
Оптимальным решением по правилу "розового оптимизма" является решение 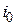, обеспечивающее максимальную доходность из всех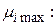

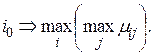(3.35)

Из приведенных значений 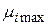видно, что по правилу "розового оптимизма" оптимальным решением будет четвертое решение 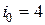с доходностью:

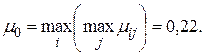
Правило Гурвица

По правилу Гурвица оптимальным считается решение 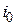, которое обеспечивает максимум взвешенной суммы доходностей пессимистического (3.33) и оптимистического (3.35) подходов:

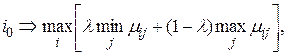(3.36)

где 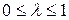- весовой коэффициент, значение которого выбирается лицом, принимающим решение из субъективных соображений.

При 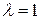правило Гурвица совпадает с правилом Вальда, а при 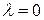- с правилом "розового оптимизма".

Вычислим значения:

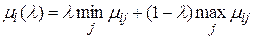(3.37)

для двух значений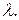

При 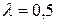получим следующие значения :

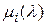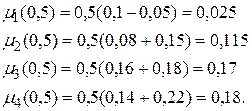
В соответствии с правилом (3.36) видно, что оптимальным является четвертое решение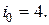

При 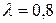получим следующие значения :

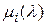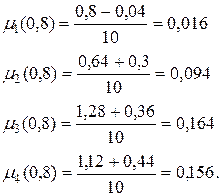
Из вычисленных значений 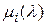видно, что при 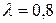оптимальным является третье решение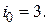

Правило Сэвиджа

Правило Сэвиджа называют также правилом минимального риска. При применении этого правила анализируется матрица рисков 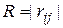и предполагается, что будет действовать ситуация максимального риска:

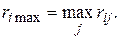(3.38)

В соответствии с правилом Сэвиджа оптимальным считается решение 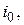при котором обеспечивается минимальное значение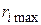

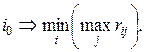(3.39)

По приведенным выше значениям элементов матрицы 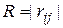(3.31) для 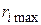в соответствии с (3.38) получим:

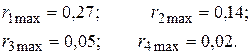
Из вышеперечисленных значений 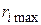и правила (3.39) следует, что оптимальным является четвертое решение 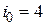при минимальном значении риска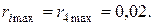

Тема 4. Портфельный анализ