Портфель максимальной эффективности при заданном его риске

Рассмотрим портфель состоящий из двух видов бумаг. Задача нахождения структуры портфеля 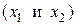, обеспечивающих его максимальную эффективность при заданном риске может быть записана в виде:

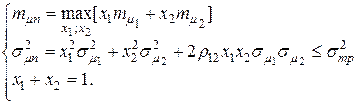(4.31)

Из второго уравнения (4.31) можно определить две пары значений 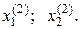Для этого сделаем замену переменной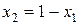

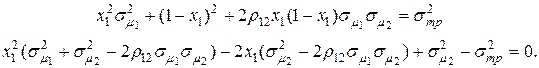
Из решения данного уравнения находим:

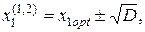(4.32)

где:

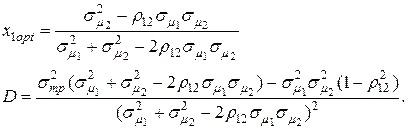(4.33)

Значения 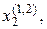находим из условия:

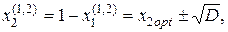
где 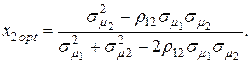(4.34)

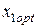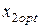При значениях и риск портфеля ценных бумаг будет минимальным (см. рис.____). При значениях ценовых долей бумаг первого и второго вида:

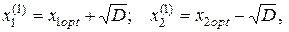(4.35)

а также при

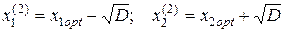(4.36)

риск портфеля ценных бумаг 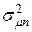будет равен заданному значению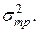

Второе неравенство в (4.31) будет выполняться, когда значения 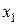и 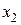будут соответствовать условиям:

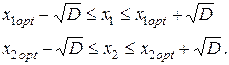
Из рис. ___ видно, что эффективность портфеля ценных бумаг двух видов 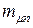изменяется линейно при изменении 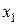от 0 до 1. Из этого следует, что в зависимости от соотношения значени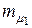й и 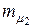портфель максимальной эффективности при заданном риске обеспечивается структуре портфеля, определяющейся формулами (4.35) или (4.36).

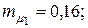
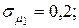
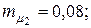
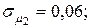
Пример 4.4. Портфель ценных бумаг состоит из двух видов коррелированных (зависимых) бумаг со следующими значениями эффективности и риска 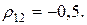Определить структуру портфеля ценных бумаг максимальной эффективности при заданном его риске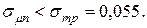

Решение. Определим значение 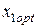и 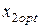, при которых обеспечивается минимальный риск портфеля ценных бумаг:

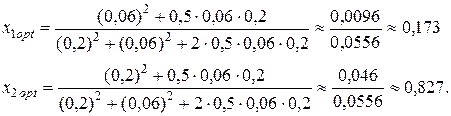
Определим минимальное значение риска портфеля ценных бумаг и его эффективность:

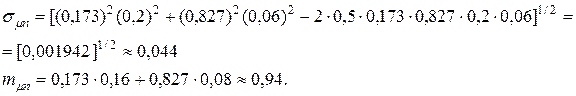
Определим значение дискриминанта D:

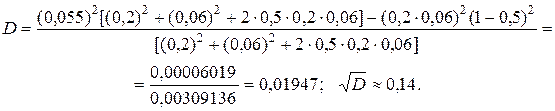
По формулам (4.35) и (4.36) определяем границы интервалов возможных значений ценовых долей бумаг:

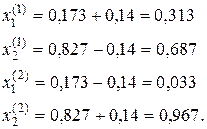
Определим риск и эффективность портфеля ценных бумаг пр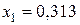и и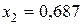

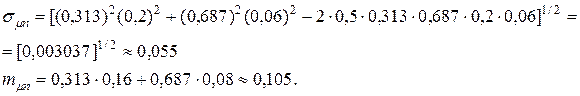
При ценовых долях бумаг 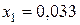и 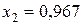для риска и эффективности портфеля ценных бумаг получим значение:

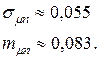
Из приведенных расчетов следует, что портфель максимальной эффективности при заданном риске обеспечивается при ценовых долях ценных бумаг равных 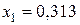и 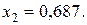При этом эффективность портфеля равна 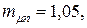а риск определяемый коэффициентом вариации будет равен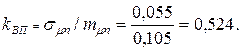

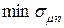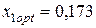Для оптимального портфеля по критерию минимума среднеквадратического отклонения доходности портфеля при и 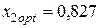эффективность портфеля равна 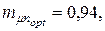а риски оцениваемые коэффициентом вариации равны 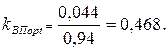Таким образом, переход от оптимального по 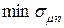портфеля к портфелю с максимальной эффективности увеличивает риски по коэффициенту вариации в 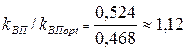раз. Но эффективность портфеля также возрастает 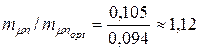раз.

* При 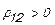не выполняются условия x₁>0; x₂>0 x₁+x₂=1.