Уравнение непрерывности

В общем случае концентрация носителей зависит от координаты и времени: n(x,t), p(x,t). Эти зависимости можно найти, решив урав­нение непрерывности, записываемое в виде:

для неосновных носителей в р-полупроводнике

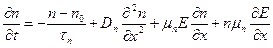(2.54)

для неосновных носителей в n-полупроводнике

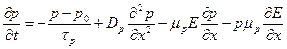(2.55)

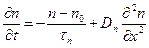(2.56)

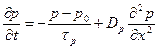(2.57)

Эти уравнения учитывают процесс диффузии и рекомбинации и называются уравнениями диффузии.

В полупроводниковых приборах часто рассматривается стацио­нарный режим, когда концентрации не изменяются во времени (dn/dt=0, dp/dt=0).

Рассмотрим p-полупроводник, в котором dn/dt=0. Тогда вместо (2.56) можно записать

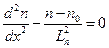(2.58)

где принято обозначение

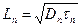(2.59)

Так как 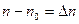– избыточная концентрация электронов, то вместо (2.58) запишем

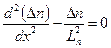(2.60)

Решением этого дифференциально­го уравнения второго порядка является сумма экспонент:

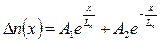(2.61)

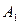а коэффициенты и 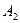определяются из граничных условий.

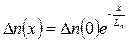(2.62)

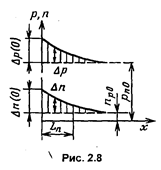
Из выражения (2.62) следует, что при 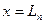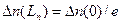. Характерную длину 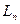, на которой избыточная концентрация электронов при диффузии уменьшается из-за рекомбинации в е =2,72 раза, называют диффузионной длиной электронов. При х > 3 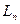уже можно считать, что 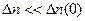, т.е. состояние счита­ется равновесным.

Аналогично (2.62) можно записать и закон изменения избыточ­ной концентрации дырок в n-полупроводнике:

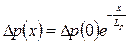(2.63)

где, как и в (2.59),

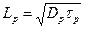(2.64)

– диффузионная длина дырок в n-полупроводнике.

ГЛАВА 3