Вольт-амперная характеристика идеализированного р-n-перехода

Идеализированным является р-n-переход, для которого приня­ты следующие допущения.

1. В обедненном слое отсутствует генерация, рекомбинация и рассеяние носителей зарядов, т.е. предполагается, что ток носите­лей заряда одного знака одинаков на обеих границах перехода.

2. Электрическое поле вне обедненного слоя отсутствует, т.е. полупроводник вне перехода остается электрически нейтральным и в нем носители могут совершать только диффузионное движение.

3. Электрическое сопротивление нейтральных р- и n-областей считается пренебрежимо малым по сравнению с сопротивлением обедненного слоя, т.е. все внешнее напряжение практически полно­стью приложено к обедненному слою.

4. Границы обедненного слоя считаются плоскопараллельными, а носители заряда перемещаются по направлению, перпендикуляр­ному к этим плоскостям. Концентрации носителей зависят только от одной координаты.

По определению (2.30) прирост концентрации неосновных носителей в области n (дырок), т.е. избыточная концентрация их,

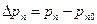(3.23)

Аналогично избыточная концентрация электронов – неосновных носителей в p-области при инжекции

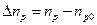(3.24)

на границе с p-областью

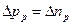(3.25)

на границе с n-областью

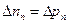(3.26)

(3.27) (3.28)

Теория р-n-перехода основана еще на одном важном предположении, что избыточные концентрации много меньше концентрации основных носителей:

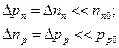
Связь для состояния равновесия может быть найдена из (3.9):

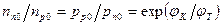(3.29)

Для неравновесного состояния вместо (3.29) следует писать

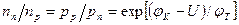(3.30)

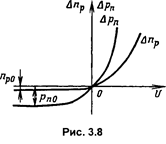Но так как 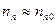, а 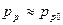, то получим

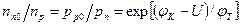(3.31)

Из (3.31) получим зависимость избыточных концентраций неосновных носителей от U при инжекции:

(3.32)

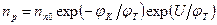
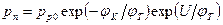
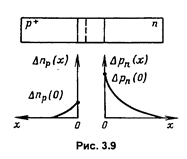Используя формулы (3.29) вместо (3.32) можно написать

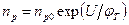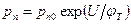, (3.33)

С учетом (3.33), (3.23) и (3.24) найдем избыточные концентрации неосновных но­сителей на границах перехода

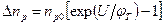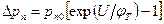, (3.34)

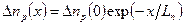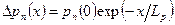, (3.35)

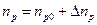и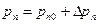

Следовательно,

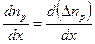и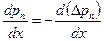

С учетом этого вместо формул (2.52) напишем

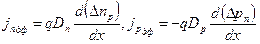(3.36)

Подставив результаты дифференцирования (3.35) в формулы (3.36), получим значение плотности токов в любом сечении х:

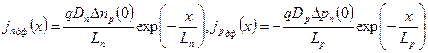(3.37)

Плотность диффузионного тока убывает по направлению (от границы перехода) и при х = 0 имеет максимальное значение

(3.37а)

Подставив в эти выражения 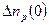и 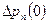из (3.34), получим

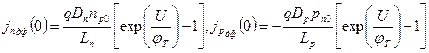(3.38)

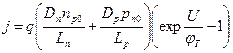
По закону непрерывности тока найденная плотность будет в любом сечении n- и р-областей. Умножив на площадь сечения перехода S, получим формулу для тока:

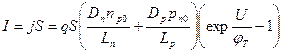(3.39)

Окончательно запишем эту формулу в виде

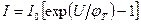(3.40)

где

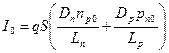(3.41)

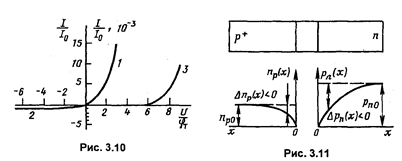
Выражение (3.40) и представляет собой вольт-амперную характери­стику идеализированного р-n-перехода (формула Шокли), а пара­метр 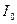называется тепловым током, так как его значение сильно зависит от температуры. Расчетные ВАХ приведены на рис. 3.10.

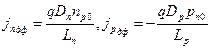
Зависимость 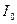(T) характеризуют температурой удвоения DT_удв – приращением температуры, приводящим к удвоению тока 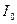. Нетру­дно убедиться, что

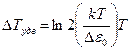(3.42)

При Т = 293К (t = 20°С) для кремния DТ_удв = 5°С, для германия DТ_удв = 8°С, для арсенида галлия DТ_удв = 3,6°С. Нетрудно также определить изменение тока при любом приращении температуры 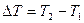: 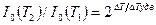. Например, при изменении рабочей темпера­туры от –20 до 60°С отношение составит: для германия 2¹⁰ = 1024, для кремния 2¹⁶ = 6,55·10⁴ и для арсенида галлия 2²² = 4×10⁶.