Концентрация основных и неосновных носителей в примесных полупроводниках

Эти величины, как уже отмечалось, могут быть легко опреде­лены в результате совместного решения уравнений (2.13) и (2.16) или (2.17).

Для n-полупроводника, решив совместно уравнения (2.13) и (2.16), получим

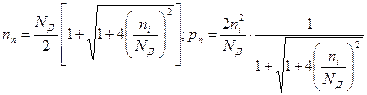(2.18)

В n-полупроводнике концентрация доноров на несколько поряд­ков больше 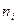( 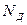>> 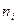), поэтому вместо (2.18) можно записать

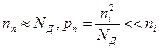(2.19)

В n-полупроводнике электроны являются основными носителя­ми, а дырки неосновными, так как >>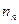

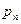
Пример. Концентрация доноров в германии 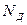= 10¹⁶ см^-3, 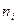= 2,4 10¹³ см ^-3. Концентрация электронов (основных носителей) по формуле (2.19) составит 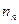= = 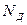10¹⁶ см ^-3, концентрация дырок (неосновных носителей) 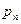= 5,76·10²⁶/10¹⁰= 5,76·10¹⁰ см ^-3.

Аналогично для р-полупроводника из уравнений (2.13) и (2.17) получим

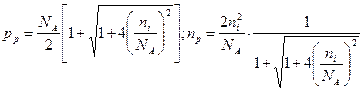(2.20)

При выполнении условия >>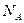

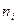
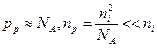(2.21)

где 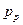- концентрация основных носителей, a 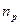- неосновных носи­телей ( >> ).

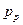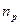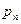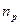Результаты (2.19) и (2.21) следовало ожидать, так как при ра­бочих температурах практически все примесные атомы ионизиро­ваны. Но тогда и концентрации неосновных носителей и мож­но найти из точных формул (2.18) и (2.20), подставив в них 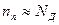и 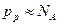, т.е.

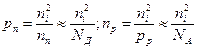(2.22)

На основании формул (2.22) можно сделать важный вывод, что концентрация неосновных носителей очень сильно зависит от ве­щества. Так как для Si 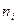= 1,45·10¹⁰ см ^-3, а для Ge 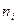= 2,4·10¹³ см ^-3, то концентрация неосновных носителей, пропорциональная 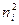, у Ge будет в (2,4·10¹³/1,45·10¹⁰)² 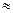3·10⁶ раз выше, чем у кремния. Это объясняется различием в ширине запрещенной зоны. Кроме того, концентрации неосновных носителей сильно зависят от температуры, так как от нее по формуле (2.12) экспоненциально зависит .

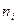При некоторой температуре концентрация 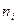, сравнивается с концентрацией доноров 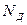в n-полупроводнике. Назовем эту тем­пературу максимальной (T_mах). При Т>T_mах 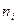> 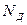, т.е. концентра­ция электронов будет определять­ся не примесью, и поэтому теряет смысл термин «основные носители». В результате генерации пар носителей концентрации электро­нов и дырок оказываются одинако­выми, как в собственном полупро­воднике, и с ростом температуры увеличиваются по экспоненциальному закону. Аналогичный процесс происходит при росте темпера­туры в р-полупроводнике.

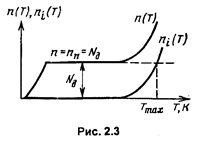
На рис. 2.3 показана температурная зависимость концентрации электронов в кремнии n-типа. Существует подъем кривой на началь­ном участке от T=0 К до некоторой температуры, при которой закон­чится ионизация доноров. Затем в довольно широком диапазоне температур (включающем комнатную) концентрация равна концент­рации примеси, т.е. электроны являются основными носителями. При высоких температурах (Т > T_mах) концентрация определяется генерацией пар носителей, т.е. величиной 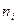, экспоненциально рас­тущей с повышением температуры.

2.1.5. Положение уровня Ферми в полупроводниках

В собственном полупро­воднике n = р = 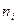, поэтому энергия уровня Ферми в нем из

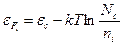(2.23)

Подставляя в (2.23) 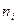из (2.12) и учитывая, что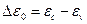

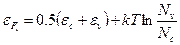(2.24)

Таким образом, в собственном полупроводнике уровень Ферми практически на­ходится в середине запрещенной зоны.

Уровень Ферми 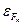в n-полупроводнике определяется при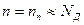

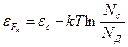(2.26)

Умножая числитель и знаменатель второго слагаемого на 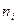и используя форму­лу (2.23), получаем

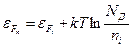(2.27)

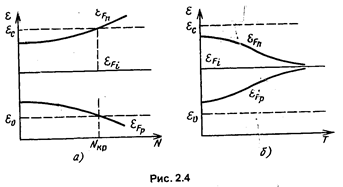
Значения концентрации приме­си, при которой положение уровня совпадает с границей зон, называют критическим ( ).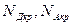

2.1.6. Распределение носителей заряда по энергии

Перемножив значения 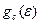и f(ε), получим распределение носителей по энергии в зоне про­водимости (рис. 2.5,в). Что каса­ется валентной зоны, то в соот­ветствии с выражением (2.2) 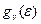надо умножать на [1 –f(ε)]. Все распределения имеют максимум, а затем быстро спадают.