Фазовые переходы в растворах

1. Давление насыщенных паров над раствором. Если в жидкости растворить нелетучее вещество, то на поверхности в верхнем слое раствора часть молекул жидкости будет заменена нелетучими молекулами растворенного вещества. В результате площадь поверхностной пленки, через которую могут диффундировать в пар молекулы жидкости, уменьшается. Поэтому уменьшается и поток диффузии молекул жидкости в пар. Для уравновешивания этого уменьшенного потока требуется уже пониженное давление паров.

Количественную зависимость между давлением пара и концентрацией раствора открыл в 80-е годы 19 в. Франсуа Рауль: 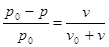. Закон Рауля (27.1)

Относительное понижение давления насыщенного пара растворителя над поверхностью слабого раствора нелетучего вещества равно молярной доле растворенного вещества.

Здесь р₀ – давление насыщенного пара над чистым растворителем, р – давление пара над раствором, v – число молей растворенного вещества в единице объема раствора, v₀ – число молей растворителя в единице объема раствора.

Закон Рауля справедлив для идеальных растворов, когда растворенное вещество не является поверхностно-активным. В этом случае относительная концентрация молекул растворенного вещества в верхнем молекулярном слое такая же, как и во всем объеме раствора.

Закон Рауля справедлив и для парциальных давлений паров, когда все компоненты раствора летучи. Здесь требуется лишь одно условие: чтобы пары не взаимодействовали химически между собой.

2. Повышение точки кипения растворов. На рис.112 показана зависимость давления насыщенных паров чистого растворителя от температуры (сплошная линия) и зависимость от температуры давления паров растворителя над раствором (штриховая линия).

Так как давление паров над раствором ниже, чем над чистым растворителем, то в соответствии с законом Рауля понижение штриховой линии равно p₀ - p = p₀nç(n₀ + n).

Пусть при внешнем давлении р₀ чистый растворитель кипит при температуре Т₀. Чтобы закипел раствор, его надо дополнительно нагреть до температуры Т > Т₀, чтобы давление его насыщенных паров достигало р₀. Найдем это повышение температуры Т - Т₀.

Запишем закон Рауля для изотермы Т₀. 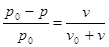. (27.2)

Чтобы определить DT_кип, используем ур-е Клапейрона – Клаузиуса: 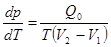. (27.3)

Здесь Q₀ – теплота испарения растворителя. Левая часть уравнения выражает угловой коэффициент касательной в треугольнике ВАС: 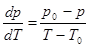. (27.4)

Объемом жидкости V₁ пренебрежем, а объем пара V₂ выразим из уравнения Клапейрона – Менделеева, V₂ = nRT₀çp. Тогда уравнение (27.3) принимает вид:

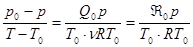. (27.5)

Разделим уравнение (27.2) на (27.5).

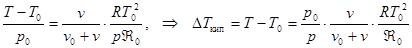. (27.6)

3. Эбулиоскопия (от лат. ebullio - вскипаю) – это метод физико-химического исследования, основанный на измерении повышения температуры кипения растворов.

Применяется в основном для определения молярных масс нелетучих растворяемых веществ.

Упростим формулу (27.6). Поскольку метод лучше применяется к слабым растворам, в которых молекулы растворенного вещества редки и в поверхностном слое не «затеняют» друг друга, то n << n₀. Поэтому слагаемым n в знаменателе можно пренебречь.

Давление р₀ и р в слабых растворах мало отличаются друг от друга, их отношение близко к 1. Например, в 1%-м водном растворе поваренной соли р₀ ç р = 1,003. Поэтому можно принять, что р₀ ç р = 1. 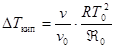. (27.7)

Перейдем от концентрации в молярной доле к весовой концентрации. Так как n = mçM, n₀ = m₀çM₀ где М и М₀ – молярные массы растворенного вещества и растворителя, то 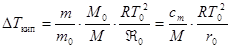. (27.8)

Здесь с_m = mçm₀ - весовая концентрация растворенного вещества, r₀ = Â₀çM₀ - удельная теплота испарения растворителя.

Разрешив выражение (27.8) относительно М, получаем формулу для определения молярной массы растворенного вещества. 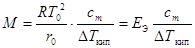. (27.9)

Коэффициент RT₀²çr₀ = E_э называется эбулиоскопической константой. Он зависит только от свойств растворителя.

4. Понижение температуры затвердевания растворов из-за уменьшения давления насыщенных паров над раствором не столь очевидно, как повышение температуры кипения растворов. Однако опыт показывает, что температура замерзания растворов понижается и тем сильнее, чем больше концентрация раствора.

Найдем зависимость DT_затв от концентрации. Для этого рассмотрим участок диаграммы равновесия в окрестности тройной точки. На рис.113 показана опытная диаграмма равновесия воды. Поскольку величина DT_затв того же порядка, как и DT_кип и сравнительно невелика, то масштаб рисунка укрупнен. Интервал температур по горизонтальной оси не превышает 16 градусов.

Хотя на рисунке это проявляется слабо, кривая конденсации ОА идет положе, чем кривая возгонки ОС. Поэтому кривая конденсации раствора О'А' (штриховая линия) пересекает кривую возгонки ОС в точке О'.

Температура плавления воды Т_пл отличается от ее тройной точки Т_тр на одну сотую градуса. Поэтому в данной задаче вполне корректно считать, что температурное смещение тройной точки раствора соответствует смещению точки плавления.

Запишем уравнение Клапейрона – Клаузиуса для перехода твердое тело – пар (кривая возгонки ОС) и для перехода жидкость – пар (кривая испарения ОА) для чистого растворителя. 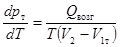, 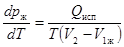. (27.10)

Здесь р_т – давление равновесного пара над твердым телом, р_ж – давление пара над жидкостью, Q_возг - теплота возгонки, Q_исп – теплота испарения.

Пренебрежем объемами твердого тела V_1т и жидкости V_1ж, а объем пара выразим из уравнения Клапейрона – Менделеева, V₂ = nRTçp. Тогда Q_исп çn = Â, Q_возг çn = D и

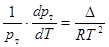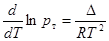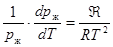, или , , или 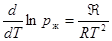. (27.11)

Вычтем 2-е уравнение из 1-го. 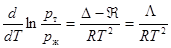. (27.12)

Здесь, L = D - Â - молярная теплота плавления. Это уравнение описывает процесс плавления – затвердевания чистого растворителя. Однако его можно приспособить и к растворам.

При температуре затвердевания раствора р_т есть парциальное давление над раствором, то есть р_т = р. Величина р_ж = р₀ есть давление паров над чистым растворителем. Тогда 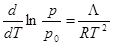. Из закона Рауля 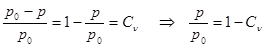. (27.13)

Подставляем: 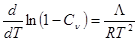. (27.14)

Для интегрирования уравнения надо знать L(T). В столь малом температурном диапазоне, о котором идет здесь речь, можно полагать L = const. У воды, например, в диапазоне температур Т_тр ± 10 К DLçL< ±1%.

Интегрируем 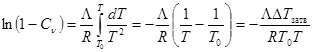. (27.15)

Здесь Т₀ и Т – температуры замерзания соотв-но чистого растворителя и раствора, , DT_затв = Т₀ - Т. Так как Т₀Т 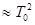, ln(1 - С_n) = - С_n при С_n <<1, то 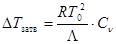. (27.16)

5. Криоскопия (от греч. kryos – холод) – это метод физико-химического исследования, основанный на измерении понижения температуры замерзания растворов по сравнению с температурой замерзания чистого растворителя. Используется обычно для определения молекулярной массы растворенного вещества.

Перейдем от концентрации в молярной доле к массовой. Поскольку 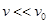, пренебрежем 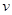в знаменателе. 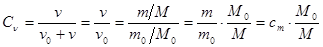. (27.17)

Подставляем в формулу (27.16). Приняв во внимание, что LçM₀ = l - удельная теплота плавления растворителя получаем: 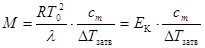. (27.18)

Здесь 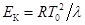- криоскопическая постоянная растворителя.

Метод криоскопии точнее метода эбулиоскопии и потому используется чаще. Его разработал и ввел в практику Франсуа Рауль в 1885г.

6. Кипение жидких смесей. Рассмотрим смеси из двух жидкостей (бинарные системы), растворяющихся друг в друге неограниченно. Такие системы образуют не только близкие по химическим свойствам органические вещества (бензол – толуол, метиловый и этиловый спирты), но и простые неорганические вещества (азот – кислород).

Свойства таких систем описывают с помощью диаграмм состояния, которые могут строится как при постоянном давлении, так и при постоянной температуре.

Ограничимся диаграммами состояния при р = const. Чтобы построить диаграмму для одной бинарной системы жидкостей А + К (азот + кислород) нужно выполнить серию опытов по кипячению смесей с разным соотношением компонентов при p = const. Для этого используется установка, показанная на рис.114. В цилиндр с подвижным поршнем, поставленный на нагреватель, наливают некоторое количество смеси, содержащей, допустим, 90% жидкости А и 10% жидкости К (рис.114-а).

При нагревании температура смеси растет и при каком-то ее значении Т₁ жидкость закипает. В отличие от чистых жидкостей, кипящих при постоянной температуре, смеси кипят в интервале температур от Т₁ до Т₂. Поэтому для продолжения кипения температура должна повышаться. Если некоторая температура Т в интервале от Т₁ до Т₂ останется постоянной, то после испарения части жидкости испарение прекратиться. Между жидкостью и паром установится равновесие (рис.114-б). Если температуру повышать, то кипение будет продолжаться вплоть до некоторой температуры Т₂, при которой вся жидкость выкипит (рис.114-в).

При понижении температуры процесс пойдет в обратном направлении. При температуре Т₂ начнется конденсация, при температуре Т₁ она закончится. Система вернется в исходное состояние.

Проведя такие опыты со смесями разных соотношений, уменьшая постепенно содержание компонента А и увеличивая содержание компонента К, можно получить пары значений Т₁ и Т₂, множества которых в системе координат температура Т – концентрация С образуют кривые – диаграмму состояния.

На рис.115 показана диаграмма состояния бинарной системы азот – кислород при атмосферном давлении. По вертикальной оси откладывается температура, по горизонтальной – весовая концентрация по одной из компонент, здесь – кислорода, растущая слева направо. Для наглядности на вспомогательной оси отложена концентрация азота, растущая справа налево. Их сумма в любой точке оси равна 100%.

Температура 77 К в точке А левого конца диаграммы есть точка кипения чистого азота, а температура 90 К в точке К правого конца есть точка кипения чистого кислорода. Верхняя линия называется кривой пара, нижняя – кривой жидкости. В зависимости от температуры кипения диаграмма позволяет судить о составе жидкой смеси и пара.

Пусть смесь нагревается в открытом пространстве – на воздухе или в сосуде, из которого пар удаляется. Допустим, мы взяли смесь с 70% кислорода и 30% азота. При нагревании смеси температура растет до пересечения вертикальной линии с кривой жидкости в точке Ж. Этой точке соответствует температура Т₁ = 84 К, при которой смесь закипает.

С повышением температуры при кипячении смеси в открытом пространстве состав жидкой смеси меняется, поскольку быстрее выкипает легкокипящая жидкость. При температуре Т = 86 К горизонталь этой температуры пересекает кривую жидкости в точке И. Это значит, что при Т = 86 К в жидкой смеси содержится уже 80% О₂ и 20% N₂ (см. на ось концентраций).

При дальнейшем повышении температуры точка И будет двигаться по кривой в точку К. Остатки смеси в точке К будут содержать практически один кислород. Если начальная температура кипения зависит от концентрации исходной смеси, то конечная температура кипения в открытом пространстве всегда соответствует температуре точки К. На этом явлении основана ректификация – метод разделения смесей жидкостей.

Существуют бинарные системы, у которых точка максимума или минимума находятся не на краях диаграммы, а где-то между ними. Состав раствора при выкипании таких смесей стремится не к чистому компоненту, а к раствору определенной концентрации, кипящему и испаряющемуся далее как химически однородное вещество. Такие нераздельно кипящие смеси называются азеотропными (от греч. a – не, zeo – киплю, trope – изменение). Существование азеотропных смесей открыл в 1810г. Дж. Дальтон.

Одни азеотропные смеси кипят при более высокой температуре, чем их чистые компоненты, другие при более низкой. Например, азеотропная смесь из 95,6% этилового спирта (t_кип = 78,5°С) и 4,4% воды (t_кип = 100°С) кипит при температуре 78,15°С. Получить спирт более высокой концентрации методом перегонки невозможно.