Испарение и конденсация

8. Испарение – переход вещества из жидкого состояния в газообразное. При испарении поглощается энергия, т.к. каждая молекула, переходящая из жидкости сквозь поверхностный слой в газ, совершает работу по преодолению сил межмолекулярного притяжения.

В газ переходят лишь те молекулы, энергия которых больше работы перехода. Поэтому средняя энергия оставшихся в жидкости молекул уменьшается, испаряющаяся жидкость охлаждается. Для поддержания интенсивности испарения постоянной к жидкости нужно подводить тепло. Одновременно с испарением происходит конденсация, то есть переход молекул из пара в жидкость. Если преобладает испарение, то количество жидкости уменьшается, а пара - увеличивается. Если преобладает конденсация, ситуация противоположная.

Между потоками молекул может быть и равновесие. Оно наступает при определенной для данной температуры плотности пара. Эту плотность называют равновесной, а пар насыщенным. Состояние равновесия является динамическим. Давление насыщенного пара называют часто упругостью насыщенного пара.

9. Теплота испарения – это энергия, необходимая для испарения жидкости без изменения температуры при внешнем давлении, равном давлению насыщенных паров при этой температуре. Различают ещё молярную и удельную теплоту испарения. Молярная Â=Qçn – это теплота, необходимая для испарения 1 моля жидкости. Единица измерения Â – Джçмоль. Удельная теплота испарения – это теплота r, необходимая для испарения 1 кг жидкости. Единица измерения r – Джçкг. Очевидно, r = Qçm=ÂçM, где М – молярная масса жидкости.

В таблице 26 приведены значения молярной Â и удельной r теплоты испарения некоторых веществ при температуре их кипения при нормальным давлении p =1,01×10⁵ Па.

Таблица 26

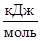
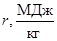
Вещество	Ткип, К	Â,			Вещество	Ткип, К	Â,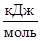
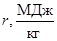
Азот	77,4	5,58	0,199		Кислород		6,82	0,213
Ацетон		30,2	0,521		Углекислота СО2		12,0	0,573
Вода		40,6	2,256		Ртуть		58,6	0,293
Водород		0,908	0,454		Спирт этил.		41,7	0,906
Воздух	81-78	5,71	0,197		Эфир этил.		26,3	0,355

Теплота испарения складывается из двух частей, Q = Q_p + Q_a. Член Q_p есть работа, совершаемая паром по преодолению внешнего давления, Q_p= p(V₂– V₁). (24.1)

Здесь V₁ – объем жидкости, V₂ – объем пара. Член Q_a определяет работу выхода молекул через поверхностный слой.

Например, для 1 моля воды при 100°С Q = Q_p + Q_a = (3540 + 37060) Дж = 40600 Дж. Отношение Q_pçQ_a = 3540ç37060 » 0,1 (для воды). При испарении в вакууме Q_p = 0.

10. Зависимость теплоты испарения от температуры. С повышением температуры различие в энергиях молекул жидкости и пара уменьшается. Поэтому теплота испарения с ростом температуры уменьшается и в критической точке, где исчезает различие между жидким и газообразным состояниями, обращается в нуль. Теоретически не удается получить простую зависимость r(T). 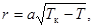Однако она хорошо апроксимируется эмпирической формулой (24.2)

где Т_к – критическая температура жидкости, а – коэффициент, свой у разных жидкостей.

На рис.100 сплошной линией показана опытная зависимость r(T) для воды. Штриховая линия вычислена по формуле (24.2). Коэффициент а определен при Т=373 К и составляет для воды а = 0,136 МДж| (кг×К^1|2).

В пределах от 0 до 100°С формула (24.2) завышает значение r не более чем на 6%. При t > 100°С формула прогнозирует меньшее значение r. Относительная погрешность Dr/r растет по мере приближения к критической температуре, достигая – 11% к 250°С и – 17% к 300°С. Максимального значения - около 50% - относительная погрешность достигает в окрестности критической температуры. Это вполне приемлемое приближение позволяет использовать формулу (24.2) для теоретических оценок.

11. Зависимость давления насыщенных паров от температуры можно найти в явной форме из уравнения Клапейрона – Клаузиуса, если:

а. Пренебречь объемом жидкости по сравнению с объемом пара. Для 1 моля воды, например, V₁ = 0,018 л, а V₂(пар) = 22.4 л. Отношение V₁(вода) ç V₂(пар) = 0,018 ç 22,4 » 0,001. Это вполне приемлемое условие.

б. Допустить, что к пару применимо уравнение Клапейрона – Менделеева. При температурах меньших 100°С давление Н₂О, вычисленное по формуле p = rRTçM, где r - реальная плотность пара, заметно отличается от реального давления лишь вблизи температуры кипения и приближается к +1,5% при 100°С. С дальнейшим ростом температуры погрешность меняет знак и достигает –3% при 200°С. Это также вполне приемлемая точность.

С учетом принятых условий запишем уравнение Клапейрона – Клаузиуса для жидкости и пара: 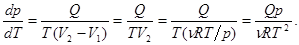(24.3)

Для того, чтобы его проинтегрировать, надо знать зависимость теплоты испарения Q от температуры Т. Если воспользоваться эмпирической формулой (24.2), то после разделения переменных уравнение принимает вид: 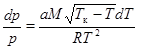. (24.4)

Если перейти к безразмерной переменной x = (T_к-TçT_к, то T_к - T = Т_кх, 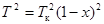, dT = - T_к dx. Уравнение (24.4)принимает вид: 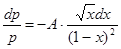. (24.5)

Здесь 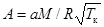- безразмерный коэффициент. Интегрируем правую часть уравнения по частям. Обозначим 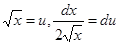. . 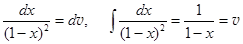(24.6)

Отсюда, 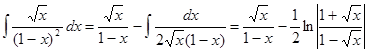. (24.7)

Жидкости существуют при температурах Т < Т_к. Поэтому 0£ x < 1. Выражение под знаком логарифма всегда положительно, поэтому модульные скобки можно опустить. Зависимость давления насыщенных паров от температуры принимает вид:

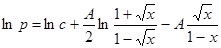, или 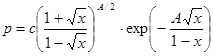. (24.8)

Постоянную интегрирования с лучше определять в той области температур, в которой предполагается использование формулы для расчетов. Для воды, например, А =11,60. Если постоянную с вычислить при температуре 200°С, х₀=(Т_к- Т₀) ç Т_к=(647-473) ç 647 =0,269 и найденное из опыта при температуре Т₀=473 К p₀=15,55×10⁵ Па, то с =7,42 МПа.

Вычисленное при этом значении с давление насыщенных паров при 0°С больше действительного на 6%, а в критической точке меньше его в 3 раза.

На рис.101 сплошной линией показана зависимость давления насыщенных паров воды р_нас от температуры, измеренная в опытах. В интервале температур от 0°С до 100°С давление паров растет от 611 Па до 101 кПа, то есть на три порядка. При критической температуре р_нас=22 МПа.

Штриховой линией показана зависимость р_нас(Т), вычисленная по формуле (24.8).

12. Водяной пар в атмосфере. Влажность. Наличие водяных паров в атмосфере имеет большое значение как для динамики атмосферных процессов, так и для живой природы.

Масса водяных паров в единице объема воздуха называется абсолютной влажностью и обозначается Е. Очевидно Е = r, где r - плотность водяных паров в воздухе.

Максимальная абсолютная влажность Е_mах в обычных условиях соответствует плотности насыщенных паров r_нас при данной температуре. Большую часть времени содержание паров в приземном слое умеренного пояса меньше Е_mах. Отношение плотности паров в воздухе r к плотности насыщенных паров в воздухе при данной температуре называется относительной влажностью е, 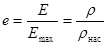. (24.9)

Относительную влажность е определяют также через отношение давлений е = рçр_нас. Поскольку насыщенные пары при высоких температурах не очень хорошо подчиняются уравнению Клапейрона – Менделеева p = rRTçM, рост давления несколько отстает от роста плотности, то относительная влажность е, найденная через отношение давлений, на 1 - 2% больше влажности, вычисленной через отношение плотностей: 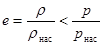. (24.10)

Если при некоторой температуре Т воздух далек от насыщения, относительная влажность меньше 100%, то при охлаждении воздуха относительная влажность е повышается и при некоторой температуре Т_рос может достигнуть 100%.

Рост величины е объясняется тем, что хотя числитель дроби e =rçr_нас пока не меняется, знаменатель r_нас с понижением температуры падает. Температура Т_рос, при которой знаменатель сравняется с числителем, r_нас= r, называется точкой росы. При дальнейшем охлаждении воздуха, начиная с температуры Т_рос, часть паров конденсируется в виде капель росы. Абсолютная влажность Е = r_нас уменьшается, а относительная остается постоянной и равной 100%.

Природное явление выпадения росы наблюдается в теплое время года при плюсовых температурах в ночное время, когда становится прохладно. Для выпадения росы нужно, чтобы относительная влажность е была достаточно высокой. В этом случае температура воздуха при ночном охлаждении может достигнуть точки росы.

13. Кипение – это процесс испарения при той температуре, при которой давление насыщенных паров оказывается равным внешнему давлению.

Когда р_нас < p_внеш, испарение носит спокойный характер, переход молекул из жидкости в пар происходит только на свободной поверхности жидкости.

Когда температура жидкости достигает того значения, при котором р_нас = p_внеш, паровая фаза может возникать уже в любой точке объема жидкости в виде пузырьков. При достаточно интенсивном подведении к жидкости тепла испарение приобретает бурный характер, образование паровой фазы происходит во всем объеме жидкости. Можно сказать, что кипение – это объемное парообразование.

С повышением давления температура кипения повышается. Это видно из рис.102, на котором показана зависимость давления насыщенных паров воды от температуры. В отличие от рис.101 давление р откладывалось на вертикальной оси в логарифмическом масштабе. Благодаря этому стали графически доступными участки с низкими температурами, а также изменилось направление кривизны кривой.

Чем больше внешнее давление, тем большего значения р_нас нужно достичь, тем до более высокой температуры нужно нагреть жидкость. При атмосферном давлении, когда p_нас=1,01×10⁵ Па, t_кип=100°С. Если давление поднять до трех атмосфер, t_кип повышается до 136°С. При давлении 15 атмосфер вода закипает при температуре около 200°С. Если давление увеличить более 226 атмосфер, соответствующих давлению насыщенных паров при критической температуре t_крит=347°С, то процесс кипения происходить не будет, вода будет переходить в газообразное состояние по всему объему без образования границ раздела жидкой и паровой фаз.

Понижая внешнее давление, можно снижать температуру кипения. Так на вершине горы Джомолунгма, где давление атмосферы составляет 0,36×10⁵ Па, вода закипает при температуре около 75°С.

Чтобы началось кипение, жидкость должна иметь центры парообразования. Ими обычно являются микроскопические пузырьки какого-либо газа. Если центров парообразования нет, жидкость может нагреваться до температуры выше точки кипения. Это метастабильное состояние перегретой жидкости.