Круговые процессы (циклы). КПД цикла Карно

1. Циклы.Круговым процессом (циклом) называется такой процесс, при котором термодинамическая система (тело) после ряда изменений возвращается в исходное состояние. На графике цикл изображается замкнутой линией (рис.10).

После совершения цикла всякая функция состояния, например, внутренняя энергия U, принимает прежнее значение. Следовательно, ее изменение за цикл равно нулю, DU = 0.

Работа, совершаемая термодинамической системой, есть функции процесса, при переходе 1®2 газ расширяется, работа, совершаемая системой, положительна, A_1®2 > 0. Графически эта работа изображается площадью фигуры под кривой перехода 1®2.

При переходе 2®1 газ сжимается под действием внешних сил. Работа отрицательна, A_2®1 < 0. Графически она изображается площадью фигуры под кривой перехода 2®1.

Суммарная работа, совершаемая газом в цикле, в котором система возвращается в исходное состояние другим путем, не равна нулю. Графически она определяется площадью фигуры между кривыми перехода 1®2 и 2®1. A = A_1®2 +A_2®1.

Если цикл протекает по часовой стрелке, работа цикла положительна. Такой цикл называют прямым. Газ в прямом цикле преобразует часть подводимой к нему извне теплоты в механическую работу (рис.11).

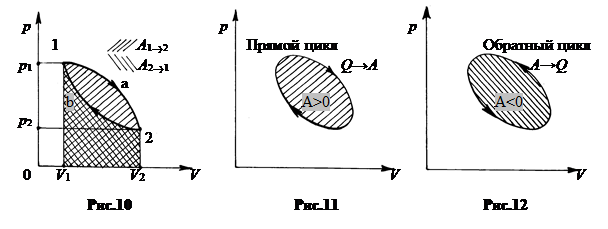
Если цикл совершается против часовой стрелки, работа цикла отрицательна. Газ в обратном цикле преобразует совершаемую над ним работу внешних тел в теплоту (рис.12).

2. Цикл Карно. Прямой цикл может использоваться для превращения теплоты в работу. Он открывает путь к созданию тепловых машин.

Для реализации цикла нужны 3 тела: нагреватель – более нагретое тело, холодильник – менее нагретое тело, рабочее тело – в нашем случае – идеальный газ. Форма циклов может быть какой угодно, лишь бы они были замкнуты.

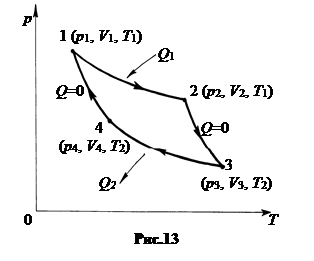В 1824 г. Сади Карно предложил цикл, составленный из двух изотерм и двух адиабат. Исследование этого цикла позволило выявить в нем замечательные свойства и использовать его позднее как метод изучения термодинамических систем.

Пусть рабочим телом являются n молей идеального газа, исходное состояние 1 которого имеет параметры p₁, V₁, T₁ (рис.13).

Теплоемкость нагревателя и холодильника полагаем настолько большой, что их температуры при теплообмене с рабочим телом не меняются. Такие тела называют еще термостатами. Температура холодильника T₂ < T₁. Рассмотрим процессы цикла.

а. Изотермическое расширение 1®2, T₁ = const. В исходном состоянии 1 рабочее тело (идеальный газ) имеет тепловой контакт с нагревателем. Газ расширяется при T₁ = const, давление падает по изотерме от p₁ до p₂. Подводимая к газу теплота полностью превращается в работу, так как изменение внутренней энергии DU_1®2 = 0. 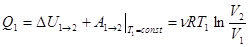. (4.1)

б. Адиабатное расширение 2®3, Q_2®3 = 0. Рабочее тело теплоизолируется и расширяется от объема V₂ до объема V₃ так, что его температура падает от температуры нагревателя T₁ до температуры холодильника T₂. Работа расширения газа совершается за счет его внутренней энергии. . (4.2)

в. Изотермическое сжатие 3®4, T₂ = const. Газ сжимается внешними телами при температуре холодильника T₂ от объема V₃ до V₄. Работа сжатия выделяется в виде теплоты Q₂ и через тепловой контакт отдается холодильнику. Изменение внутренней энергии DU_3®4 = 0.

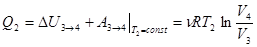. (4.3)

г. Адиабатное сжатие 4®1, Q_4®1 = 0. Газ теплоизолируется и адиабатно сжимается внешними телами до параметров начального состояния p₁, V₁, T₁. Работа адиабатного сжатия на последнем этапе 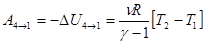. (4.4)

3. Суммарная работа циклаA = A_1®2 + A_2®3 + A_3®4 + A_4®1 = A_1®2 + A_3®4 (4.5)

определяется лишь изотермическими процессами. В адиабатических процессах работа одинакова по величине, но противоположна по знаку. Поэтому ее сумма равна нулю.

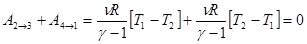. (4.6)

Итак, 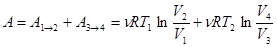. (4.7)

Так как 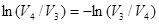, то 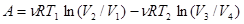. (4.8)

4. КПД цикла Карно. Полная работа цикла равна алгебраической сумме работ, совершаемых рабочим телом в изотермических процессах. При изотермическом расширении газа работа равна полученной от нагревателя теплоте Q₁ = A_1®2 = nRT₁ ln(V₂| V₁).

При изотермическом сжатии часть этой теплоты в количестве Q₂ = A_3®4 = nRT₂ ln(V₃| V₄) отдается холодильнику. Следовательно, при полном цикле в работу превращается не вся теплота Q₁, полученная от нагревателя, а лишь часть ее Q₁ - Q₂.

Эффективность функционирования любой тепловой машины определяется коэффициентом полезного действия h, равным отношению работы A к количеству полученной от нагревателя теплоты Q₁. 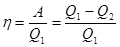. (4.9)

Коэффициент полезного действия идеального цикла Карно

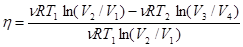. (4.10)

Это выражение можно упростить. Запишем уравнения левой и правой адиабат (по рис.13) в параметрах T и V.

Левая, T₁V₁^g-1 = T₂V₄^g-1, (4.11)

Правая, T₁V₂^g-1 = T₂V₃^g-1. (4.12)

Разделив 2-е уравнение на 1-е получаем: .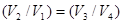

Логарифмы в (4.10) сокращаются, и получаем:

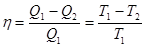. (4.13)

Полученная формула выражает первую теорему Карно: коэффициент полезного действия тепловой машины, работающей по идеальному циклу Карно, зависит только от температур Т₁ и T₂ нагревателя и холодильника, но не зависит от устройства машины и вида используемого рабочего вещества.

Из теоремы Карно следует, что без перепада температур нельзя теплоту превратить в работу.

КПД идеального цикла Карно является наибольшим из всех реальных и мыслимых процессов. Этот факт составляет содержание 2-й теоремы Карно: коэффициент полезного действия всякой тепловой машины не может превосходить коэффициента полезного действия идеальной машины, работающей по циклу Карно с теми же самыми температурами T₁ и T₂ нагревателя и холодильника.

5. Термодинамическая шкала температур. В 1848 г. Уильям Томсон (Кельвин) предложил построить такую температурную шкалу, которая бы не зависела от термометрических свойств реальных тел. Суть его идеи в том, что процесс измерения температуры T₁ некоторого тела реализуется путем проведения цикла Карно между этим телом и некоторым другим телом, температура которого T₀ принимается эталонной. Тогда, как следует из формулы (4.13), количество тепла Q₁, полученного от исследуемого тела, пропорционально температуре T₁.

Для построения шкалы нужно выбрать эталонную (опорную) температуру и приписать ей определенное численное значение.

В 1954 г. 10-я Генеральная конференция по мерам и весам утвердила в качестве опорной температуру тройной точки воды и приписала ей значение 273,16 К точно.

Температуры плавления льда и кипения воды при нормальном атмосферном давлении составляют 273,15 К и 373,15 К приближенно.

Понятия “шкала Кельвина” и “абсолютная термодинамическая шкала температур” в сегодняшнем понимании идентичны.

Конечно, цикл Карно позволяет построить температурную шкалу лишь в принципе. Для практических измерений температуры он не пригоден. На практике эмпирическая температура измеряется всегда с помощью каких-либо реальных термометров. Задача сводится лишь к определению поправок к показаниям таких термометров.

Лучшим приближением к термодинамической шкале являются идеальные газовые термометры, для которых поправок не требуется. Но и идеальных газов в природе нет. Поэтому для практических целей используются реальные газы, приближающиеся по своим свойствам к идеальным. Наиболее подходит для этих целей гелий.