Термодинамическая модель идеального газа. Теплоемкость

Основные понятия. Первый закон термодинамики

1. Предмет термодинамики. Термодинамика – это раздел физики, изучающий явления, в которых наряду с механическим движением макротел происходит изменение их температуры. Основу термодинамики составляет учение о связи и взаимопревращениях разных видов энергии, теплоты и работы.

Теплота не есть особая форма энергии. Это мера переданной телу или отданной им энергии хаотического молекулярного движения.

Работа – это мера переданной от одного тела другому механической энергии тел.

2. Термодинамической системой называется одно или несколько тел, образующих систему, которая подвергается какому-либо энергетическому воздействию: нагреванию, сжатию, освещению и др. Признаки, определяющие состояние системы, называются термодинамическими параметрами. Обычно это давление p, объем V и температура T.

Всякое изменение параметров системы называется термодинамическим процессом. Если система так взаимодействует с внешними телами, что ее параметры не изменяются во времени, то говорят, что система находится в термодинамическом равновесии с окружающей средой.

3. Термодинамические параметры.

а. Давление p, как и в механике, определяется отношением силы dF, действующей нормально на площадку dS, к величине этой площадки, p = dF|dS. Единица p в СИ – паскаль (Па). 1 Па = 1 Н/м². Часто используется внесистемная единица атмосфера (атм), 1 атм = 1,01×10⁵ Па.

Приборы для измерения давления в газах и жидкостях называют манометрами. Большинство манометров заводского изготовления представляют собой металлическую коробку, объем и форма которой меняются в зависимости от давления. Заводские манометры имеют стрелочный указатель и проградуированную шкалу.

В лабораторной практике часто применяют жидкостные манометры. Они представляют собой U-образную трубку, в которую налита жидкость. При изменении давления в одном из колен высота уровней жидкости меняется. Разностное давление вычисляется по формуле p = rgh, где r – плотность жидкости, g = 9,82 м/с², h – разность высот жидкости в коленах, выраженная в метрах.

б. Объем V характеризует пространственную протяженность системы. В СИ измеряется в кубических метрах (м³). Часто используются кратные единицы литр (л), 1 л = 10^-3 м³, миллилитр (мл), 1 мл = 1 см³ = 10^-6 м³.

в. Температура T характеризует степень нагретости тела. Все температурные шкалы построены так, что рост температурысоответствует направлению изменений в последовательности холодно-тепло-горячо. Наиболее употребительны сейчас шкалы Цельсия, Кельвина и Фаренгейта.

Температурная шкала Андерса Цельсия, 1842 г. Температура по этой шкале обозначается t°C, единица измерения градус. Шкала построена на двух основных опорных точках. Температура в первой опорной точке замерзания воды принята за 0°С, а температура во второй опорной точке кипения воды принята за 100°С. Градус шкалы Цельсия соответствует 1|100 этого температурного интервала. Все температуры, при которых вода существует в жидком или газообразном состоянии, являются положительными. Температуры, при которых вода существует в твердом состоянии, являются отрицательными.

Температурная шкала Уильяма Томсона (Кельвина), 1848 г. Температура по этой шкале обозначается T, единица измерения кельвин (К). Нуль по шкале Кельвина соответствует минимально возможной в природе температуре, при которой прекращается хаотическое движение молекул вещества. Температура по шкале Кельвина всегда положительна, ее называют часто абсолютной температурой, а шкалу Кельвина – абсолютной шкалой температур.

Температурный шаг по шкале Кельвина совпадает с шагом по шкале Цельсия, т.е. 1 К = 1°С. Переход от одной шкалы к другой осуществляется по формуле:

T = 273,15 + t°C. (1.1)

В отличие от практической шкалы Цельсия шкала Кельвина является физической шкалой температур. Температура по шкале Кельвина пропорциональна средней кинетической энергии хаотического движения молекул вещества. Поэтому в фундаментальные уравнения физики входит температура по абсолютной шкале.

Температурная шкала Даниэля Фаренгейта, 1724 г. Она применяется в некоторых странах мира до сих пор. Температура по этой шкале обозначается t°F, единица измерения градус. Шкала построена на четырех основных опорных точках:

0°F – самая низкая температура зимы 1709 г. в Голландии. В производстве термометров воссоздавалась с помощью смеси: лед + NaCl + NH₄Cl,

32°F – температура плавления льда,

98°F – температура человеческого тела,

212°F – температура кипения воды.

Температурный шаг по шкале Фаренгейта меньше шага по шкале Цельсия. Обе эти шкалы связаны соотношением: 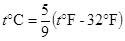. (1.2)

г. Температурная шкала Рене Реомюра, 1730 г. Сейчас она практически вышла из употребления, но широко применялась во Франции и России вплоть до 20 столетия. Опорных точек две: 0°R соответствует точке замерзания воды, а 80°R – точке кипения воды. Шкалы Цельсия и Реомюра связаны формулой: 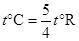. (1.3)

Приборы для измерения температуры называются термометрами. В большинстве термометров в качестве термометрического тела используются жидкости – ртуть или спирт с их термометрическим свойством – способностью при нагревании расширяться.

4. Внутреняя энергия U термодинамической системы тела – фундаментальное понятие термодинамики. В общефизическом смысле величина U есть сумма всех видов энергии, которыми обладает изолированная система, за исключением кинетической и потенциальной энергии системы как целого. То есть сюда входят энергия хаотического движения молекул, энергия взаимодействия молекул, лучистая, ядерная и др.

Но в термодинамике в понятие внутренней энергии включают лишь ту ее часть, которая изменяется в тепловых процессах. То есть в величину U термодинамической системы входят лишь кинетическая энергия хаотического движения молекул и потенциальная энергия их взаимодействия.

Внутренняя энергия U – функция состояния системы. Она определяется значениями термодинамических параметров p, V, T. Изменение внутренней энергии системы при переходе ее из состояния 1 в состояние 2 есть разность между энергиями в этих состояниях, DU = U₂ - U₁. Величина DU не зависит от того, каким путем термодинамическая система перешла из одного состояния в другое.

5. Величины Q и А – функции процесса, в отличие от внутренней энергии U. Сколько тело получит или отдаст теплоты Q и какую оно совершит работу A, зависит от того, каким путем перейдет оно из одного состояния в другое.

При взаимодействии тел обмен энергией между ними может идти двумя путями. Во-первых, путем совершения механической работы А одного тела над другим. Во-вторых, путем передачи от одного тела другому теплоты Q.

Договорились считать, что Q > 0, если система получает теплоту, и Q < 0, когда отдает. Кроме того A > 0, если работу совершает система над внешними телами, и A < 0, если работу совершают внешние тела над системой.

6. Первый закон термодинамики. К середине 19 в. было твердо установлено, что теплота – не вещество, а хаотическое движение микрочастиц тела. В сороковых годах 19 века в работах Юлиуса Майера, Джеймса Джоуля и Германа Гельмгольца было доказано, что закон сохранения энергии выполняется и в тех системах, где действуют диссипативные силы. Для общефизической формулировки этого закона нужно лишь ввести понятие внутренней энергии системы. Обычно первый закон термодинамики записывается так:

dQ = dU + dA. Первый закон термодинамики. (1.4)

Переданное телу количество теплоты dQ идет на увеличение его внутренней энергии dU и на совершение телом работы dA.

Возможны 3 частных случая.

а. Объем тела не меняется. Тогда тело не совершает работы над внешними телами, dA = 0. Закон сохранения принимает вид: dQ = dU. Все подводимое тепло идет на увеличение внутренней энергии тела.

б. Тело в адиабатной оболочке (теплоизолировано), dQ = 0. В этом случае 0 = dU + dA, Þ dA = – dU. Изолированная термодинамическая система может совершать работу только за счет убыли своей внутренней энергии.

в. Тело в изотермическом процессе, его температура постоянна. Но это значит, что постоянна и его внутренняя энергия, dU = 0. Тогда dQ = dA. Вся подводимая к системе теплота идет на совершение работы.

7. Вечный двигатель 1-го рода. С развитием капитализма в Европе в 17 веке появляется нужда в механизмах, способных совершать механическую работу. В течение длительного времени идеалом такого механизма была воображаемая машина, которая, будучи раз приведенной в движение, продолжала бы неограниченно долго совершать механическую работу, не потребляя энергию извне. Ее назвали вечным двигателем 1-го рода, на латыни – Perpetuum mobile 1. Было предложено множество проектов таких псевдомашин, но все они не оправдали надежд их создателей.

В 17 веке Рене Декарт установил закон сохранения импульса, в начале 18 – Готфрид Лейбниц пришел к идее закона сохранения механической энергии. А в середине 19 века, когда Майер, Джоуль и Гельмгольц обосновали общефизический закон сохранения энергии, стало окончательно ясно, что если тело не получает извне теплоту, то оно может совершать работу только за счет убыли своей внутренней энергии. Поскольку внутренняя энергия тела ограничена, то и работа, которую можно получить за ее счет, тоже ограничена. Поэтому 1-й закон термодинамики (закон сохранения энергии) можно сформулировать еще так: вечный двигатель 1-го рода невозможен.

8. Методологическая роль 1-го закона термодинамики состоит в том, что он является критерием научности исследования. Не нужно тратить умственную энергию на изобретение машин, принцип действия которых противоречит законам природы. Наоборот, выполнимость этого закона является надежным признаком правильности физической модели.

Термодинамическая модель идеального газа. Теплоемкость

1. Законы разреженных газов. Из трех агрегатных состояний, в которых может находиться вещество, самым простым является газообразное. Первым газом, который люди стали воспринимать как особое состояние вещества, был атмосферный воздух. С воздухом проводились первые физические эксперименты, которые привели к открытию первых опытных газовых законов.

PV|_T=const=const. Роберт Бойль, 1662, Эдм Мариотт, 1676(2.1)

V|_p=const=V₀(1 + at). Жозеф Гей-Люссак, 1802 (2.2)

p|_V=const=p₀(1 + bt). Жак Шарль, 1787 (2.3)

Здесь a и b - коэффициенты пропорциональности, V₀ и p₀ – объем и давление газа при t = 0°C.

Позднее, когда удалось получить “чистые” газы кислород O₂, азот N₂ и более сложные CO₂, CH₄ и так далее, выяснилось, что этим законам подчиняются практически все газы при низких давлениях (менее 1 атмосферы). Поэтому перечисленные законы называют законами разреженных газов. В 1834 г. Бенуа Клапейрон объединил эти три эмпирических закона в одно уравнение. 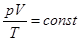. Бенуа Клапейрон, 1834 (2.4)

Позднее выяснилось, что значение константы пропорционально массе газа m и обратно пропорционально его молярной массе M. В 1874 г. Дмитрий Менделеев предложил представлять константу в виде произведения R×m/M, где R – постоянный для всех газов коэффициент, его называют универсальной газовой постоянной, R = 8,31 Дж/Моль×К. Отношение m/М = n называют количеством вещества, его измеряют в молях.

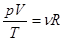, или pV = nRT. Уравнение Клапейрона-Менделеева (2.5)

2. Идеальный газ. С увеличением давления и с понижением температуры уравнение Клапейрона-Менделеева все хуже описывает свойства реальных газов. Поэтому тот воображаемый газ, который удовлетворяет уравнению Клапейрона-Менделеева на всем множестве положительных значений параметров p, V и T, договорились называть идеальным газом, а уравнение Клапейрона-Менделеева – уравнением состояния идеального газа.

Здесь не строится никаких гипотез относительно внутренней структуры идеального газа. Он рассматривается как термодинамическая система с известным количеством вещества n в ней и обладающая такими свойствами, которые в макропараметрах p, V и T описываются уравнением (2.5).

3. Уравнение состояния смеси идеальных газов. Идеальные газы не взаимодействуют друг с другом. Поэтому если в сосуде имеется смесь идеальных газов, то каждый из них ведет себя так, как будто других газов в сосуде нет. Каждый идеальный газ занимает весь объем сосуда. Поэтому для каждого из газов можно записать уравнение состояния.

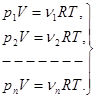(2.6)

Все газы в смеси находятся в термодинамическом равновесии, поэтому их температура T одна и та же.

Давления p₁, p₂, …, p_i,…, p_n создаваемые каждым газом в отдельности, называются парциальными (от лат. рars - часть).

Просуммировав уравнения получаем:

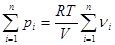. Уравнение состояния смеси идеальных газов (2.7)

В 1801 г. Джон Дальтон эмпирически установил, что сумма парциальных давлений газов равняется давлению смеси идеальных газов, измеряемому манометром.

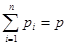. Закон Дальтона парциальных давлений смеси газов (2.8)

4. Изопроцессы (от греч. isos – равный, одинаковый) – это процессы, протекающие при постоянстве какого-либо параметра. В уравнение состояния входят три параметра p, V и T. Поэтому можно выделить 3 изопроцесса.

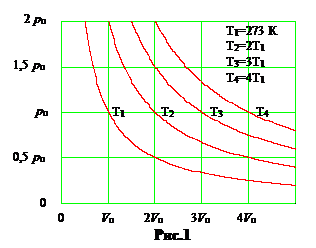а. Изотермический, T = const. Процесс совершается при постоянной температуре. Уравнение состояния упрощается и переходит в закон Бойля-Мариотта, pV = nRT = const.

Кривые, иллюстрирующие изотермический процесс, называют изотермами. В системе координат p, V изотермы представляют собой гиперболы вида p = const/V. Чем выше температура газа T, тем выше на графике соответствующая ей изотерма (рис.1).

Способность газа изменять свой объем V с изменением давления p при постоянной температуре T характеризуется изотермическим коэффициентом сжимаемости c. Все коэффициенты относятся к единичному объему, поэтому 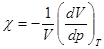. (2.9)

Знак ”T ” в формуле, используемый как индекс, означает постоянство этого параметра при вычислении производной.

Для идеального газа V = const| p. Отсюда 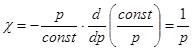. (2.10)

Сжимаемость идеального газа обратно пропорциональна давлению, под которым он находится. Знак “минус” показывает, что увеличение давления приводит к уменьшению объема и наоборот.

б. Изобарический, p = const. Процесс совершается при постоянном давлении. Уравнение состояния переходит в закон Гей-Люссака, V| T = nR/p = const, или V = const×T.

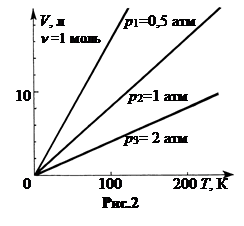
Графики изобарических процессов называют изобарами. В системе координат V и T изобары – прямые линии, проходящие через начало координат. Чем выше давление, тем ниже соответствующая прямая (рис.2).

Способность газа изменять свой объем с изменением температуры при постоянном давлении характеризуется коэффициентом теплового расширения a.

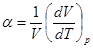. (2.11)

Для идеального газа V = const×T. Отсюда 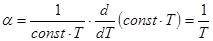. (2.12)

Обычно коэффициент теплового расширения выражается в точке плавления льда, где T = 273,15 K. Тогда a = 1/273,15 K = 3,66×10^-3 K^-1 для всех идеальных газов.

в. Изохорический (от греч. isos и chora – занимаемое место), V = const. Процесс совершается при постоянном объеме. Уравнение состояния переходит в закон Шарля, p/T = nR/V = const, или p = const×T.

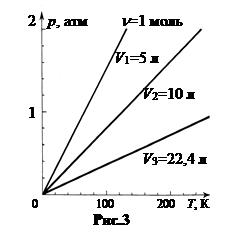
Графики изохорических процессов называют изохорами. В системе координат p, V изохоры – прямые линии, проходящие через начало координат. Чем больше объем, занимаемый газом, тем ниже соответствующая изохора (рис.3).

Способность газа изменять свое давление с изменением температуры при постоянном объеме характеризуется термическим коэффициентом давления 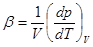. (2.13)

В идеальных газах 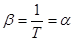. (2.14)

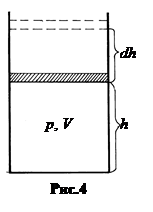
5. Работа идеального газа при изобарическом расширении. Пусть газ заключен в цилиндре с подвижным поршнем (рис.4). Если газ нагревать, он расширяется. Пусть в процессе расширения газа поршень площадью S переместился на расстояние dh под действием силы F= p×S. Работа перемещения поршня dA = Fdh = p×Sdh = pdV. (2.15)

Работа конечного расширения газа 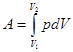. (2.16)

Здесь p есть функция объема V. При p = const A = p(V₂- V₁). (2.17)

С учетом формулы (2.15) первый закон термодинамики: dQ = dU + pdV. (2.18)

6. Теплоемкость идеальных газов. Теплоемкостью тела называют величину C, численно равную количеству тепла, которое нужно подвести к телу или отнять от него для изменения его температуры на 1К. 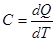. (2.19)

Различают ещё молярную теплоемкость C = С|n и удельную теплоемкость с = С| m, где n и m – количество вещества в теле и его масса. Еденица измерения молярной теплоемкости – Дж| (моль×К), единица измерения удельной теплоемкости – Дж| (кг×К). Если M – молярная масса вещества, между ними такая связь: C = c×M, (2.20)

Поскольку нагревание тел и особенно газов можно проводить как при постоянном объеме, так и при постоянном давлении, то различают изохорную и изобарную теплоемкости. Символы изохорной теплоемкости помечаются буквой V: C_v, C_v , c_v, изобарной – буквой p: C_p, C_p, c_p. Найдем теплоемкости С_v и С_p и связь между ними для идеального газа.

Изохорная теплоемкость газа 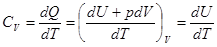. (2.21)

Изобарная теплоемкость газа 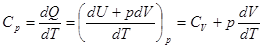. (2.22)

Изохорная теплоемкость тела (системы) определяется лишь изменением его внутренней энергии, C_v = dU| dT. Изобарная больше на величину работы расширения тела. Для вычисления этой работы в случае идеального газа выразим объем газа V из уравнения Клапейрона-Менделеева, V = nRT| p. Продифференцируем по температуре.

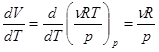. (2.23)

Подставив в (2.22) получаем C_p = C_v+nR. (2.24)

Разделив уравнение на число молей n, получаем связь между молярными теплоемкостями идеального газа. C_p = C_v+R. Юлиус Майер, 1842 (2.25)

Универсальная газовая постоянная R численно равна работе изобарного расширения одного моля идеального газа при нагревании на 1 К.

Измерения, выполненные с одноатомными разреженными газами (Ne, Ar, Kr, пары металлов), показали, что для них C_v = 12,5 Дж/(моль×К) 0@ 3R/2, C _p = 21 Дж/(моль×К) @ 5R/2. Это хорошо согласуется с уравнением Майера. Несколько хуже обстоит дело с двухатомными разреженными газами (O₂, N₂, HCl). Хотя и для них уравнение Майера выполняется с точностью до 2-х знаков. C_v = 21 Дж/(моль×К) @ 5R/2, C _p = 30 Дж/(моль×К) @ 7R/2.

В термодинамике широко применяется величина, равная отношению теплоемкостей

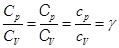(2.26)

и называемая показателем адиабаты. Ее опытное значение составляет с точностью до 2-х знаков для одноатомных газов g = 1,7, для двухатомных газов g = 1,4, для многоатомных газов g = 1,3. Это хорошо согласуется с уравнением Майера.