Тепловые и холодильные машины. Энтропия. Второй закон термодинамики

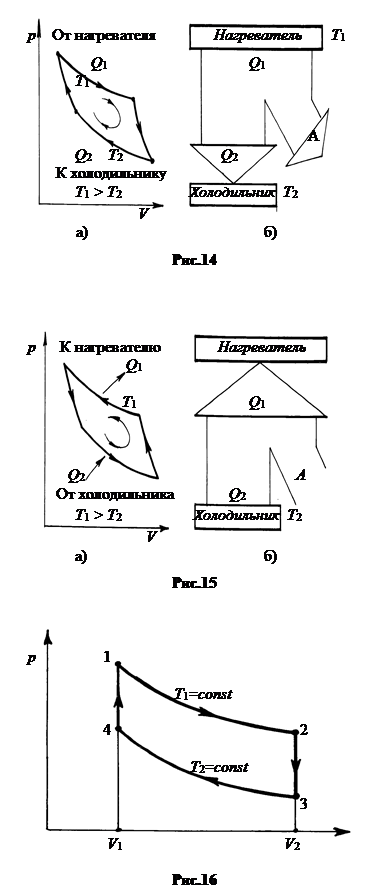1. Тепловая и холодильные машины. Устройство, в котором реализуется круговой цикл, протекающий по часовой стрелке, называется тепловой машиной. Тепловая машина превращает теплоту в работу. Цикл, протекающий по часовой стрелке, называется прямым (рис.14-а). В прямом цикле от нагревателя берется больше теплоты, чем отдается холодильнику Q₁ = Q₂ + A (рис.14-б).

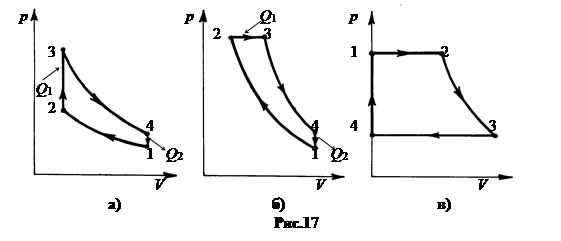
Цикл, протекающий против часовой стрелки, называется обратным (рис.15-а). В обратном цикле теплота берется от холодильника и передается нагревателю (рис.15-б). Для протекания обратного цикла внешние тела должны совершать работу A. В результате нагревателю передается больше тепла, чем взято от холодильника, на величину работы, Q₁ = Q₂ + A. Устройство, в котором реализуется обратный цикл, называется холодильной машиной.

Наряду с циклом Карно в теории тепловых процессов используются и другие циклы. Например цикл Клапейрона, состоящий из двух изотерм и двух изохор (рис.16).

Циклы Карно и Клапейрона называют термодинамическими. Они используются как метод исследования при решении общих термодинамических задач.

В основе работы реальных тепловых машин лежат технические циклы, в которых учитываются тепловые потери. Их идеальные варианты без учета тепловых потерь называются прототипами.

Карбюраторный четырехтактный двигатель внутреннего сгорания работает по циклу, состоящему из двух изохор и двух адиабат (рис.17-а).

Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат, изобары и изохоры (рис.17-б).

Паросиловые установки работают по циклу, состоящему из двух изобар, адиабаты и изохоры (рис.17-в).

а. Карбюраторный двигатель,
Н.Отто, 1876. 1®2 – сжатие рабочего тела (адиабата), 2®3 – сгорание топлива, подвод тепла Q₁ (изохора), 3®4 – рабочий ход (адиабата), 4®1 – отвод тепла Q₂ (изохора).

б. Дизельный двигатель, Р.Дизель, 1892. 1®2 – сжатие рабочего тела (адиабата), 2®3 – сгорание топлива, подвод тепла Q₁ (изобара), 3®4 – рабочий ход (адиабата), 4®1 – отвод тепла Q₂ (изохора).

в. Паросиловая установка, У.Ранкин, 1859. 1®2 – испарение воды при нагревании (изобара), 2®3 – рабочий ход (адиабата), 3®4 – конденсация пара (изобара), 4®1 – перегрев воды Q₂ (изохора).

Холодильные машины также построены на отличных от Карно циклах с использованием фазовых переходов в рабочем теле.

2. Качество энергии. Доказанная самим Карно его вторая теорема утверждает, что из всех мыслимых термодинамических циклов, протекающих при данных предельных температурах T₁ и T₂, цикл Карно имеет самый высокий КПД. Величина (T₁ - T₂)| T₁ определяет верхний предел КПД любой тепловой машины.

Всякая периодически действующая тепловая машина может превратить в работу только часть тепловой энергии. И эта часть тем больше, чем выше температура T₁ нагревателя. Говорят, чем выше температура нагревателя, тем выше качество запасенной в нем энергии.

Всякий самопроизвольно идущий необратимый тепловой процесс приводит к понижению качества энергии.

3. Равенство и неравенство Клаузиуса. Преобразуем выражение КПД идеального цикла Карно.

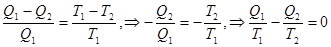. Идеальный цикл (5.1)

По предложению Гендрика Лоренца отношение Q| T называют приведенной теплотой. Следовательно, сумма приведенных теплот, которыми обменивается с окружающими телами рабочее тело, в идеальном цикле равна нулю.

В реальном цикле к теплоте Q₂, отдаваемой холодильнику, добавляется тепло от работы сил трения, поэтому в целом Q₂| T₂ оказывается больше по модулю члена Q₁| T₁. Поэтому сумма приведенных теплот оказывается в целом отрицательной, равенство переходит в неравенство.

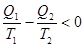. Реальный цикл (5.2)

При обобщении задачи теплоту Q рассматривают как алгебраическую величину, записывая со знаком “плюс”. Кроме того, цикл может состоять из множества, а не только из двух теплообменных процессов. Поэтому обобщенная формула записывается так:

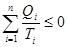. Равенство и неравенство Клаузиуса, 1862 (5.3)

Если в процессах изменяется и температура тепловых резервуаров, то выражение равенства и неравенства Клаузиуса принимает вид интеграла.

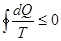. (5.4)

4. Энтропия. Итак, в идеальном цикле нагреватель отдает приведенную теплоту Q₁| T₁, холодильник получает приведенную теплоту Q₂| T₂, а в целом изменение приведенной теплоты в системе тел равно нулю. В 1865 г. Клаузиус установил, что величина Q| T обладает свойствами функции состояния. Эту функцию он назвал энтропией (от греч. entropia – поворот, превращение) и обозначил ее буквой S.

Как и внутренняя энергия U, энтропия S определяется с точностью до постоянной величины. Поэтому обычно речь идет об изменении энтропии.

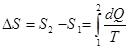. (5.5)

В идеальном цикле энтропия системы нагреватель – рабочее тело – холодильник не меняется. В реальном цикле величина Q₂ увеличивается за счет трения, поэтому энтропия холодильника растет быстрее, чем убывает энтропия нагревателя. Поэтому в целом энтропия системы тел нагреватель – рабочее тело – холодильник в реальном цикле увеличивается.

5. Второй закон термодинамики. Наиболее важным свойством энтропии является ее поведение в реальных процессах, наблюдающихся в природе. Опыт и теория показывают, что в реальных процессах, самопроизвольно протекающих в замкнутых системах, энтропия всегда возрастает.

Рост энтропии в любом процессе продолжается не беспредельно, а лишь до определенного максимального значения, характерного для данной системы. Это максимальное значение энтропии соответствует состоянию равновесия, и после того, как оно достигнуто, какие бы то ни было изменения состояния без внешнего воздействия прекращаются.

Энтропия, как функция состояния, сильно отличается от такой функции состояния, как энергия. Если энергия не может быть ни создана, ни уничтожена, то энтропия может создаваться и она постоянно создается во всяком процессе перехода к равновесию.

Но однажды созданная она уже не может быть уничтожена. Обратный процесс с уменьшением энтропии самопроизвольно идти не может. Этот закон возрастания энтропии при самопроизвольно протекающих процессах, составляет содержание 2-го закона термодинамики: все самопроизвольно протекающие процессы в замкнутых системах развиваются в направлении возрастания энтропии (Р.Клаузиус, 1876).

Если в каком-либо объеме термодинамической системы идет процесс с уменьшением энтропии, то одновременно с ним в других частях системы идет компенсирующий процесс увеличения энтропии так, что полное изменение энтропии в адиабатно изолированной системе положительно. Энтропия возрастает или в крайнем случае не меняется.

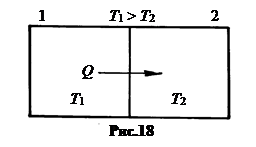В качестве примера найдем изменение энтропии системы из 2-х тел, имеющих разную температуру и находящихся в тепловом контакте (рис.18).

Тело 1 теряет теплоту, dQ₁ < 0, а тело 2 получает эту же теплоту, dQ₂ = –dQ₁ > 0. Полагаем, что теплопередача осуществляется путем обратимых процессов с помощью третьего тела. Это позволяет применить к процессу теплопередачи аппарат термодинамики. Тогда для тела 1 dS₁ = –dQ| T₁, а для тела 2 dS₂ = +dQ| T₂. Общее изменение энтропии в системе есть:

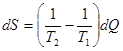. (5.6)

Здесь dQ – положительное число. Выражение в скобках при T₁ > T₂ также положительное число. Следовательно, dS > 0. Энтропия растет. Это значит, что обратный переход тепла от менее нагретого тела к более нагретому должен уменьшать энтропию, а это невозможно. Отсюда вытекает еще одна формулировка 2-го закона термодинамики:

теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому (Р.Клаузиус, 1852).

В 1851 г. Уильям Томсон, анализируя работу тепловой машины, пришел к выводу, что в любом цикле наряду с расширением рабочего тела, в процессе которого совершается работа, обязательно должно быть сжатие. Иначе система не вернется в исходное состояние. Но всякое сжатие сопровождается выделением тепла Q₂, которое передается холодильнику. Следовательно, нельзя полностью превратить в работу теплоту Q₁, взятую из какого-либо теплового резервуара. Это так называемый принцип Томсона. Он является еще одной формулировкой 2-го закона термодинамики:

в природе невозможен процесс, единственным результатом которого была бы механическая работа, совершенная за счет охлаждения теплового резервуара (У.Томсон, 1851).

В конце 19 в. Вильгельм Оствальд предложил назвать эту воображаемую машину, полностью превращающую теплоту в работу, вечным двигателем 2-го рода. Отсюда появляется еще одна формулировка 2-го закона: вечный двигатель второго рода невозможен (В.Оствальд).

6. Тепловая смерть Вселенной. Исходя из 2-го закона термодинамики У.Томсон в 1852 г. и Р.Клаузиус в 1865 г. пришли к выводу, что все процессы во Вселенной закончатся в конце концов термодинамическим равновесием. Все виды энергии перейдут в тепловую, температуры всех тел сравняются. Прекратятся всякие изменения, а значит и жизнь.

В конце 19 в. Людвиг Больцман показал, что этот вывод неверен. Главная ошибка в том, что закон возрастания энтропии при самопроизвольно протекающих процессах применим лишь к замкнутым термодинамическим системам. Тогда как считать Вселенную замкнутой системой нет оснований.

7. Методологическое значение 2-го закона термодинамики. Являясь одним из фундаментальных законов природы, он позволяет не только судить о направлении процессов, протекающих в реальных системах, в которых действуют диссипативные силы, но и построить объективную температурную шкалу, не зависящую от произвола выбора термометрического тела и устройства термометра.

В термодинамике применяются два метода теоретического исследования систем.

а. Метод циклов, который исторически возник первым. Суть его в том, что реальный процесс мысленно заменяется последовательностью искусственно введенных циклов Карно. В настоящем курсе он будет применен для вывода уравнения Клапейрона-Клаузиуса, описывающего фазовые переходы 1-го рода. С развитием термодинамики метод циклов уступил место методу термодинамических функций.

б. Метод термодинамических функций. Его развил к 1902 г. американец Джозайя Гиббс, который ввел 4 функции состояния, позволяющие исчерпывающе полно решить любую задачу термодинамики равновесных процессов. Это внутренняя энергия, энтальпия, свободная энергия Гельмгольца и термодинамический потенциал Гиббса. (Подробнее см. [1], с.с.139-143).