Равновесные процессы
1. Термодинамическое равновесие – это такое состояние термодинамической системы, когда температура T и давление p во всех точках системы одинаковы. При термодинамическом равновесии всякие макроскопические изменения прекращаются.
2. В равновесном процессе система проходит через последовательность равновесных состояний. Равновесным может быть только бесконечно медленный процесс, поэтому он является идеальной моделью медленно протекающих реальных процессов. В настоящем курсе рассматриваются только равновесные процессы.
Равновесными могут быть не только термодинамические, но и механические процессы. Так, при вычислении работы подъема тел в поле силы тяжести в общем случае молчаливо предполагается, что тело поднимается бесконечно медленно, ускорение подъема равно нулю, сила тяги равна по величине силе тяжести mg, поэтому работа подъема A = mgh.
 3. Работа идеального газа в изопроцессах
3. Работа идеального газа в изопроцессах
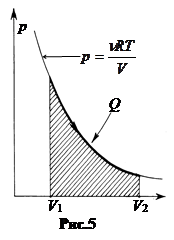
а. Изотермический процесс, T = const. Пусть идеальный газ, взятый в количестве n молей, расширяется от объема V1 до объема V2 при постоянной температуре. Вычислим работу, совершаемую газом. Для этого в формулу dA = pdV подставим p из уравнения Клапейрона-Менделеева и проинтегрируем.
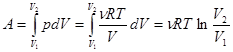 . (3.1)
. (3.1)
Если газ расширяется (рис.5), объем увеличивается, V2 > V1, работа положительна, A > 0. На графике эта работа соответствует площади фигуры в пределах от V1 до V2 под кривой процесса.
 Если газ сжимается (работу совершают внешние тела), V2 < V1, работа отрицательна, A < 0. При расширении к газу должно подводиться тепло, при сжатии – отводиться.
Если газ сжимается (работу совершают внешние тела), V2 < V1, работа отрицательна, A < 0. При расширении к газу должно подводиться тепло, при сжатии – отводиться.
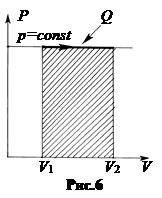
б. Изобарический процесс, p = const. В системе координат p, V графиком изобарического процесса является прямая линия, параллельная оси абсцисс (рис.6). Поскольку давление постоянно, вычисление работы расширения газа упрощается.
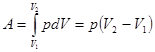 . (3.2)
. (3.2)
Чтобы газ расширялся при постоянном давлении, к нему нужно подводить тепло. Если газ сжимается внешними телами, то для поддержания давления постоянным от газа должно отводиться тепло.
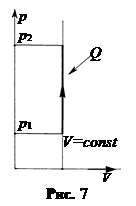 в. Изохорический процесс, V = const. В системе координат p, V графиком изохоры является прямая линия, параллельная оси ординат (рис.7). Объем системы не меняется, работа равна нулю, A = 0. При повышении давления к системе подводится тепло, при понижении – отводится.
в. Изохорический процесс, V = const. В системе координат p, V графиком изохоры является прямая линия, параллельная оси ординат (рис.7). Объем системы не меняется, работа равна нулю, A = 0. При повышении давления к системе подводится тепло, при понижении – отводится.
4. Адиабатный процесс. Наряду с изотермическим, изобарическим, изохорическим процессами, протекающими с теплообменом между системой и окружающей средой, в природе реализуются процессы, протекающие без теплообмена. Обычно это быстрые процессы, когда теплообмен просто не успевает произойти. В этом случае dQ = 0. (Например, распространение звуковых волн). Но можно реализовать и медленный процесс с dQ = 0, если поместить систему в теплоизолирующую оболочку. Такие оболочки называются адиабатными (от греч. a – не, diabatos – проходимый, непроходимая для тепла). Адиабатный процесс также является изопроцессом, поскольку остается неизменной теплоемкость системы, C = dQ| dT = 0 = const.
Найдем уравнение адиабатного процесса для идеального газа. Будем исходить из 1-го закона термодинамики, который здесь принимает вид: 0 = dU + pdV. (3.3)
Так как dU = CV dT, то 0 = dU = CV dT + pdV. (3.4)
В уравнение входит 3 параметра: p, V и T. Сведем это число к двум, выразив T из уравнения Клапейрона-Менделеева. 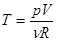 ,
, 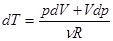 . Подставляем, записав нуль как обычно справа.
. Подставляем, записав нуль как обычно справа. 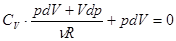 . (3.5)
. (3.5)
Из уравнения Майера nR = Cp- CV. Подставив и избавившись от дробности, получаем:
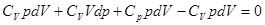 . (3.6)
. (3.6)
Разделив все члены на pVCV и обозначив Cp| CV = g, получаем дифференциальное уравнение адиабатного процесса в переменных p и V: 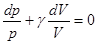 . (3.7)
. (3.7)
Интегрируем. pV g = const. Симеон Пуассон, 1823 (3.8)
Выразив давление p из уравнения Клапейрона-Менделеева получаем уравнение Пуассона в переменных T и V: 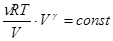 , или TV g-1 = const. (3.9)
, или TV g-1 = const. (3.9)
Если из уравнения Клапейрона-Менделеева выразить объем V, получаем уравнение адиабаты в параметрах p, T: p(nRT/p)g = const, или p1- g×T g = const. (3.10)
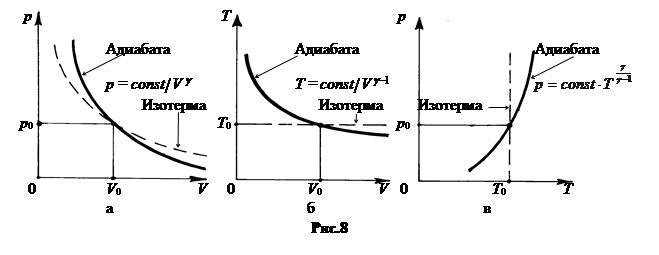 |
На рис.8 показаны графики адиабаты в сравнении с изотермой в координатах p, V (рис.8-а), в координатах T, V (рис.8-б), в координатах p, T (рис.8-в).
5. Работа идеального газа в адиабатном процессе. Вычислим работу в параметрах p, V. Для этого в общее выражение работы (формула (2.16)) подставим p из уравнения Пуассона, p = const| V g. 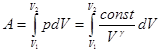 . (3.11)
. (3.11)
После интегрирования получаем: 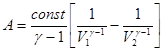 . (3.12)
. (3.12)
Значение константы можно выразить через любое состояние системы. Например, через начальное, p1V1g = const. 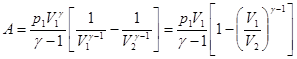 . (3.13)
. (3.13)
Это работа идеального газа в адиабатном процессе в параметрах p, V.
Если записать уравнение адиабаты в параметрах T, V (формула 3.9) для начального и конечного состояний системы, 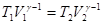 , то (V1| V2)g-1=T2| T1, а p1V1 = nRT1.
, то (V1| V2)g-1=T2| T1, а p1V1 = nRT1.
Подставляем в (3.13). 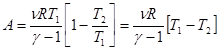 . (3.14)
. (3.14)
Аналогично получим в параметрах p и T. 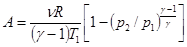 . (3.15)
. (3.15)
6. Уравнение Бернулли для идеального газа. Термодинамическая система может представлять собой не только неподвижный, но и движущийся идеальный газ. В случае медленного движения идеального сжимаемого газа к трем энергиям единичного объема, которые входят в уравнение Д.Бернулли для идеальной несжимаемой жидкости, добавляется еще внутренняя энергия. Поэтому закон сохранения энергии для линии тока идеального газа принимает вид: 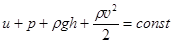 . (3.16)
. (3.16)
Здесь u = U| V – внутренняя энергия единичного объема. Очевидно, U = CVT = cV mT. Если выразить давление p из уравнения Клапейрона-Менделеева, p = nRT/V = rRT/M, выразить из уравнения (2.24) nR = Cp - CV и подставить, то первые два члена объединяются.
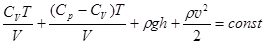 . (3.17)
. (3.17)
Тогда 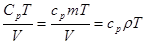 . (3.18)
. (3.18)
Подставляем в (3.17) и сокращаем на r.
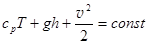 . Уравнение Бернулли для идеального газа (3.19)
. Уравнение Бернулли для идеального газа (3.19)
7. Скорость истечения идеального газа из баллона через малое отверстие. Ее вычисление имеет большое значение в технике реактивного движения и в космонавтике.
Пусть в баллоне при температуре T1 и под давлением p1 находится идеальный газ. Полагаем, что в стенке баллона имеется малое отверстие, через которое газ вытекает в горизонтальном направлении. Допущение о горизонтальности струи позволяет избавиться в уравнении Бернулли от члена gh, что не существенно для результата, но упрощает решение.
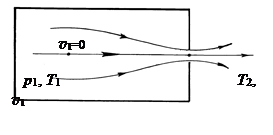 Выберем на горизонтальной линии тока, проходящей через отверстие, в глубине баллона, где течение мало заметно, точку 1, где линейную скорость v1 можно принять равной нулю, v1 = 0, и точку 2 в сечении отверстия (рис.9).
Выберем на горизонтальной линии тока, проходящей через отверстие, в глубине баллона, где течение мало заметно, точку 1, где линейную скорость v1 можно принять равной нулю, v1 = 0, и точку 2 в сечении отверстия (рис.9).
При этих условиях уравнение Бернулли для линии тока принимает вид:
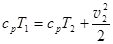 . (3.20)
. (3.20)
Отсюда выражаем скорость истечения газа 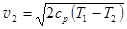 . (3.21)
. (3.21)
Если полагать процесс истечения адиабатным, что в большинстве случаев справедливо, то от температурного скачка T1 - T2, который трудно оценить, можно перейти к скачку давлений. Из формулы (3.10) 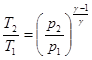 , Þ
, Þ 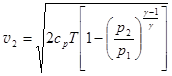 . (3.22)
. (3.22)
Скорость максимальна при истечении в пустоту при p2 = 0 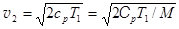 . (3.23)
. (3.23)
Чем меньше молярная масса газа M, тем больше скорость его истечения. Для молекул воды, образующихся в водородно-кислородном двигателе, скорость истечения при T1 = 1500 K и при условии, что Cp = 4R, составляет 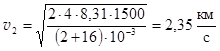 .
.
Дата добавления: 2020-05-20; просмотров: 1251;











