Основное уравнение кинетической теории газов

1. Кинетическая модель идеального газа.С точки зрения молекулярно-кинетической теории абсолютно идеальным является газ, представляющий собой систему из огромного числа материальных точек, то есть бесконечно малых частиц, не взаимодействующих между собой и не сталкивающихся друг с другом.

При таких допущениях частицы идеального газа должны считаться совершенно свободными. Это значит, что движутся они прямолинейно и равномерно от одного соударения со стенкой сосуда до другого. Каждая частица идеального газа ведет себя так, как будто других частиц вокруг нее нет.

Физические законы и следствия, которым идеальные газы подчиняются точно, справедливы с определенной погрешностью и для реальных газов.

2. Основное уравнение кинетической теории газов.Поскольку газ есть система из хаотически движущихся с разными скоростями молекул, то можно предположить, что давление газа на стенки сосуда есть результат множества соударений молекулы со стенками. Поэтому должна быть определенная количественная связь между средними параметрами движения молекул и величиной давления.

Впервые эту связь теоретически установил Рудольф Клаузиус в 1857 году. Рассмотрим два подхода к этой задаче.

а.Скорости молекул газа одинаковы по величине.Предположим сначала, что все молекулы газа одинаковы, каждая имеет массу m, двигаются они хаотично с одинаковыми по величине скоростями u. Направления скоростей равновероятны (гипотеза элементарного беспорядка). Газ находится в замкнутом сосуде.

Выделим часть стенки площадью S, нормальную оси x. Полагаем, что молекулы газа соударяются со стенкой абсолютно упруго.

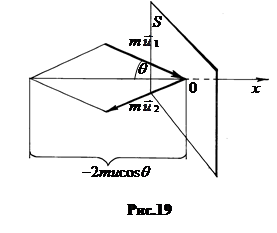Изменение импульса каждой молекулы при ударе 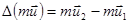в проекции на ось OX составляет -2mu cosq = -2mu_x (рис.19). Здесь u_x= u cosq - проекция на ось OX скорости молекулы до соударения, q - угол между вектором скорости 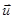и осью OX. Импульс силы со стороны молекулы на стенку 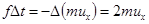, (7.1)

где Δt – продолжительность соударения молекулы со стенкой.

За время dt>>Dt о стенку ударится половина молекул слоя толщиной u_xdt, то есть 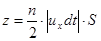. (7.2)

Здесь n – концентрация молекул газа.

Импульс силы со стороны всех z молекул на стенку есть 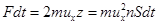. Отсюда давление идеального газа, молекулы которого двигаются с одинаковыми по величине скоростями, есть 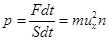. (7.3)

Давление газа пропорционально массе молекул m, их концентрации n и среднему квадрату проекции скорости движения молекул на нормаль к стенке .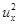

б. Скорости молекул газа различны по величине.В действительности скорости молекул газов разные не только по направлению, но и по величине.

Предположим, что газ состоит из нескольких групп молекул. Массы всех молекул одинаковы и равны m, а скорости молекул одинаковы по величине лишь в пределах групп. Пусть в группе 1 – скорости молекул 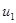, в группе 2 – скорости молекул 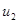,… в группе i скорости молекул .

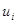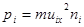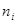Парциальное давление газа каждой группы определится также формулой (7.3): , где - концентрация молекул газа в i-той группе.

По закону Дальтона для парциальных давлений суммарное давление газа в целом есть сумма парциальных давлений, 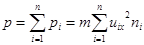_. (7.4)

Сумму можно представить так: 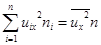, где n – концентрация всех молекул газа, а 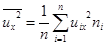- средний квадрат проекции скорости всех молекул.

Заметим, что число групп молекул в единице объема может достигать 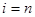. То есть каждая молекула может иметь отличную от других молекул скорость, так что число групп будет равно числу молекул. Итак, 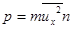. (7.5)

По сравнению с формулой (7.3) здесь входит средний квадрат проекции скорости.

Перейдем от проекции скорости 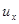к модулю скорости u. Вектор скорости любой молекулы можно представить как сумму составляющих по осям. 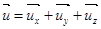, (7.6)

или 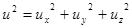. (7.7)

Направления скоростей равновероятны. Поэтому средние квадраты для системы с большим числом частиц одинаковы, 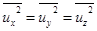. Тогда

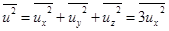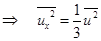, . (7.8)

Подставляем. .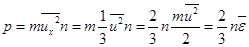

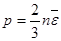. Основное уравнение кинетической теории газов (7.9)

Давление в газах пропорционально концентрации молекул n и их средней кинетической энергии 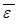хаотического поступательного движения.

3. Уравнение Клаузиуса.Формула (7.9) определяет макропараметр давление p как функцию двух микропараметров – концентрации молекул n и их средней кинетической энергии поступательного движения 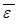. Чтобы вычислить какой либо микропараметр, нужно, чтобы в уравнении он был один, а все остальные были бы макропараметрами.

Умножим формулу (7.9) на объем V и сравним её с уравнением Клапейрона-Менделеева. 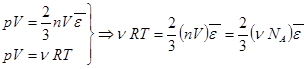. (7.10)

Здесь 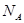- число Авогадро. Разделив уравнение на ν, получаем 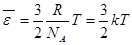. (7.11)

Отношение R/N_A=k называют постоянной Больцмана. Ввел ее в практику Макс Планк в 1900 году. Это одна из важнейших констант в физике. Ее современное значение (1978 год) k = (1,380622 ± 0,000044)×10^-23 Дж/К.

Формула (7.11) определяет среднюю кинетическую энергию поступательного движения одной молекулы идеального газа как функцию температуры газа T. Энергия пропорциональна абсолютной температуре газа.

Энергия молекулы, приходящаяся на 1 K, составляет 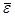=³/₂×1,38×10^-23 =2,07×10^-23 Дж.

Если подставить 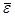=³/₂kT в основное уравнение кинетической теории газов, то получаем формулу, из которой можно вычислить концентрацию молекул газа n.

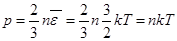. Уравнение Клаузиуса (7.12)

Вычислим концентрацию молекул воздуха при нормальных условиях.

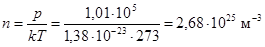. (Иоганн Лошмидт, 1865)

4. Среднеквадратичная скорость молекул находится из условия:

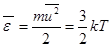. Отсюда 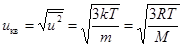. (7.13)

Здесь M – молярная масса газа.

Среднеквадратичная скорость 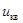- это скорость, средняя по кинетической энергии молекул. Например, для азота, М = 0,028 кг/моль, при T = 273 K

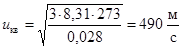. Для кислорода при той же температуре 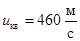, для водорода u_кв = 1800 м/с, для углекислого газа u_кв = 390 м/с. Чем больше молярная масса газа, тем меньше скорость движения его молекул. У хлора М = 0,071 кг/моль, u_кв = 270 м/с, у ртути М = 0,200 кг/моль, скорость движения ее атомов в парах u_кв = 180 м/с.

5. Температура T и давление p - статистические величины. Эти понятия применимы лишь к системам с огромным числом молекул, соизмеримым с числом Авогадро N_A = 6,022×10²³ моль^-1

Свойства газа как системы частиц не сводимы к свойствам отдельных молекул. Такая система проявляет новые качества и характеризуется новыми физическими величинами – давлением p и температурой T. Здесь проявляется диалектический закон перехода количества в качество. Свойства газов определяются усредненными параметрами молекул – средней кинетической энергией 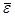, средней скоростью 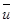, средним импульсом 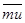. Средние величины находятся методами статистики. Раздел физики, методом исследования в котором является статистика, называется статистической физикой.

6. Изменение температуры газа в адиабатных процессах благодаря кинетической модели газа из эмпирического факта превращается в явление с наглядным механизмом.

Когда газ сжимается, его молекулы сталкиваются с приближающейся стенкой сосуда. Если скорость стенки u₀, то каждая ударившаяся упруго с ней молекула, двигавшаяся до удара со скоростью u, отскакивает от стенки со скоростью u + 2u₀ (См.: Механика, упругий удар шара со стенкой). Кинетическая энергия молекулы увеличивается с 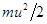до 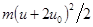. Температура газа растет.

Когда газ расширяется, молекулы ударяются с убегающей стенкой. Скорость молекул уменьшается на величину 2u₀, уменьшается соответственно их кинетическая энергия. Температура газа падает.

7. Броуновское движение.В 1827 г. английский ботаник Роберт Броун, наблюдая в усовершенствованный оптический микроскоп с большим увеличением микроорганизмы в воде, обнаружил, что невозможно получить резкое изображение этих микрообъектов. Оказалось, что микрочастицы, взвешенные в жидкости, находятся в состоянии непрерывного дрожания. Факт их реального дрожания подтверждался тем, что царапины и частицы меньших размеров на твердой подложке наблюдались вполне отчетливо. Позднее подобное дрожание, которое стали называть броуновским движением, обнаружили и в газах.

В этом явлении замечательно проявилась молекулярно-кинетическая структура вещества. Микрочастицы размером 0,1 ÷ 10 мкм находятся среди хаотично движущихся молекул жидкости или газа. Размер молекул примерно в 1000 раз меньше. Благодаря случайному распределению ударяющихся о частицу молекул сообщаемый ими импульс с какой-либо стороны оказывается больше. В результате возникает некоторая отличная от нуля равнодействующая сила, перемещающая частицу.

Интенсивность броуновского движения не ослабевает со временем и не зависит от химических свойств среды. Было замечено, что она тем больше, чем выше температура среды и чем меньше ее вязкость.

Теорию броуновского движения в рамках МКТ независимо друг от друга построили Альберт Эйнштейн и Мариан Смолуховский в 1905-906 г.г.

Оказалось, что в результате случайных толчков со стороны молекул броуновская частица дрейфует, удаляясь от исходной точки по закону

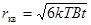. Формула Эйнштейна-Смолуховского (7.14)

Здесь 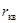- среднеквадратичное удаление частицы от исходного положения, k – постоянная Больцмана, T – абсолютная температура среды, t – продолжительность времени наблюдения, B – подвижность.

У частиц сферической формы B = 1ç6pha, (7.15)

где h – вязкость среды, a – радиус броуновской частицы.

Экспериментально проверили и подтвердили формулу Эйнштейна-Смолуховского Жан Перрен и независимо от него Теодор Сведберг в 1906-908 г.г. Вычисленные по результатам их измерений число Авогадро N_A и постоянная Больцмана k совпали со значениями, найденными другим путем.

Перрен работал с частицами эмульсии каучуковых смол в воде (гуммигут) размером около 1 мкм и увеличением микроскопа около 3000 крат. Интервалы времени составляли около 30 с. Соединяя прямыми линиями последовательные положения частиц, он получил ломаную со случайными значениями длин отрезков и их направлений. Расчеты показывают, что в 1 с броуновская частица испытывает до 10¹⁴ молекулярных толчков. Поэтому, уменьшение интервала времени вплоть до 10^-14 с не превращает ломаную линию в гладкую кривую. Гладкими кривыми является лишь отрезки, на которых броуновская частица движется от одного толчка до другого.

Броуновское движение дает возможность установить тот минимальный объем, в котором вещество еще можно рассматривать как сплошную бесструктурную среду. Дрожание частиц становится заметным, начиная с радиуса частиц a » 10 мкм. Это свидетельствует о том, что начиная с объема a³ » 10^-15 м³ вещество уже проявляет свою дискретную структуру.

Поскольку броуновская частица находится в тепловом равновесии с окружающей средой, то ее средняя кинетическая энергия такая же, как и у молекул среды. Поэтому среднеквадратичная скорость частицы (средняя по энергии), взвешенной в газе, находится по формуле 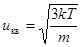, (7.16)

где m – масса броуновской частицы.